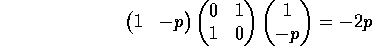Existence of Line Bundles on K3-surfaces
Jörg Winkelmann
We stated (Sct. 7.13., p. 129)
"it is possible that a compact complex manifold does not admit any
non-trivial
line bundle, namely this happens for K3-surfaces of algebraic
dimension zero."
In fact, this happens for a generic K3-surface of
algebraic dimension zero, but not for every one.
There are K3-surfaces of algebraic dimension zero with
some non-trivial line bundles.
(1) A K3-surface X has algebraic dimension zero if and only if
the intersection product on Pic(X) is negative definit.
Proof: K3-Surfaces have trivial canonical bundle.
Hence Riemann-Roch yields X(D)=(1/2)D.D + 2
and X(D)
 h0(D)+h2(D) = h0(D) + h0(-D)
for every line bundle D.
If L is a non-trivial line bundle with L.L
h0(D)+h2(D) = h0(D) + h0(-D)
for every line bundle D.
If L is a non-trivial line bundle with L.L
 0,
this implies that dim H0(L)
0,
this implies that dim H0(L)
 2 or
dim H0(L-1)
2 or
dim H0(L-1)
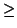 2.
Thus there is a line bundle with two linearly independent sections
and therefore a non-constant meromorphic function.
2.
Thus there is a line bundle with two linearly independent sections
and therefore a non-constant meromorphic function.
Conversely, if the algebraic dimension is two or one, then
there exists a curve which is ample resp. the fiber of the
algebraic reduction. Now C.C >0 for ample curves and C.C=0 for
fibers of surjective holomorphic maps from a surface to a curve.
(2)
All K3-surfaces are diffeomorphic, hence H2(X,Z) with cup-product
is isomorphic to a fixed Z-module of rank 22 with fixed bilinear
product (This Z-module is called L=LZ in [BPV], Ch.VIII).
This bilinear form is non degenerate and of signature (19,3)
(19 negative, 3 positive). For every K3-surface, there is
a non-zero holomorphic two-form which yields an element w in LC
( LC= tensor product of LZ with C over Z)
such that
(w,w)=0 and (w,\bar w)>0. (*)
Conversely, for every w in LC fulfilling (*) there exists a
corresponding K3-surface (Torelli-Theorem, [BPV], Ch.VIII, (14.2) ).
Now, the wedge-product of any (1,1)-form with w or \bar w is zero.
Hence H1,1(X) is the orthogonal complement of
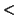 w,\bar w
w,\bar w
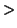 in H2(X,C)=LC. Let w=u+iv denote the decomposition of w into
real and imaginary part. Then (*) is equivalent to:
in H2(X,C)=LC. Let w=u+iv denote the decomposition of w into
real and imaginary part. Then (*) is equivalent to:
(u,u)=(v,v)>0 and (u,v)=0 (**)
Thus
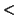 u,v
u,v
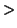 is a real two dimensional subspace of LR such that
the intersection product is positive definit.
Conversely, if H is a real two-dimensional subvectorspace of LR
on which the product is positive definit, one can choose u,v fulfilling
(**).
Together with the Torelli theorem quoted above this implies:
Let V be a subvectorspace of LR of real codimension two and let
H denote its orthogonal complement.
Then there exists a K3-surface X such that H1,1(X)=V
if and only if the product on H is positive definit.
is a real two dimensional subspace of LR such that
the intersection product is positive definit.
Conversely, if H is a real two-dimensional subvectorspace of LR
on which the product is positive definit, one can choose u,v fulfilling
(**).
Together with the Torelli theorem quoted above this implies:
Let V be a subvectorspace of LR of real codimension two and let
H denote its orthogonal complement.
Then there exists a K3-surface X such that H1,1(X)=V
if and only if the product on H is positive definit.
(3) We also need (see [BPV], Ch, IV, thm. (2.12) ):
The image of Pic(X) in H2(X) is precisely the intersection
of H2(X,Z) and H1,1(X).
(4)
Let x be an element in LZ such that (x,x)<0.
Since the signature is (19,3), there is a subvectorspace V of LR
of codimension two with a positive definit orthogonal complement.
Let W denote the set of all subvectorspaces V of LR of codimension
two with positiv definit orthogonal complement such that x is in V.
This set W is an open set in some algebraic subvariety of some
Grassmannian. Now, for every y in LZ, the set of all V in W with
W containing y defines a subset Sy of W.
It is clear that this set Sy is nowhere dense in W.
Everything here is at least real analytic (or sub/semi-algebraic
if you prefer), hence it follows that a countable union of such Sy
can not be the whole W.
For this reason there exists a subvectorspace V of LR
of codimension two, containing x
such that the orthogonal complement is positive definit
and V does not contain any element y in LZ with
(y,y)
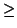 0.
Thus the intersection of V with LZ is non-trivial and the
product on this intersection is negativ definit.
0.
Thus the intersection of V with LZ is non-trivial and the
product on this intersection is negativ definit.
It follows that the corresponding K3-surface has algebraic
dimension zero, but does admit non-trivial line bundles.
(5) Note that x in LZ was arbitrary except for the condition
x,x<0, and that, by similar arguments, we may require that
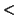 x
x
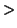 Z
is exactly Pic(X) if x is primitive, i.e., if there does
not exist any y in LZ with ny=x for some natural number n>1.
The structure of LZ is described in detail in [BPV].
In particular, it contains as a direct summand a
hyperbolic Z-plane, i.e. a Z2 with
the product given by the matrix
Z
is exactly Pic(X) if x is primitive, i.e., if there does
not exist any y in LZ with ny=x for some natural number n>1.
The structure of LZ is described in detail in [BPV].
In particular, it contains as a direct summand a
hyperbolic Z-plane, i.e. a Z2 with
the product given by the matrix
 .
.
(This direct summand is called H in [BPV]).
Now let p be a natural number.
Then
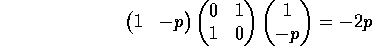
Thus there is a primitive element x in LZ with (x,x)= -2p.
It follows, by the arguments used above, that there exists
a K3-surface X ( of algebraic dimension zero)
such that Pic(X) is generated by a single element x with (x,x)=-2p.
Clearly, Pic(X) is not generated by (-2)-curves.
Actually, [BPV],Ch,VIII, Prop.3.7 now implies that this surface
contains no curves.
Thus there exists an example of a K3-surface of algebraic dimension
zero which does not contain any curve, but which nevertheless
admits a non-trivial line bundle.
[BPV] : Barth, Peters, van de Ven: Complex Surfaces.
Click here
for remakrs, comments, etc.
Last modification:
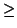 h0(D)+h2(D) = h0(D) + h0(-D)
for every line bundle D.
If L is a non-trivial line bundle with L.L
h0(D)+h2(D) = h0(D) + h0(-D)
for every line bundle D.
If L is a non-trivial line bundle with L.L
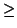 0,
this implies that dim H0(L)
0,
this implies that dim H0(L)
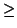 2 or
dim H0(L-1)
2 or
dim H0(L-1)
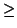 2.
Thus there is a line bundle with two linearly independent sections
and therefore a non-constant meromorphic function.
2.
Thus there is a line bundle with two linearly independent sections
and therefore a non-constant meromorphic function.
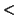 w,\bar w
w,\bar w
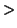 in H2(X,C)=LC. Let w=u+iv denote the decomposition of w into
real and imaginary part. Then (*) is equivalent to:
in H2(X,C)=LC. Let w=u+iv denote the decomposition of w into
real and imaginary part. Then (*) is equivalent to:
 .
.