Semantische Bäume in LP

Im Grundkurs haben wir die Methode der semantischen Bäume oder des Baumkalküls als Beweisverfahren kennengelernt.

Gegeben eine beliebige aussagenlogische Formel \(A\) stellt sich die Frage, ob diese allgemeingültig ist. Die Beweismethode der semantischen Bäume geht hier indirekt vor.

Semantische Bäume zur Überprüfung der Allgemeingültigkeit einer gegebenen Formel

Wir wiederholen zunächst die Methode für die klassische Logik:

Wir nehmen zunächst an, \(A\) wäre falsch. Dazu schreiben wir zunächst \(\neg A\) ganz oben in die sogenannte “Wurzel” unseres Baumes.
Wir analysieren dann die gegebene Situation mit der Hilfe von Ableitungsregeln.
- Etwa: falls \(A = B \vee C\) falsch ist, so müssen sowohl \(B\) als auch \(C\) falsch sein. Die motiviert die Regel:
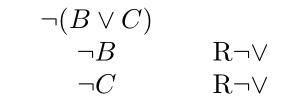
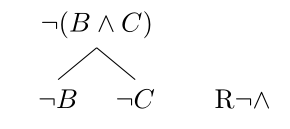
- Oder: falls \(A = B \wedge C\) falsch ist, so muss mindestens eine der beiden Komponenten der Konjunktion, \(B\) oder \(C\) falsch sein – wir können nicht im Allgemeinen wissen welcher der Fälle. Wir müssen also zwei Möglichkeiten in Betracht ziehen, was eine Split-Regel motiviert:
- So gibt es für jeden Junktor eine entsprechende Regel, die es erlaubt die gegebene Formel zu analysieren.
Durch die Anwendung unserer Regeln ergibt sich so ein Baum, der in der seltsamen Welt der Logik jedoch von oben nach unten wächst. Hier ein Beispiel:

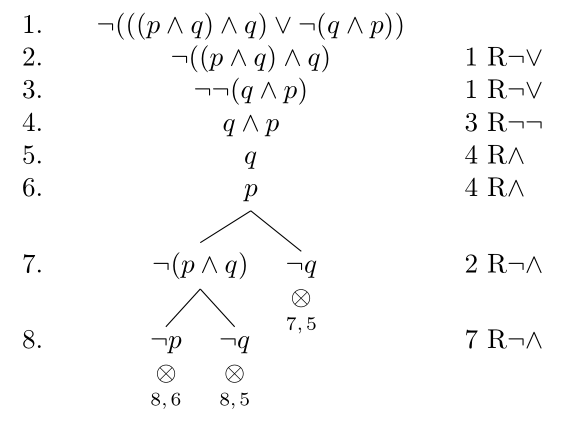Die Zeilennummern auf der linken Seite geben wir an, um einen leichteren Überblick zu schaffen. Auf der rechten Seite sind jeweils die Regeln angegeben, die benutzt wurden und die entsprechende Zeile auf die sie angewendet wurden. Wir haben folgenden zusätzliche Regeln benutzt:
Hinter den Verzweigungen verbergen sich die jeweiligen Möglichkeiten, unsere gegebene Formel – im Beispiel \(\neg (((p \wedge q) \wedge q) \vee \neg( q \wedge p))\) – als wahr zu interpretieren. Oder, entsprechend die nicht-negierte Formel – im Beispiel \((((p \wedge q) \wedge q) \vee \neg( q \wedge p))\) – falsch zu interpretieren.
Sollten sich – wie im Beispiel – alle Versuche so eine Interpretation zu finden als widersprüchlich herausstellen, so gibt es keine wahre Interpretation der negierten Formel. D.h. dann gibt es keine Möglichkeit, dass die (nicht negierte) Formel falsch ist. Somit muss sie in allen Interpretation den Wahrheitswert 1 erhalten und somit allgemeingültig sein.
Ein Ast eines Baumes wird mit einem \(\times\) markiert und heißt geschlossen, falls sich darauf eine Formel \(B\) und ihre Negation \(\neg B\) befindet.
Falls keine Regeln mehr auf einen Ast angewendet werden können (ohne bereits auf dem Ast befindliche Formeln zu erzeugen) oder falls ein Ast geschlossen ist, so ist dieser vollständig. Ein Baum ist vollständig, falls alle seiner Äste vollständig sind.
Eine Formel \(A\) gilt als bewiesen, falls es einen geschlossenen Baum gibt mit \(\neg A\) in der Wurzel: d.h. ein Baum dessen Äste alle mit \(\times\) markiert, also geschlossen sind.
In diesem Sinne ist das Beweisverfahren ein Widerlegungsverfahren: wir gehen zunächst von der Annahme aus \(A\) wäre falsch (also \(\neg A\) gelte), um diese Annahme unter weiterer Analyse (d.h. der Anwendung der Ableitungsregeln) zum Widerspruch zu führen.
Falls es einen vollständigen Baum mit \(\neg A\) in der Wurzel gibt, für den mindestens ein Ast offen ist (also nicht geschlossen), so ist \(A\) nicht beweisbar. In dieser Weise widerlegen wir, dass \(A\) allgemeingültig ist. Der offene vollständige Ast gibt uns Informationen darüber, wie eine Interpretation aussieht, in der \(\neg A\) gilt und deshalb \(A\) nicht gilt. Hier ein Beispiel:

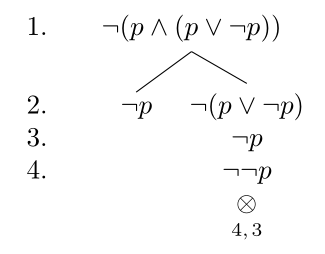Der linke Zweig ist vollständig und offen. Eine Interpretation in der \(\neg (p \wedge (p \vee \neg p))\) gilt ist durch die Belegung gegeben, die dem Atom \(p\) den Wahrheitswert 0 zuweist.

Wie wir im Seminar gesehen haben, haben LP und die klassische Logik diesselben Tautologien. Zudem wissen wir aus dem Grundkurs, dass das obige Beweisverfahren vollständig und korrekt ist: d.h. die beweisbaren Formeln stimmen genau mit den Tautologien überein. Daraus ergibt sich sogleich, dass obige Beweismethode auch zum Nachweis von Tautologien für LP benutzt werden kann.

Die Beweismethode zum Nachweis logischer Konsequenzen

Aus dem Grundkurs wissen wir, dass obiges Beweisverfahren im Kontext der klassischen Logik auch zum Nachweis logischer Konsequenzen benutzt werden kann. Um zu Überprüfen, ob \(A\) aus der Prämissenmenge \({A_1, \ldots, A_n}\) folgt, müssen wir \(\neg A\) in der Wurzel des Baumes einfügen, und dürfen zusätzlich Prämissen in den Baum (nicht-negiert!) einführen. Die Grundidee ist wieder die der Widerlegung: wir gehen zunächst davon aus, dass \(A\) falsch ist, aber die Prämissen wahr sind. Falls in der weiteren Analyse sich herausstellt, dass es keine Möglichkeit gibt unsere gegebenen Formeln widerspruchsfrei unter diesen Annahmen zu interpretieren, so kann es kein Modell der Prämissen geben in dem \(A\) falsch ist. Somit ist \(A\) in allen Modellen der Prämissen wahr und damit eine Konsequenz der Prämissen.

Hier ist ein Beispiel:

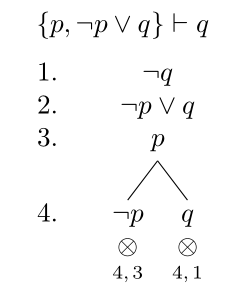
In der Wurzel finden wir zunächst unsere negierte Formel, die als Konsequenz nachgewiesen werden soll. In Zeilen 2 und 3 finden wir (nicht-negiert) die beiden Prämissen. Der Baum schließt, also ist \(q\) eine Konsequenz unserer beiden Prämissen.

Annotierte Bäume in der klassischen Logik

Diese Verfahren lässt sich nicht direkt auf LP übertragen: wie wir aus dem Seminar wissen gilt der Disjunktive Syllogismus nicht in LP. Obiger Beweis ist also nicht zulässig in LP. Das Problem ist, dass das Vorkommnis einer Formel und ihrer Negation auf einem Ast in LP (!) nicht ausreicht, um nachzuweisen, dass es kein Modell der Formeln auf dem entsprechenden Ast gibt! Etwa gibt es sehr wohl ein Modell der beiden Äste im obigen Beispiel in LP: für den linken Ast etwa müssen wir \(p\) lediglich mit \(i\) belegen. Wie wir aus der letzten Übung wissen, geht das Problem noch tiefer: für jede Menge von aussagenlogischen Formeln gibt es in LP ein Modell!

Wir müssen also etwas tiefer in unsere Trickkiste greifen und es reicht nicht aus lediglich Formeln im Baum zu listen. Stattdessen müssen wir explizit deren Wahrheitswerte erwähnen, denn, was niemals passieren kann ist, dass eine Formel zwei verschiedene Wahrheitswerte erhält in ein und derselben Interpretation.

Hierfür benötigen wir annotierte Bäume. Wir zeigen zunächst, wie das Verfahren in der klassischen Logik funktionert. Dazu wandeln wir obigen Baum in einen annotierten Baum um:

Formeln sind nun mit Wahrheitswerten annotiert. In der Wurzel des Baumes setzen wir \(q\) als falsch an: “\(0:q\)”. Dann führen wir die beiden Prämissen als wahr ein (Zeilen 2 und 3). Dann wenden wir die positive Regel für Disjunktion an:

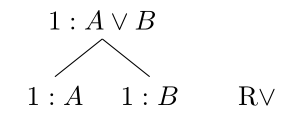
In Zeile 4, links, wird ausserdem die positive Regel für Negation angewandt:

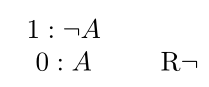
Wie ihr wahrscheinlich schon richtig vermutet habt, sehen die negativen Varianten obiger Regeln wie folgt aus:

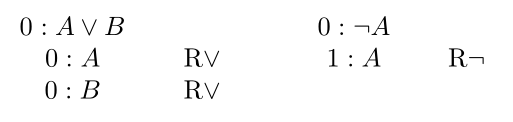
Der Widerspruch oben ergibt sich im linken Ast deshalb weil der Analyse zufolge \(p\) sowohl wahr (Zeile 3) also auch falsch (Zeile 5) sein soll – was natürlich nicht möglich ist. Ähnlich sollte auf der rechten Seite \(q\) sowohl wahr (Zeile 4) als auch falsch (Zeile 1) sein – was wieder nicht möglich ist. Ein Ast schließt also genau dann wenn sich sowohl \(1:A\) als auch \(0:A\) auf dem Ast befinden für eine Formel \(A\).

Wir führen nun die restlichen Regeln für annotierte Bäume in der klassischen Logik an. Zunächst für Konjunktion:

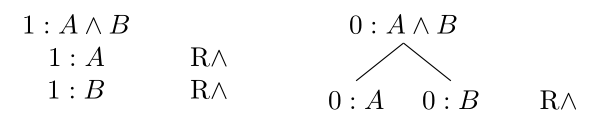
Und nun für Implikation:

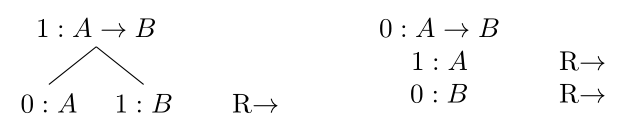
Dieses Verfahren lässt sich ähnlich auch auf LP anwenden. Jedoch müssen wir berücksichtigen, dass wir in LP mit drei Wahrheitswerten arbeiten.

Annotierte Bäume in LP

Angenommen, wir wollen zeigen, dass in LP \(B\) aus \({A_{1}, \ldots, A_n}\) folgt. Im Sinne des Baumverfahrens wollen wir also widerlegen, dass es ein Modell gibt in dem \(B\) falsch ist und in dem gleichzeitig die Prämissen gelten. Das heißt, die Prämissen haben in einem solchen Modell jeweils entweder den Wert 1 oder den Wert \(i\), während \(B\) den Wert 0 hat. Um nicht für jede Prämisse Fallunterscheidungen treffen zu müssen und entsprechend, um nicht beim Einfügen der Prämissen den Baum spalten zu müssen, benutzen wir die Notation: \([1,i]: A_i\) um anzugeben, dass \(A_i\) einen der beiden Wahrheitswerte 1 oder \(i\) hat. Hier ist ein erstes Beispiel für einen Beweis:

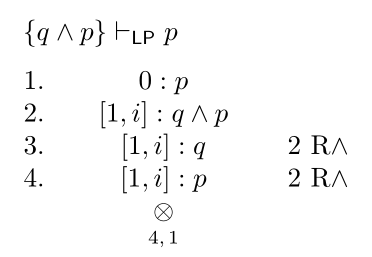
Der Widerspruch ergibt sich hier darin, dass es kein Modell geben kann, in dem \(p\) sowohl 0 (Zeile 1) als auch 1 oder \(i\) (Zeile 4) ist.

Die Regeln für Negation \(R{\neg}\) sind die folgenden:

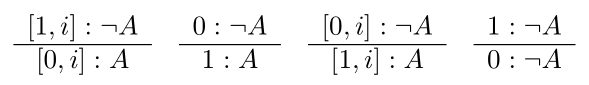
Um zu sehen, dass diese Tabellen adäquat sind, erinnere man sich an die Tabelle für die parakonsistente Negation:

	\(\neg\)
0	1
i	i
1	0

Etwa in der Regel ganz links müssen wir Zeilen 1 und 2 in der Wahrheitstabelle betrachten: falls \(\neg A\) den Wert \(1\) oder \(i\) hat, so muss \(A\) entweder 0 oder \(i\) sein. Ähnlich in anderen Fällen.

Andere Regeln sind:

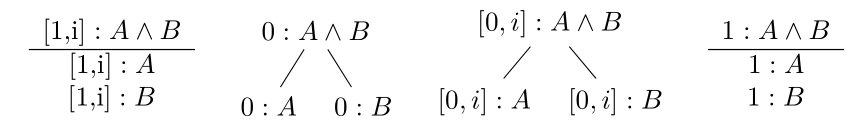
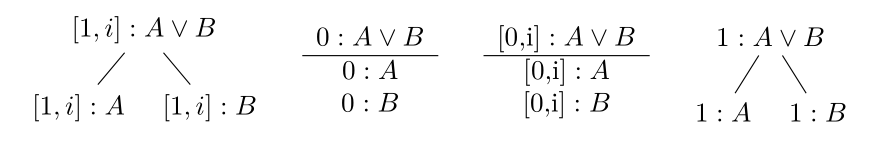
Ein Ast gilt in LP-Bäumen als geschlossen (und wird mit \(\times\) markiert), falls einer der folgenden Fälle eintritt:

\(0: A\)	und	\([1,i] :A\)
\([0,i] : A\)	und	\(1 : A\)
\(0:A\)	und	\(1 : A\)

Beispiele

Der folgende Baum beweist, dass \(p\) aus \(p \wedge \neg p\) in LP folgt:

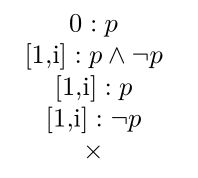
Der folgende Baum zeigt, dass \(q\) nicht aus \(p\) und \(\neg p \vee q\) in LP folgt, da nicht alle Äste schließen.

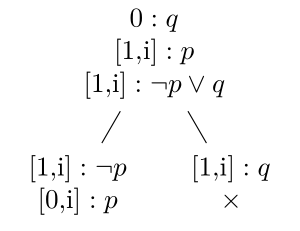
Beachte, dass der offene Ast Aufschluss darüber gibt, wie ein Modell aussieht in dem \(q\) falsch ist, aber die beiden Prämissen wahr: \(p\) muss widersprüchlich sein.

Updates

[2018-11-09 Fri 11:56] Korrektur: negative Regel für \(\vee\) in der klassischen Logik und Beispiel 1 waren fehlerhaft. Danke an Sarah Blenk für die Hinweise :-)