Sitzung 6: Vagheit
Vagheit wird oft im Kontext des sogenannten Sorites Paradoxes diskutiert. Es gibt zahlreiche Varianten desselben, die sich weniger in der logischen Struktur als vielmehr im konkreten Inhalt unterscheiden. Diese basieren jeweils auf einem spezifischen vagen Prädikat, wie etwa: “… hat eine Glatze”, “… ist grün”, “… ist ein Haufen”, “… ist ein Kind”, etc. Solche Prädikate erlauben es uns, ob konkret oder als Gedankenexperiment, eine Reihe von Individuen aufzustellen,
- so dass diese das jeweilige Prädikat in abnehmender Weise erfüllen, oder
- bei denen es für kompetente Sprecher zunehmend schwierig wird, zu sagen, ob das jeweilige Prädikat zutrifft, oder
- bei denen kompetente Sprecher mehr und mehr in der Zuschreibung des Prädikats divergieren.
Man stelle sich etwa vor,
- eine Sequenz von Farbmustern von rot bis orange, bei der sich Nachbarn in kaum oder nicht wahrnehmbarer Weise unterscheiden;
- ein Haufen von feinen Körnern, von dem nach und nach ein Körnchen entfernt wird, solange bis kein Körnchen mehr übrig bleibt;
- eine Sequenz von Männern, beginnend links mit einem Mann ohne jegliches Haar auf dem Kopf, und dann jeweils ein Mann mit einem Haar mehr als der Vorgänger, bis zu einem Mann ganz rechts mit dichtem Haar.1
Wir sprechen bei solchen Szenarion von einem Paradox, da, wenn wir folgende recht einleuchtende Prinzipien akzeptieren, unsere logischen Schlüsse in einen Widerspruch führen:
- Der Mann ganz links hat eine Glatze: \(g_0\).
- Wenn ein beliebigen Mann in unserer Reihe eine Glatze hat, dann hat sein Nachfolger, der ja nur ein Haar mehr hat, auch eine Glatze: \(g_i \rightarrow g_{i+1}\).
- Der Mann ganz rechts (der \(n\)-te Mann in unserer Reihe) hat keine Glatze: \(\neg g_n\).
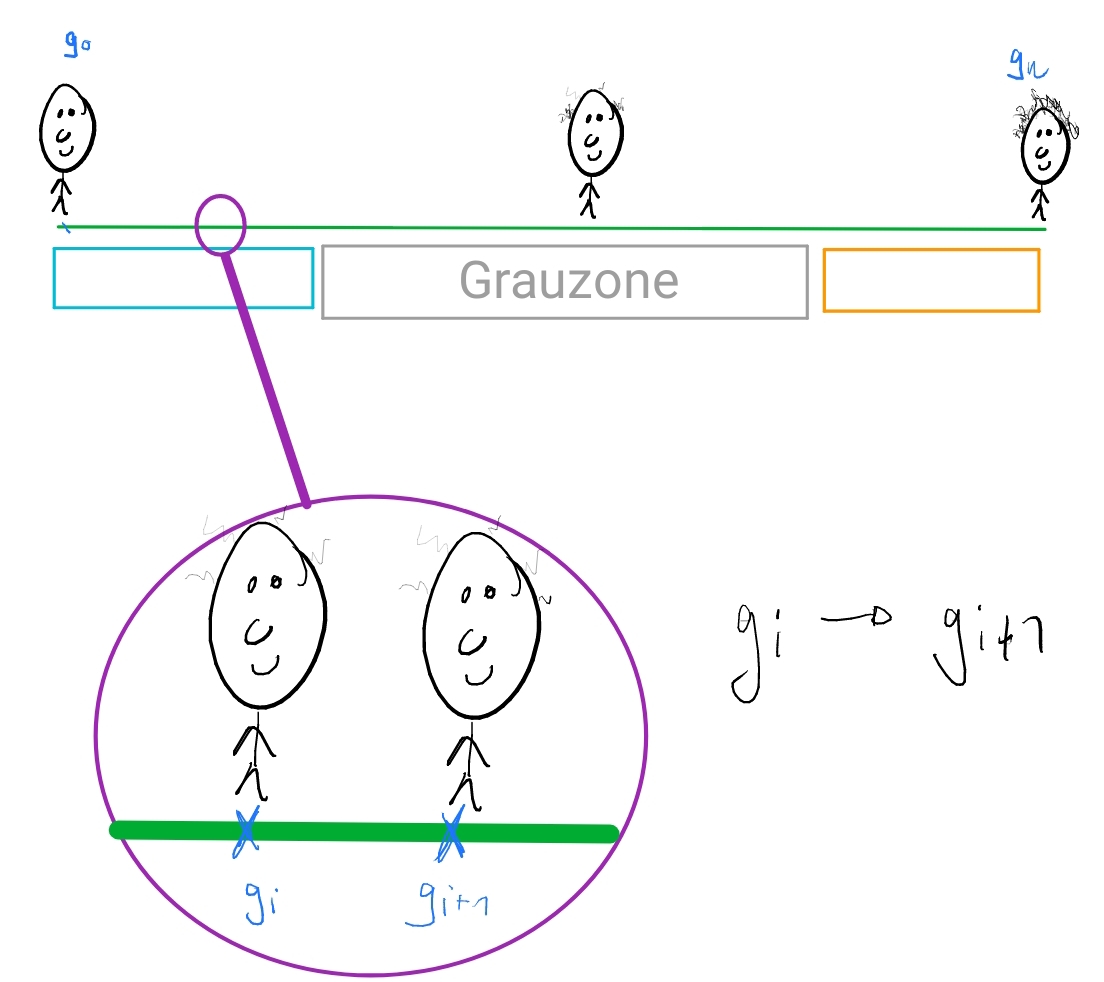
Prämissen 1 und 3 scheinen völlig unkontrovers. Lediglich Prämisse 2 scheint nicht ganz trivial oder selbstevident zu sein. Die These wird üblicherweise aufgrund des sogenannten Toleranzprinzips vertreten:
Suppose that two objects \(a\), \(a^{\prime}\) in the field of \(P\) differ only marginally in the relevant respect (on which \(P\) is tolerant). Then if one competently judges \(a\) to have \(P\), then she cannot competently judge \(a^{\prime}\) in any other manner.
Shapiro, 2006, p. 8 (vgl. auch Wright, 1975, p. 334.)2
Tolerance. If \(a\) and \(b\) are very close in \(F\)-relevant respects, then ‘Fa’ and ‘Fb’ are identical in respect of truth.
Smith, 2008, p. 160
Da sich in den Fällen \(g_i\) und \(g_{i+1}\) unsere beiden potentiell Glatzköpfigen nur minimal (etwa um ein Haar) voneinander unterscheiden sollten sie sich hinsichtlich der Zuschreibung des Prädikats “… hat Glatze” auch nicht unterscheiden.
Wenden wir nun Modus Ponen wiederholt in unserer Situation an,
| Prämisse 1 | Prämisse 2 | Schluss |
|---|---|---|
| \(g_0\) | \(g_0\rightarrow g_1\) | \(g_1\) |
| \(g_1\) | \(g_1\rightarrow g_2\) | \(g_2\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(g_{n-1}\) | \(g_{n-1}\rightarrow g_n\) | \(g_{n}\) |
so kommen wir zum Schluss, dass \(g_{n}\), was \(\neg g_n\) widerspricht.
Der Begriff der Vagheit stellt uns vor verschiedene Herausforderungen:
- Lassen sich Szenarien wie das Sorites Paradox logisch modellieren, ohne Anlass zu kontra-intuitiven Resultaten zu geben?
- Können wir das 2-wertige Bild der klassischen Logik aufrecht erhalten, dem gemäß jede Aussage \(g_i\) entweder den Wahrheitswert 0 oder den Wahrheitswert 1 hat (d.h. weder beide noch keinen)?
- Gibt es Cut-Off Punkt in der Realität oder bzgl. des korrekten Sprachgebrauchs, an denen sich Wahrheitswertzuschreibungen von \(g_i\) und \(g_{i+1}\) ändern. Wenn ja, wo sind diese, sind diese wissbar, wie entstehen sie etwa als Produkt unserer (kompetenten) Sprachpraxis? Sind solche Cut-Off Punkte kontextuell gegeben? Sollen wir nicht eher von Cut-Off Zonen ausgehen die selbst vage sind? etc.
Im Seminar haben wir einen kurzen Überblick zu zentralen philosophischen Positionen und logischen Modellen zur Vagheit gegeben.
Epistemizismus
Der Epistemizismus geht davon aus, dass es einen strikten Cut-Off Punkt \(i\) in der Realität gibt, für den gilt \(g_i\) aber \(\neg g_{i+1}\). Dieser Cut-Off Punkt ist (selbst kompetenten) Sprachanwendern jedoch nicht zugänglich: genauer, wir können nicht wissen, wo er sich genau aufhält.
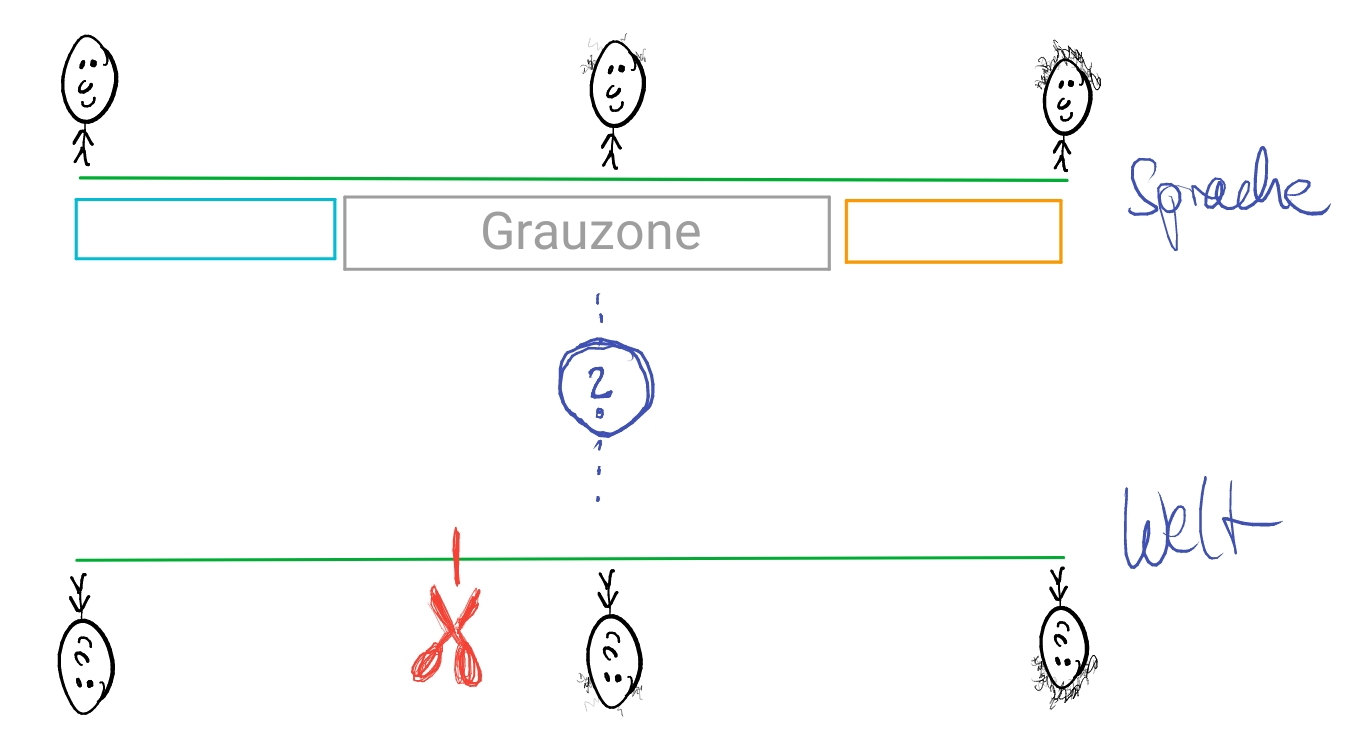
Dieser Ansatz wurde vor allem deshalb kritisiert, da er eine Kluft zwischen kompetenter Sprachanwendung und der Realität aufmacht. Vielfach wird von sprachphilosophischer Seite her argumentiert, dass der Sprachgebrauch kompetenter Sprecher eng mit der Frage der Wahrheitbedingungen von Aussagen zusammenhängt. Etwa Shapiro spricht von einem “truism that the competent users of a language determine the meaning of its words and its phrases” (Shapiro, 2006, p. 5). Ähnlich, McGee und McLaughlin argumentieren:
… to say that an object \(a\) is definitely an \(F\) means that the thoughts and practices of speakers of the language determine conditions of application for […] \(F\), and the facts about \(a\) determine that these conditions are met.
McGee and McLaughlin, 1994, §2
Smith bringt diesen Standpunkt wie folgt auf den Punkt:
The claim \(Pa\) is true if and only if most competent speakers would confidently assent if presented with \(a\) in normal conditions and asked whether it was \(P\), and is false if and only if most competent speakers would confidently dissent if presented with \(a\) in normal conditions and asked whether it was \(P\).
Smith, 2009, p.37
Beachte das “if and only if”: kompententen Sprechern ist es für Männer links und rechts vom Cut-Off Punkt \(i\) nicht möglich, mit Sicherheit zu sagen, ob sie eine Glatze haben, oder nicht, weil sie aus prinzipiellen Gründen (mehr dazu unten) nicht wissen können, wo sich der Cut-Off Punkt genau befindet. Manche werden also behaupten \(\neg g_i\), manche \(g_{i+1}\), manche werden sich der Stimme enthalten, etc. Dennoch gilt \(g_i\) während \(\neg g_{i+1}\). Das heißt, das von Smith formulierte Bikonditional hält nicht im Epistemizismus. Der Cut-Off Punkt hat eine scheinbar myseriöse Existenz, die sich unserer Erkenntnis radikal entzieht.
Die Vagheit findet sich also im Epistemizismus in der Unwissenheit der Sprecher begründet und weniger in einer Indeterminiertheit der Sprache hinsichtlich ihrer Bedeutung. Beachte dazu, dass hier die Extensions von Prädikaten wie “… hat eine Glatze” klassische determiniert ist, so dass jede beliebige Kopfbehaarung entweder darunter fällt oder nicht. Dies ist im Kontrast zu vielen anderen Ansätzen, wie etwa Peirces Definition aus dem Jahre 1902:
A proposition is vague when there are possible states of things concerning which it is intrinsically uncertain whether, had they been contemplated by the speaker, he would have regarded them as excluded or allowed by the proposition. By intrinsically uncertain we mean not uncertain in consequence of any ignorance of the interpreter, but because the speaker’s habits of language were indeterminate.
Charles Sanders Peirce 1902 (Dictionary of Philosophy and Psychology), p. 748, meine Hervorhebungen
Wie erklärt der Epistemizist, dass wir um den Cut-Off Punkt nicht wissen können? Hier kommt das erkenntnistheoretische Prinzip des Margin of Error zum Tragen. Smith formuliert dies wie folgt:
(M[argin of] E[rror]) “S knows that P” is true in a situation T only if P is true in situations that are sufficiently similar to T.
Eine offensichtliche Frage ist natürlich, was es heißt, dass eine Situation “sufficiently similar” ist. Man nehme an \(S\) hat ihren Erkenntniskandidaten \(P\) durch eine bestimmte Methode \(M\) gewonnen, etwa durch Wahrnehmung. Eine ausreichend ähnliche Situation wäre dann etwa eine Situtation, die relativ zu \(M\) für \(S\) (nahezu?) ununterscheidbar ist.
Sagen wir, im Kontext des Sorites Paradoxes, \(S\) wird konfrontiert mit dem \(i\)ten Farbmuster, wobei \(i\) unser Cut-Off Punkt ist, und sie ist der richtigen Überzeugung: “P = Diese Farbe ist noch unterhalb des Cut-Off Punktes und also solche gelb.” Alternativ hätten wir sie mit dem Farbmuster \(k+1\) konfrontieren können, ein für sie ununterscheidbares Farbmuster. In dieser, ausreichend ähnlichen Situtation ist \(P\) jedoch nicht wahr. Dem Margin of Error Prinzip zufolge kann \(S\) also nicht um \(P\) wissen. Da \(S\) dementsprechend nicht in der Lage ist, um die korrekte Klassifizierung von Grenzfällen als vor und nach dem Cut-Off Punkt zu wissen, scheint es auf der Hand zu liegen, dass \(S\) um den Ort des Cut-Off Punkts auch nicht wissen kann.3
Im Seminar haben wir kurz auch das sogenannte Gettier Problem in der Erkenntnistheorie diskutiert (etwa in der Version von Kripke) und festgestellt, dass ähnlich kontrafaktische Prinzipien von Epistemologen festgelegt wurden, um Fälle von Nicht-Wissen, die wahre und gerechtfertigte Überzeugungen sind zu charakterisieren (etwa von Dretske (1971) und Nozick (1981)).
Abschließend bleibt zu bemerken, dass eine der größten Herausforderungen an den Epistemizismus die Frage ist, welcher Mechanismus im Zusammenspiel von Sprache und Welt den strikten Cut-Off Punkt in der Realität etabliert.
Aller guten Dinge sind 3
In diesem Ansatz wird das 2-Wertigkeitsprinzip der klassischen Logik aufgegeben. In der von uns diskutierten Spielart, geht man davon aus, dass sich gewisse Aussagen im Graubereich von Sorites-Reihen der Wahrheitswertzuweisung entziehen und sogenannte Wahrheitswertlücken aufweisen. In der Logik kann man das in dreierlei Weisen realisieren:
- man arbeitet mit einem nicht-designierten Hilfswert \(u\) (etwa für “unbestimmt”), so dass Belegungen jedem Atom einen der drei Werte \(1\), \(0\), oder \(u\) zuweisen. Meist wird dann vereinfachenderweise auch von dem “Wahrheitswert” \(u\) gesprochen.
- man arbeitet mit Belegungen, die Atome mit Mengen von Wahrheitswerten assoziieren: in unserem Fall mit \({1}\) für wahr, \({0}\) für falsch, oder \(\emptyset\) für eine Lücke. (Im parakonsistenten Bereich hätten wir auch noch \({0,1}\) für sowohl wahr als auch falsch.)
- man arbeitet mit partiellen Belegungen. Diese assoziieren nicht alle Atome mit den Werten 0 oder 1, sondern nur manche (die “klaren” Fälle).
Wir werden zunächst wahrheitsfunktionale, mehrwertige Logiken besprechen und Ansatz 1 berücksichtigen. Im Falle des Supervaluationismus (siehe unten) werden wir mit Ansatz 3 arbeiten.
Im 3-wertigen Ansatz gehen wir von einer tripartiten Teilung unseres Glatzen-Sorites aus:
- klare Fälle von Glatzen
- klare Fälle von Nicht-Glatzen
- eine Grauzone, in der kompetenten Sprechern eine Entscheidung schwer fällt.
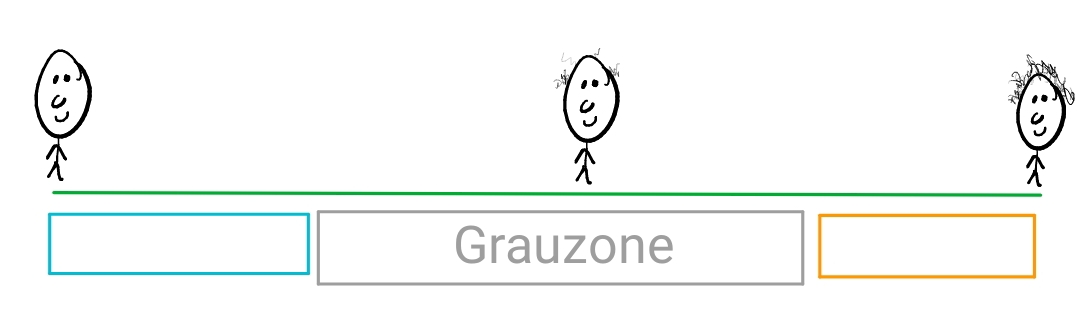
Schon bei diesem Bild fällt uns unmittelbar ein Problem auf: wie steht es um die Grenzen der Grauzone? Gibt es für diese einen klar definierten Cut-Off Punkt? Dies ist das Problem der Vagheit höherer Ordnung: scheinbar ist eine rasiermesserschafte Verortung der Grenzen der Grauzone auch problembehaftet. Wir könnten eine zweite Sorites-Reihe machen, die von links bis irgendwo in die Mitte der Grauzone geht (einem klaren “grauen Fall”) und nun die Frage stellen, wo hört eine Instanz auf klare Glatze zu sein und fängt sie an zur Grauzone zu gehören. Nun hätten wir es mit einer Grauzone2 zu tun in der wir verunsichert sind, während links und rechts der Reihe klare Fälle von Glatzen und Fälle von Grauzonen(1) situiert sind. Solche Nuancen sind nicht Teil des 3-wertigen Bildes.
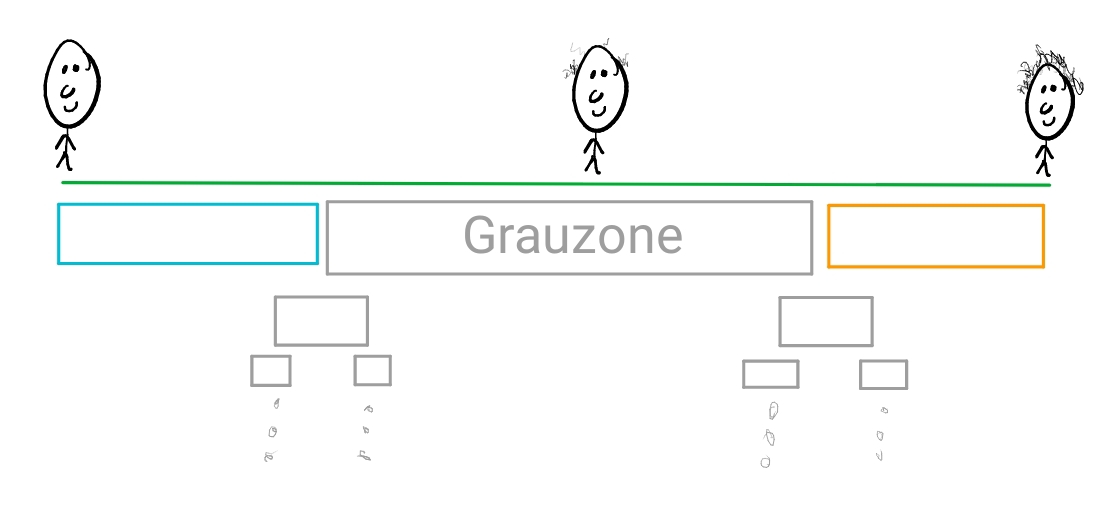
Eine Frage, die sich unmittelbar stellt, ist wie man komplexe Formeln ausgehend von 3-wertigen Belegungen interpretieren soll. Dazu wurden verschiedene Systeme von Wahrheitstabellen vorgestellt. Etwa, könnte man dem Grundgedanken folgen, dass Wahrheitswertlücken “ansteckend” sind in der Hinsicht, dass eine komplexe Formel eine Wahrheitswertlücke aufweist, sobald eine ihrer Komponenten eine Lücke aufweist. Als Ergebnis erhalten wir die Weak Kleene Tabellen:
Für die Konjunktion:
| \(\wedge\) | 0 | u | 1 |
|---|---|---|---|
| 0 | 0 | u | 0 |
| u | u | u | u |
| 1 | 0 | u | 1 |
Für die Disjunktion:
| \(\vee\) | 0 | u | 1 |
|---|---|---|---|
| 0 | 0 | u | 1 |
| u | u | u | u |
| 1 | 1 | u | 1 |
Für die Negation:
| \(\neg\) | |
|---|---|
| 0 | 1 |
| u | u |
| 1 | 0 |
Die Strong Kleene Tabellen folgen dem Prinzip, dass eine wahre Formel eine Disjunktion wahr macht und, dual, eine falsche Formel eine Konjunktion falsch macht. Die Negation bleibt unangetastet:
| \(\wedge\) | 0 | u | 1 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| u | 0 | u | u |
| 1 | 0 | u | 1 |
und
| \(\vee\) | 0 | u | 1 |
|---|---|---|---|
| 0 | 0 | u | 1 |
| u | u | u | 1 |
| 1 | 1 | 1 | 1 |
Wenden wir uns nun der Frage zu, wie dieser Ansatz das Sorites Paradox blockiert. Dazu betrachten wir den Cut-Off Punkt \(i\) am linken Ende der Grauzone.
- der Wert von \(g_i\) ist 1
- der Wert von \(g_{i+1}\) ist \(u\)
- der Wert von \(g_i \rightarrow g_{i+1}\) (hier interpretiert als \(\neg g_i \vee g_{i+1}\) ist damit auch \(u\).
Das heißt, in diesem Ansatz gilt das Toleranzprinzip nicht: manche der Konditionale weisen eine Wahrheitswertlücke auf.
Als weiteren möglichen Kritikpunkt an diesem Ansatz haben wir im Seminar Kit Fines (1997) Kritik an der Wahrheitsfunktionalität diskutiert, sowie Smiths (2009, p. 86) Entgegnung.
Supervaluationismus
Im Supervaluationismus geht man auch von Wahrheitswertlücken aus, allerdings ist der resultierende Ansatz nicht wahrheitswertfunktional. Analog zum Vorgehen in den 3-wertigen Logiken, gehen wir im Sorites Fall von Fällen, die klarerweise wahr, anderen Fällen, die klarerweise falsch, und schließlich Grenzfällen aus. Letztere haben keinen Wahrheitswert. Anstatt einen dritten Pseudowahrheitswert zu benutzen, werden in diesem Kontext meist partielle Belegungen verwendet.
Formal ist eine partielle Belegung eine partielle Funktion von den Atomen der Sprache in \({0,1}\). Die Funktion ist partiell dahingehend, dass sie (möglicherweise) nicht jedem Atom einen Wahrheitswert zuordnet: für manche Atome ist die Funktion nicht definiert. Im Sorites Szenario weist die partielle Belegung \(v\) jeder Aussage \(g_1\), …, \(g_{i}\) den Wert 1 zu (wobei bei \(i+1\) die Grenzfälle beginnen), jeder Aussage \(g_{k+1}\), … \(g_n\) den Wert 0 zu (wobei bei \(k+1\) die Grenzfälle aufhören), und für jede Aussage \(g_{i+1}\), …, \(g_k\) ist die Belegung nicht definiert.
Um die Interpretation komplexer Formeln zu bestimmen, arbeitet man im Supervaluationismus mit sogenannten Precisifications (Präzisierungen) der partiellen Belegung: diese sind klassische (nicht-partielle!) Belegungen \(v’\) für die gilt: für jedes Atom \(p\),
- falls \(v(p) = 1\) dann \(v^{\prime}(p) = 1\)
- falls \(v(p) = 0\) dann \(v^{\prime}(p) = 0\).
Präzisierungen übernehmen alo die Wahrheitswerte der zugrunde liegenden partiellen Belegung und belegen die restlichen Atome klassische mit 1 oder 0.
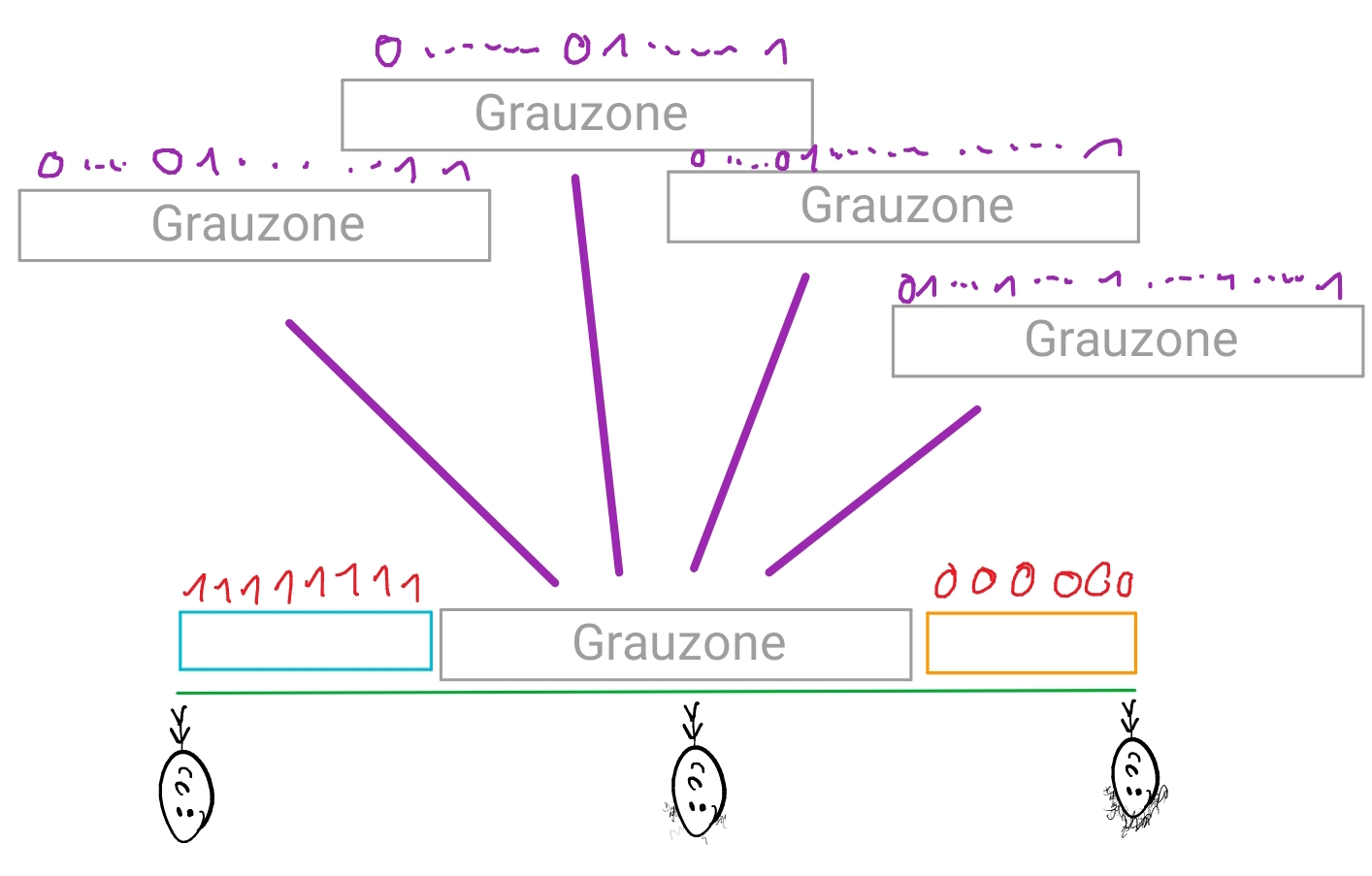
Auf Grundlage dieser Präzisierungen der partiellen Belegung \(v\) ergibt sich dann eine sogenannte Supervaluation \(v^{*}\): eine partielle Interpretation aller Formeln in der gegebenen formalen Sprache (etwa der aussagenlogischen Sprache). Die Definition ist wie folgt, für eine beliebige Formel \(A\):
- \(v^{*}(A) = 1\) gdw für jede Präzisierung \(v^{\prime}\) von \(v\) gilt \(v_M^{\prime}(A) = 1\) (wobei \(M\) das auf \(v^{\prime}\) basierende klassische Modell ist)
- \(v^{*}(A) = 0\) gdw für jede Präzisierung \(v^{\prime}\) von \(v\) gilt \(v_M^{\prime}(A) = 0\)
- \(v^{*}(A)\) ist undefiniert, sonst.
Hier stellt sich die Frage, ob dieses Vorgehen einen Unterschied macht zum Ansatz der 3-wertigen Logik. Ein gravierender Unterschied ist gegeben bezüglich der Wahrheitsfunktionalität.
- Wir gehen davon aus, dass \(g_i\) eine Wahrheitslücke aufweist in unserer partiellen Belegung \(v\). Damit haben auch \(g_i\) und \(\neg g_i\) in \(v^{*}\) keinen Wahrheitswert. Sehen Sie warum? Der Grund ist, dass es klassische Belegungen gibt, die \(g_i\) den Wert 1 zuweisen und damit wird in diesen Modellen \(\neg g_i\) mit 0 interpretiert, es gibt aber auch klassische Belegungen, die \(g_i\) den Wert 0 zuweisen und damit wird in diesen Modellen \(\neg g_i\) mit \(1\) interpretiert. Da sich also unsere Präzisierungen nicht einig sind, erhalten \(g_i\) und \(\neg g_i\) keinen Wahrheitswert in der Supervaluation \(v^{*}\).
- Dennoch gilt, dass \(g_i \vee \neg g_i\) in \(v^{*}\) den Wert 1 hat. Der Grund ist, als klassische Tautologie gilt \(g_i \vee \neg g_i\) in allen Präzisierungen von \(v\).
- Zum Kontrast können wir jedoch beobachten, dass \(g_i \vee g_i\) nicht den Wert 1 in \(v^{*}\) bekommt. Sehen Sie warum?
- Mit der Wahrheitswertfunktionalität würden wir erwarten, dass der Wahrheitswert einer Disjunktion durch die Wahrheitswerte ihrer Komponenten determiniert ist. In diesem Fall haben wir jeweil zwei Fälle, in denen beide Komponenten Wahrheitswertlücken aufweisen, im ersten Fall ist die Disjunktion wahr, im zweiten jedoch falsch!
Im Ansatz des Supervaluationismus wird das Sorites Paradox blockiert durch Aufgabe des Toleranzprinzips. Etwa das erste Konditional \(g_i \rightarrow g_{i+1}\) zu Beginn der Grauzone hat in \(v^{*}\) keinen Wahrheitswert. Der Grund ist, dass manche Präzisierungen \(g_{i+1}\) mit 1 und damit \(g_i \rightarrow g_{i+1}\) mit 1 interpretieren, manche aber \(g_{i+1}\) mit 0 und damit \(g_i \rightarrow g_{i+1}\) mit 0 interpretieren.
In der nächsten Sitzung werden wir nochmal zu einem wahrheitsfunktionalen Ansatz, den der Fuzzy Logiken zurück kommen.
Weiterführende Literatur (im Aufbau)
Zusammenfassungen zum Thema
Kollektionen von Manuskripten
- Kenney, R., & Smith, P. (1996). Vagueness: a reader. : MIT press.
Monographien
- Sorensen, R. (2001). Vagueness and contradiction. Clarendon Press.
- Williamson, T. (2002). Vagueness. Routledge.
- Shapiro, S. (2006). Vagueness in context. Oxford University Press.
- Smith, N. J. J. (2008). Vagueness and degrees of truth. Oxford University Press.
Andere erwähnte Werke
Im Kontext des Epistemizismus
- Sorensen, R. (2001). Vagueness and contradiction. Clarendon Press.
- Williamson, T. (2002). Vagueness. Routledge.
Im Kontext der 3-wertigen Logiken
- Kleene, S. (1952). Introduction to metamathematics. Amsterdam: Van Nostrand.
- Fine, K. (1975). Vagueness, truth and logic. Synthese, 30(3-4), 265–300. (Kritik)
Vagheit höhere Ordnung
- Varzi, A. C. (2003). Higher-order vagueness and the vagueness of “vague”. Mind, 112(446), 295–298.
Im Kontext des Margin of Error und des Gettier Problems
- Gettier, E. (1963). Is Justified True Belief Knowledge? Analysis, 23(6), 121–123.
- Dretske, F. (1971). Conclusive Reasons. Perception, Knowledge, and Belief, 3–29.
- Nozick, R. (1981). Philosophical explanations. : Harvard University Press.
- Kripke, S. A. (2011). Nozick on knowledge*. Philosophical Troubles. Collected Papers, Volume 1, 161–224.
Im Kontext des Supervaluationismus
- Van Fraassen, B. C. (1966). Singular terms, truth-value gaps, and free logic. The journal of Philosophy, 63(17), 481–495.
- Fine, K. (1975). Vagueness, truth and logic. Synthese, 30(3-4), 265–300.
- Varzi, A. C. (2007). Supervaluationism and its logics. Mind, 116(463), 633–676.
-
Gewöhnlich werden Sorites Reihen bzgl. unserer visuellen Wahrnehmung formuliert, auch andere Sinne können jedoch betroffen sein. Vgl. hierzu etwa We Made a Tool So You Can Hear Both Yanny and Laurel - The New York Times. ↩︎
-
Shapiro geht hier von einem vagen Prädikat \(P\) aus (etwa: “… hat eine Glatze”). Im Zitat darunter geht Smith von einem vagen Prädikat \(F\) aus. ↩︎
-
Smith hält dieses Argument als nicht ausreichend und diskutiert den Fall eine ausreichend ähnlichen kontrafaktischen Situation, in der der Sprachgebrauch einen minimal unterschiedlichen Cut-Off Punkt festgelegt hat. Die Situtation ist für \(S\) ausreichend ähnlich, da sie nicht in der Lage wäre, die feinen Nuancen des unterschiedlichen Sprachgebrauchs zu realisieren. ↩︎