Session 2: The limitations of Standard Deontic Logic
In Standard Deontic Logic (henceforth, SDL), the following is a valid principle:
- If \(\vdash A \rightarrow B\) then also \(\vdash \mathsf{O} A \rightarrow \mathsf{O} B\).
This principle is sometimes called modal inheritance (for the \(\mathsf{O}\) operator). We will abbreviate it with O-Inh. It means, if \(A\) logically implies \(B\) then also \(\mathsf{O}A\) implies \(\mathsf{O} B\).
Several problems with this principle have been pointed out in the literature, some of which are considered as core problems of SDL. Consider the following obligation:
- It ought to be that Peter, who has been robbed, is helped. (S1)
Now, if we interpret this in the following way
- It ought to be that (Peter who has been robbed is helped). (SWC1)
we face the problem that from
- “Peter who has been robbed is helped”
follows
- “Peter has been robbed.”
So with O-Inh we get:
- It ought to be that (Peter has been robbed).
This is clearly not intuitive.
Forrester (1984) points out that in such cases we also have also the option to interpret S1 differently:
- Peter has been robbed. It ought to be that Peter is helped. (SNS1)
The difference between SWC1 and SNS1 is a matter of scope: in SWC1 the scope of the \(\mathsf{O}\)-operator (i.e., the part of the sentence to which it applies) is the full statement “Peter who has been robbed is helped” while in SNS1 it is restricted to “Peter is helped”. In the first case the scope is wide, in the second narrow.
Cases like our example have been dubbed Good Samaritan in the literature. 1
Aqvist (1967) proposed an epistemic version of it:
- It ought to be that Smith refrains from robbing Jones.
- I ought to know that Smith robs Jones. 2
Following what most epistemologists tell us about the nature of knowledge, from knowing that \(A\) follows that \(A\). Formally,
- \(\vdash \mathsf{K}A \rightarrow A\). Here \(\mathsf{K}\) is a modal operator that expresses knowledge (of a given agent) in its argument.
Now, if we plug in O-Inh we get from 2 (formalized as \(\mathsf{O} \mathsf{K} p\)):
- It ought to be that Smith robs Jones. (Formally, \(\mathsf{O} p\).) 3
In this example a solution such as above with simply changes the scope of \(\mathsf{O}\), seems to not be available since it essentially concerns the interaction of the deontic modality \(\mathsf{O}\) with the epistemic modality \(\mathsf{K}\).
Forrester in his article investigates whether there are cases where (a) the scoping solution does not work and (b) that are not related to the nesting of (different types of) modalities (like Aqvist’s case). For this, he proposes the following example:
- In general you ought not to kill.
- However, if you kill, you better do so in a gentle way.
The second obligation is a so-called contrary-to-duty obligation. Such obligations help us to express obligations that are triggered in case other, more general, obligations are violated. In many scenarios it seems reasonable to differentiate between ideal, sub-ideal and bad situations. E.g., best if no killing happens, worse is if a killing happens, but if so it is better if the killing is at least gently. We differentiate often between better and worse ways of violating obligations when we assign blame, responsibility, or punishment to agents. The punishment and blame for a violent killing may be in many situations less severe than for a gentle killing, to utilize Forrester’s morbid example a bit more.
Given this motivation or justification of contrary-to-duty norms, we should consider the example above consistent. Especially, a deontic logic when applied to it should not render it inconsistent. Let us therefore check what happens when we formalize the example in SDL. I first show a proof tree and then comment on the various steps:

In blue we introduce different types of fact which characterize this example.
- Two facts are independent from deontic information: first, the killing takes place (\(k\)), second, killing gently implies killing (\(\vdash g \rightarrow k\)). We write this as a logical axiom since we consider this a conceptual truth which should hold in every possible world.
- We have two norms:
- The categorical obligation not to kill (\(\mathsf{O} \neg k\)).
- The conditional obligation that if you kill you ought to kill gently (\(\mathsf{O}(k \rightarrow g)\)).
FDet (in red) is a principle that expresses that conditional obligations should be “detachable”: if the condition of the obligation is true, the obligation applies. In our example, if you really do kill, you have to do it gently (\(k \rightarrow \mathsf{O}g\)). This is not a general principle of SDL, but rather stipulated by Forrester.
So, applying Modus Ponens (MP) to the fact \(k\) and \(k \rightarrow \mathsf{O}g\) we obtain \(\mathsf{O}g\) (in orange).
O-Inh was discussed above and is used in our example to derive \(\mathsf{O}g \rightarrow \mathsf{O} k\) (in purple).
Now, in SDL we have the principle O-Cons expressing that there are no deontic conflicts, that is, situation where \(\mathsf{O}A\) and \(\mathsf{O}\neg A\) holds for some formula \(A\). So, if \(\mathsf{O}\neg k\) holds, \(\mathsf{O}k\) cannot also hold and therefore \(\neg \mathsf{O}k\) holds (in light blue). If you want to see how this plays out in the semantics of SDL, we’ll address this in a second.
From \(\mathsf{O}g\) and \(\mathsf{O}g \rightarrow \mathsf{O}k\) we can, via Modus Ponens, derive \(\mathsf{O}k\) (in a box, because this is really bad! – if you don’t see why immediately, shortly think about it …).
Now, classical logic gives us an additional problem, namely that from a contradiction, like having \(\mathsf{O}k\) and \(\neg \mathsf{O}k\), anything follows. We write \(\bot\) for the falsity symbol, which is always interpreted as false, as the name suggests.
So why is this really bad? It means SDL renders a scenario as inconsistent that is intuitively speaking perfectly reasonable. And even if you would block the last inference (logical explosion) by choosing, for instance, a paraconsistent logic, we’d still be left with \(\mathsf{O}k\) which seems not a reasonable inference to make in the given context (or ever?).
Again, the culprit seems to be O-Inh: it seems not reasonable to infer from \(\mathsf{O}g\) the obligation to kill. As you can see, now we have no way out by simply scoping our \(\mathsf{O}\) in a different way, as in the example in the beginning of this entry. Similarly, the solution cannot lie with changing the way \(\mathsf{O}\) interacts with the epistemic modality \(\mathsf{K}\) as in Aqvist’s example. How will we get out of this misery! Stay tuned … for future sessions.
Let us in the end shortly see why the principles used in Forrester’s proof are indeed valid in SDL.
We first consider O-Inh. Suppose \(\vdash g \rightarrow k\) and so \(g \rightarrow k\) holds in every model at every world. We want to show that then also \(\mathsf{O}g \rightarrow \mathsf{O}k\) holds in every model at every world. So let \(M = \langle W, R, @, v \rangle\) be an arbitrary SDL-model and \(w \in W\) be an arbitrary world. We want to show that \(M,w \models \mathsf{O}g \rightarrow \mathsf{O}k\). We show that if \(M,w \models \mathsf{O}g\) then \(M,w \models \mathsf{O}k\). (Check the truth-table for \(\rightarrow\) to see why this is sufficient.)
- Suppose \(M,w \models \mathsf{O}g\).
- Thus, for all \(w^{\prime} \in W\) for which \(w R w^{\prime}\), \(M,w^{\prime} \models g\).
- Since \(g \rightarrow k\) is a logical axiom, it holds in every world.
- In particular, for all \(w^{\prime} \in W\) for which \(w R w^{\prime}\), \(M, w^{\prime} \models g \rightarrow k\).
- Since our worlds obey the rules of classical logic, in particular Modus Ponens is valid in them. So, for all \(w^{\prime} \in W\) for which \(w R w^{\prime}\), \(M, w^{\prime} \models k\).
- Thus, \(M,w \models \mathsf{O}k\).
It is an exercise to show that the principle O-Cons holds in all SDL-models.
Exercise: The Andersonian Reduction
Anderson proposed to utilize a violation constant \(\mathbf{v}\) to express or define an obligation operator:4
- \(\mathsf{O} A\) is defined by \(\neg A \Rightarrow \mathbf{v}\): \(A\) is obliged if \(\neg A\) leads to violation.
We have not given a precise meaning to \(\Rightarrow\) yet. Anderson had in mind an implication from the family of relevance logics. In the literature it has often been proposed to use strict implication instead (also since it has a comparably simple logical model):
- \(\mathsf{O} A\) is defined by \(\Box(\neg A \rightarrow \mathbf{v})\): \(A\) is obliged if \(\neg A\) necessarily leads to violation.
Permission can then be defined by:
- \(\mathsf{P}A\) is defined by \(\Diamond(A \wedge \neg \mathbf{v})\): \(A\) is permissible if it is possible that \(A\) and at the same time no violation takes place.
The necessity modality \(\Box\) may be the modality from the modal logic K or T. In both logics, just like in SDL, a model is a quadruple \(M = \langle W, R, @, v \rangle\) with a non-empty set of worlds \(W\), an accessibility relation \(R\) among worlds, an actual world \(@ \in W\) and an interpretation of atoms at worlds \(v\). For K there are no restrictions on \(R\), while for T, \(R\) is reflexive, i.e., for all worlds \(w \in W\), \(wRw\). We have one special requirement for \(\mathbf{v}\) that every model and every world has to fulfill: there is always an accessible world without violation.
- For all \(w \in W\) there is a \(w^{\prime} \in W\) for which \(wRw^{\prime}\) and \(M,w^{\prime} \models \neg \mathbf{v}\).
Note that this requirement implies that the accessibility relation will be serial, just like in SDL.
Formulas at worlds are interpreted just as in SDL, where
- \(M,w \models \Box A\) (“it is necessary that \(A\)") iff for all \(w^{\prime}\) for which \(wRw^{\prime}\), \(M,w^{\prime} \models A\).
- \(M,w \models \Diamond A\) (“it is possibly that \(A\)") iff there is an \(w^{\prime}\) for which \(w R w^{\prime}\) and \(M,w^{\prime} \models A\).
Try to verify that the following principles of SDL are also valid in Anderson’s systems based on K and T (at every world in every model):
- \(\mathsf{O}p \rightarrow \mathsf{P} p\)
- \((\mathsf{O}p \wedge \mathsf{O}q) \rightarrow \mathsf{O}(p \wedge q)\)
Show that additionally we get:
- \(\Box p \rightarrow \mathsf{O}p\)
- \(\Box(p \rightarrow q) \rightarrow (\mathsf{O}p \rightarrow \mathsf{O} q)\) (Note the similarly to O-Inh.)
- and where \(R\) is reflexive: \(\mathsf{O}(\mathsf{O}p \rightarrow p)\).
Extra question: in your opinion, in what sense (if any) does Anderson’s system give a “reduction” of deontic logic to alethic modal logic, and in what sense (if any) not?
Solutions to the exercises from last time
Exercise 1
We have the following model \(M = (W, R, @, v)\) where
- \(W = \{@, w\}\)
- \(R = \{(@,w), (w,w)\}\)
and \(v\) is given by (to keep things simple we work with a language with only two atoms \(p,q\)):
| \(@\) | \(w\) | |
|---|---|---|
| \(p\) | 1 | 1 |
| \(q\) | 0 | 0 |
Which of the following statements is true:
- \(M,@ \models \mathsf{O}p\)
- \(M,@ \models \mathsf{O} \mathsf{O}p\)
- \(M,@ \models \mathsf{P} q\)
- \(M,@ \models \mathsf{O}p \rightarrow q\).
- \(M,@ \models \mathsf{O}p \rightarrow p\).
Solution
| Item | Yes/No |
|---|---|
| 1. | Yes |
| 2. | Yes |
| 3. | No |
| 4. | Yes |
| 5. | Yes |
Exercise 2
Can you find a model with only two worlds and a serial accessibility relation for which it doesn’t hold that \(M,@ \models \mathsf{O} \mathsf{O} p \rightarrow \mathsf{O}p\)?
Solution
Take
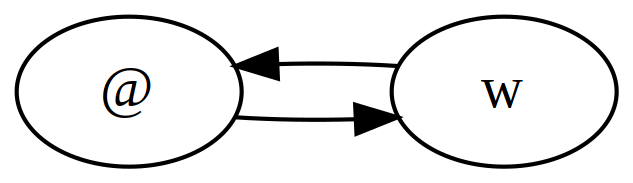
where
| world | p |
|---|---|
| @ | 1 |
| w | 0 |
In this case we have:
- \(M,@ \models \mathsf{O} \mathsf{O} p\) but
- \(M,@ \models \neg \mathsf{O}p\).
Exercise 3
How many worlds does a model with serial accessibility relation have, whose accessibility relation is transitive and irreflexive. Recall:
- transitive means that for all \(w_1, w_2, w_3\) we have that if \(w_1 R w_2\) and \(w_2 R w_3\) then \(w_1 R w_3\).
- irreflexive means that for all \(w\) we don’t have \(wRw\).
Solution
There is no model with a finite set of worlds that fulfills our requirements. Assume for a contradiction there is such a model \(M= \langle W, R, @, v \rangle\) where \(W = \{ @, w_1, \dotsc, w_n\}\) for some natural number \(n\).
- Since \(R\) is serial and irreflexive, there must be a \(w \neq @\) in \(W\) such that \(@Rw\). Without loss of generality assume that \(w = w_1\).
- For the same reason there must be a \(w \neq w_1\) such that \(w_1Rw\). It cannot be that \(w = @\) since otherwise by transitivity \(w_1Rw_1\). So, \(w \in W \setminus \{@,w_1\}\). Without loss of generality assume that \(w = w_2\).
- Again, following the same line of reasoning there must be a \(w \neq w_2\) such that \(w_2Rw\). It cannot be that \(w \in \{@,w_1\}\) since otherwise by transitivity \(w_2Rw_2\). So \(w \in W \setminus \{@,w_1,w_2\}\). Without loss of generality assume that \(w =w_3\).
- etc.
- Following the same line of reasoning there must be a \(w \neq w_n\) such that \(w_nRw\). It cannot be that \(w \in \{@,w_1, \ldots, w_{n-1}\}\) since otherwise by transitivity \(w_n R w_n\). So \(w \in W\) which is a contradiction.
Exercise 4
Construct a model \(M = (W, R, @, v)\) in which the following are true:
- \(M,@ \models \mathsf{O}(p \vee q)\)
- \(M,@ \models \neg\mathsf{O}p \wedge \neg \mathsf{O}q\)
- \(M,@ \models \mathsf{P}p\)
- \(M,@ \models \mathsf{P}q\)
Solution
Let the model be given by
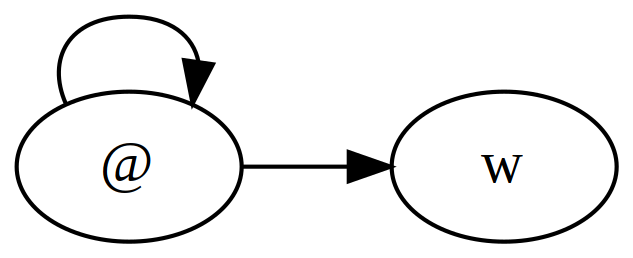
where
| world | p | q |
|---|---|---|
| @ | 1 | 0 |
| w | 0 | 1 |
References
- Anderson, A. R. (1958). A reduction of deontic logic to alethic modal logic. Mind, 67(265), 100–103.
- Aqvist, L. (1967). Good samaritans, contrary-to-duty imperatives, and epistemic obligations. Nous, 1(4), 361–379.
- Chisholm, R. M. (1963). Contrary-to-duty imperatives and deontic logic. Analysis, 24(), 33–36.
- Forrester, J. . (1984). Gentle murder, or the adverbial samaritan. Journal of Philosophy, 81, 193–197.
- Kanger, S. (1971). New foundations for ethical theory. In R. Hilpinen (Eds.), Deontic Logic: Introductory and Systematic Readings (pp. 36–58). D. Reidel Company, Dordrecht.
-
Aqvist doesn’t give us much of context as to why I ought to know that. All that matters to him is that the two obligations are intuitively speaking consistent. ↩︎
-
If you are complaining that we happily jump from ought-to-be to ought-to-do and back, you are right. I am following Aqvist here: one could be more hygienic and transform the second obligation into an ought-to-be: It ought to be that I know that … ↩︎
-
A dual approach, not with a violation constant, but with an ideality constant, has been proposed by Stig Kanger in New foundations for ethical theory. In R. Hilpinen (Eds.), Deontic Logic: Introductory and Systematic Readings (pp. 36–58). D. Reidel Company, Dordrecht. Anderson’s approach can be found in A reduction of deontic logic to alethic modal logic. Mind, 67(265), 100–103, 1958. ↩︎