Session 5: More on SDDL and Solution to Exercises

In the last session we had the following exercises.

Exercise 1

How does an SDDL-model of the Chisholm scenario look like? Recall, the Chisholm scenario consists of the following norms:

1. $\mathsf{O}(g \mid \top)$
2. $\mathsf{O}(t \mid g)$
3. $\mathsf{O}(\neg t \mid \neg g)$

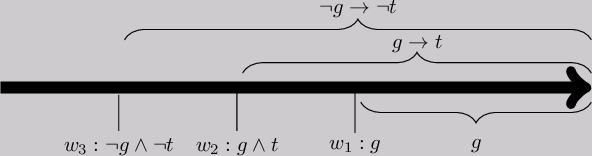
Using the semantics clauses for the $\mathsf{O}$-operator, we know that in any model of our given norms, there have to be three worlds that serve as cutoff points:

• $w_1$ for which $M,w_1 \models g \wedge \top$ (which means: $M,w_1 \models g$) and for all $w \ge w_1$, $M,w \models \top \rightarrow g$ (which means: $M,w \models g$);
• $w_2$ for which $M,w_2 \models g \wedge t$ and for all $w \ge w_2$, $M,w \models g \rightarrow t$;
• $w_3$ for which $M,w_3 \models \neg g \wedge \neg t$ and for all $w \ge w_3$, $M,w_3 \models \neg g \rightarrow \neg t$.

A model of the Chisholm scenario may look, for instance, as follows:

Exercise 2

Do the following principles hold in SDDL (that is: are they validated in each SDDL model at each world)?

1. $(\mathsf{O}(p \mid q) \wedge \mathsf{O}(s \mid q)) \rightarrow \mathsf{O}(p \wedge s \mid q)$
2. $\mathsf{O}(p \mid q) \rightarrow \mathsf{O}(p \mid q \wedge s)$
3. $\mathsf{O}(p \mid q) \rightarrow \mathsf{O}(p \wedge s \mid q)$
4. $\mathsf{O}(p \mid q) \rightarrow \mathsf{O}(p \wedge q \mid q)$
5. $\mathsf{O}(p \mid q) \wedge \mathsf{O}(p \mid s) \rightarrow \mathsf{O}(p \mid q \wedge s)$
6. $\mathsf{O}(p \mid q) \rightarrow \mathsf{P}(p \mid q)$
7. $\mathsf{O}(p \mid q) \rightarrow \mathsf{O}(q \rightarrow p \mid \top)$
8. $\mathsf{O}(p \rightarrow q \mid s) \rightarrow (\mathsf{O}(p \mid s) \rightarrow \mathsf{O}(q \mid s))$
9. $(\mathsf{O}(p \mid q) \wedge \mathsf{O}(s \mid q)) \rightarrow \mathsf{O}(p \mid q \wedge s)$

Ad 1

I have demonstrated a proof of property 1 in details in the last blog entry.

Ad 2

I have given a counter-example in the last blog entry.

Ad 3

This property doesn’t hold. Here is a counter-example.

Our model $M = \langle \{w\}, \{(w,w)\}, v \rangle$ has exactly one world for which

world	$p$	$q$	$s$
$w$	1	1	0

Note that $M \models \mathsf{O}(p \mid q)$ while it is not the case that $M \models \mathsf{O}(p \wedge s \mid q)$ since there is no potential cutoff point, i.e., there is no world where $p \wedge s \wedge q$ is true.

Ad 4

This holds. Suppose we have a model $M = \langle W, \ge, v \rangle$ where $M \models \mathsf{O}(p \mid q)$. Thus, there is a $w_1 \in W$ for which

1. $M,w_1 \models p \wedge q$ and
2. for all $w \ge w_1$, $M,w \models q \rightarrow p$.

Since for all worlds $w$, $M,w \models q \rightarrow q$ we get with item 2,

$3$. $M,w \models q \rightarrow (p \wedge q)$ for all worlds $w \ge w_1$.

So, with items 1 and 3, $M \models \mathsf{O}(p \wedge q \mid q)$.

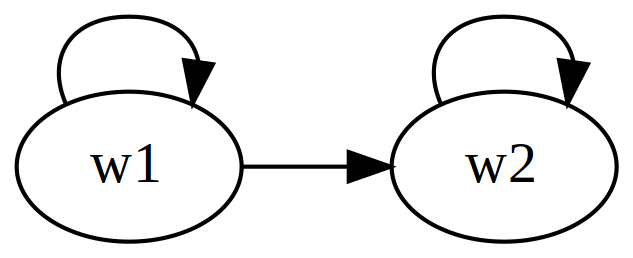
Ad 5

This does not hold in general. We give a counter-example, i.e., a model $M = \langle W, \ge, v \rangle$ for which (i) $M \models \mathsf{O}(p \mid q) \wedge \mathsf{O}(p \mid s)$ while (ii) it is not the case that $M \models \mathsf{O}(p \mid q \wedge s)$.

Let $W = \{w_1, w_2\}$ where the assignment is as follows:

world	$p$	$q$	$s$
$w_1$	1	1	0
$w_2$	1	0	1

Let ${\ge} = \{(w_1,w_1), (w_2,w_2), (w_2,w_1)\}$. It is easy to see that $M$ fulfills our desiderata.

Ad 6

This holds in SDDL. Recall that $\mathsf{P}(p \mid q)$ is defined by $\neg \mathsf{O}(\neg p \mid q)$. Suppose we have an arbitrary model $M = \langle W, \ge, v \rangle$ in which $\mathsf{O}(p \mid q)$ holds. (If it doesn’t then obviously $M \models \mathsf{O}(p \mid q) \rightarrow \mathsf{P}(p \mid q)$.) Thus, there is a $w_1 \in W$ for which $M \models p \wedge q$ and for all $w \ge w_1$, $M,w \models q \rightarrow p$.

We have to show that $M \models \neg \mathsf{O}(\neg p \mid q)$. That means, for every potential cutoff world $w_2$, i.e., every world $w_2$ for which $M,w_2 \models q \wedge \neg p$, there must be a world $w_2^{\prime} \ge w_2$ for which $M,w_2^{\prime} \models \neg (q \rightarrow \neg p)$ (and hence, $M,w_2^{\prime} \models q \wedge p$).

• If there is no potential cutoff point $w_2$, then clearly $M \models \neg \mathsf{O}(\neg p \mid q)$.
• Else, let $w_2$ be such a world for which $M,w_2 \models q \wedge \neg p$. Note that $w_1 \ge w_2$, since for all $w \ge w_1$, $M,w \models \neg ( q \wedge \neg p)$ (since $M,w \models q \rightarrow p$). Also recall that $M,w_1 \models \neg(q \rightarrow \neg p)$.

This concludes our proof.

Ad 7

This holds. To show this we again assume an arbitrary model $M = \langle W, \ge, v \rangle$ for which $M \models \mathsf{O}(p \mid q)$.

Thus, there is a $w_1 \in W$ for which $M,w_1 \models p \wedge q$ and for all $w \ge w_1$, $M,w \models q \rightarrow p$. Clearly, $M,w_1 \models \top \wedge (q \rightarrow p)$ and for all $w \ge w_1$, $M,w \models \top \rightarrow (q \rightarrow p)$. Thus, $M \models \mathsf{O}(q \rightarrow p \mid \top)$.

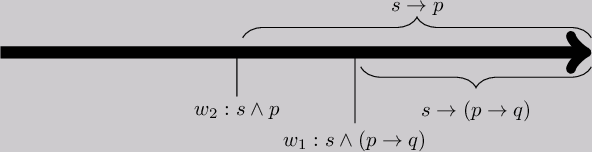
Ad 8

This holds. Let $M = \langle W, \ge, v \rangle$ be a model for which $M \models \mathsf{O}(p \rightarrow q \mid s)$. Thus, there is a $w_1 \in W$ for which $M,w_1 \models s \wedge (p \rightarrow q)$ and for all $w \ge w_1$, $M,w \models s \rightarrow (p \rightarrow q)$.

Now if it isn’t the case that $M \models \mathsf{O}(p \mid s)$ then $M \models \neg \mathsf{O}(p \mid s)$ and therefore $M \models \mathsf{O}(p \mid s) \rightarrow \mathsf{O}(q\mid s)$. Thus, $M \models \mathsf{O}(p \rightarrow q \mid s) \rightarrow (\mathsf{O}(p \mid s) \rightarrow \mathsf{O}(q \mid s))$.

Suppose now that $M \models \mathsf{O}(p \mid s)$. Thus, there is a $w_2 \in W$, for which $M,w_2 \models s \wedge p$ and for all $w \ge w_2$, $M,w \models s \rightarrow p$. We need to show that $M \models \mathsf{O}(q\mid s)$.

We have two possible scenarios. Either $w_1 \ge w_2$

or $w_2 \ge w_1$:

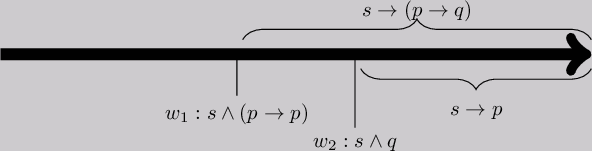
We discuss the former case. (The latter case is similar.) In order to show that $M \models \mathsf{O}(q \mid s)$ we need to locate a world $w_3$ for which $M,w_3 \models q \wedge s$ and for all $w \ge w_3$ ,$M,w \models s \rightarrow q$. Let for this $w_3 = w_1$. Note that $M,w_1 \models s \wedge (p \rightarrow q)$ and since $w_1 \ge w_2$, $M,w_1 \models s \rightarrow p$. Thus, $M,w_1 \models s \rightarrow q$ (by classical propositional logic) and since $M,w_1 \models s$ also $M,w_1 \models q$ (by Modus Ponens). Altogether, $M,w_1 \models s \wedge q$. Now, since for all $w \ge w_1$ we have both $M,w \models s \rightarrow p$ and $M,w \models s \rightarrow (p \rightarrow q)$ we also have $M,w \models s \rightarrow q$.

Ad 9

This principle holds. To prove it we consider a model $M = \langle W, \ge, v \rangle$ for which $M \models \mathsf{O}(p \mid q) \wedge \mathsf{O}(s \mid q)$ and show that $M \models \mathsf{O}(p \mid q \wedge s)$.

• Since $M \models \mathsf{O}(p \mid q)$ there is a $w_1 \in W$ for which $M,w_1 \models p \wedge q$ and for all $w \ge w_1$, $M,w \models q \rightarrow p$.
• Since $M \models \mathsf{O}(s \mid q)$ there is a $w_2 \in W$ for which $M, w_2 \models q \wedge s$ and for all $w \ge w_2$, $M,w \models q \rightarrow s$.

We have two possible scenarios: $w_1 \ge w_2$ and $w_2 \ge w_1$. We discuss the former (the latter is analogous).

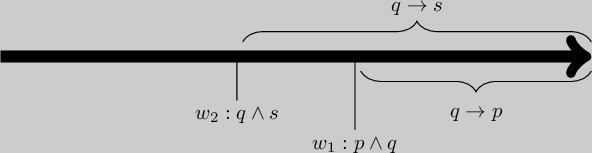
In order to verify that $M \models \mathsf{O}(p \mid q \wedge s)$ we need to find a world $w_3$ for which $M,w_3 \models p \wedge q \wedge s$ and for all $w \ge w_3$, $M,w \models (q \wedge s) \rightarrow p$. Let $w_3 = w_1$. Then $M,w_3 \models p \wedge q \wedge s$ since $M,w_1 \models p \wedge q$ and since $w_1 \ge w_2$, $M,w_1 \models q \rightarrow s$ and so by Modus Ponens also $M,w_1 \models s$. Furthermore, for all $w \ge w_3$, $M,w \models (q \wedge s) \rightarrow p$ since $M,w \models q \rightarrow p$ and $M,w \models q \rightarrow s$.

Some Potential Problems with SDDL

We spent the last minutes of our session discussion two potential problems with SDDL.

The problem with Rational Monotony

One is that from $\mathsf{O}(\neg f \mid \top)$ and $\mathsf{P}(a \mid \top)$ follows in SDDL $\mathsf{O}(\neg f \mid a)$. In other words, the following is validated in SDDL: $(\mathsf{O}(\neg f \mid \top) \wedge \mathsf{P}(a \mid \top) ) \rightarrow \mathsf{O}(\neg f \mid a)$.

This is problematic for specificity-like scenarios such as Horty’s asparagus. After all, the following setting seems perfectly consistent:

1. In general, you ought not to eat with your fingers. $\mathsf{O}(\neg f \mid \top)$
2. However, if you’re being served asparagus, you are allowed to eat with your fingers. $\mathsf{P}(f \mid a)$.

Note that item 2 is equivalent to $\neg \mathsf{O}(\neg f \mid a)$. So, if we, additionally to our norms 1 and 2, have also $\mathsf{P}(a \mid \top)$ (“In general you’re allowed to eat asparagus."), we get an inconsistent set of norms from which anything follows. This seems not satisfactory.

Since in classical propositional logic we have $(A \wedge B) \rightarrow C$ is equivalent to $(A \wedge \neg C) \rightarrow \neg B$ we can transform the principle above to: $(\mathsf{O}(\neg f \mid \top) \wedge P(f \mid a)) \rightarrow \mathsf{O}(\neg a \mid \top)$. This seems similarly counter-intuitive.

The deeper reason behind these kind of problems is that Rational Monotony is a principle underlying SDDL:

• Rational Monotony: From $\mathsf{O}(A \mid B)$ and $\mathsf{P}(C \mid B)$ follows $\mathsf{O}(A \mid B \wedge C)$.

Exercise: Try to show that Rational Monotony holds in SDDL.

The problem with factual detachment

In SDDL, as we presented it, we have no way of validating Factual Detachment, the principle which says that if $A$ and $\mathsf{O}(B \mid A)$ then $\mathsf{O}B$.

Clearly, we would like to derive from conditional obligations and the given fact, the actual unconditional obligations that guide the actions of an agent. This is in general tricky, since we need to take into account exceptions and contrary-to-duty obligations. E.g., in the asparagus example, if we’re served asparagus the more general obligation to not eat with your fingers should be blocked.

One possible way to equip SDDL with factual detachment is by making use of an actual world. Then models are quadruples $M = \langle W, \ge, v, @ \rangle$ where $@ \in W$ is the “actual world”. We define $M \models A$ iff $M,@ \models A$. Now, suppose we have the premise set $\{p, \mathsf{O}(q \mid p)\}$. A model may look as follows:

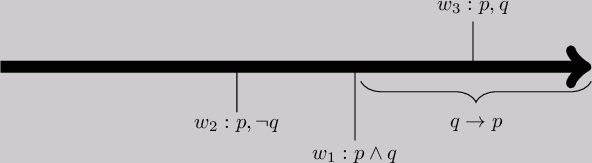
Now, if our actual world $@$ is at least as ideal as $w_1$, we have $M,@ \models q$. However, if we are in a less ideal world than $w_1$ we might have to deal with a world for which $M,@ \models \neg q$. So,

• Problem 1: How to situate the actual world in the “right spot”? The right spot seems to be as ideal as the given premises allow for.

Another problem is that even if $@ = w_3$, we get $M,@ \models q$ while we expect $M,@ \models \mathsf{O}q$. Indeed we don’t want to derive new facts but rather unconditional obligations.

• Problem 2: How to model unconditional obligations in SDDL?

The problem of factual detachment will still concern us some more in future sessions.