Exercises for Session 6 (Supererogation)

In the last session Laura and Thomas presented McNamara’s account of supererogation, as presented in his 1996 article in Mind. In order to get a better grip on his semantic framework, we investigate some properties that may hold or may not hold in his system. Consider always first what your pre-analytic intuitions tell you about the property and decide for yourself whether the formal framework is useful to get a more precise understanding of the underlying concepts.

We first recall some basic definitions. A model in McNamara’s system is given by \(M = \langle W, \ge, v\rangle\) where \(W\) is a non-empty set of worlds, \(\ge\) is a reflexive, transitive, and connected ordering on \(W\), and \(v\) is an assignment of truth-values to atoms \(v\) in each world.¹ Think of it as follows: we’re situated at in an actual situation (McNamara refers to it as the “homey” world) and the worlds in \(W\) are all accessible worlds from homey, all of which are acceptable relative to our moral standards. This is basically the picture from SDL. We didn’t yet talk about the ordering \(\ge\), but this already allows us to define several deontic notions analogously to SDL:²

Task 1: look up the informal meaning of the operators and then fill in the white box. Try the latter without looking up how McNamara defines it. This will be a good test whether your intuitions fall in the right place and whether you find McNamara’s account natural.


\(M \models \mathsf{OB} A\)	iff	\(\fbox{~~~~~~~~~~~~~~~~~~~~~ ? ~~~~~~~~~~~~~~~~~~~}\).
\(M \models \mathsf{PE} A\)	iff	\(\fbox{~~~~~~~~~~~~~~~~~~~~~ ? ~~~~~~~~~~~~~~~~~~~}\).
\(M \models \mathsf{IM} A\)	iff	\({\fbox{~~~~~~~~~~~~~~~~~~~~~ ? ~~~~~~~~~~~~~~~~~~~}}\).
\(M \models \mathsf{GR} A\)	iff	\({\fbox{~~~~~~~~~~~~~~~~~~~~~ ? ~~~~~~~~~~~~~~~~~~~}}\).
\(M \models \mathsf{OP} A\)	iff	\({\fbox{~~~~~~~~~~~~~~~~~~~~~ ? ~~~~~~~~~~~~~~~~~~~}}\)


\(M \models \mathsf{OB} A\)	iff	\(M,w \models A\) for all \(w \in W\).
\(M \models \mathsf{PE} A\)	iff	\(M,w \models A\) for some \(w \in W\).
\(M \models \mathsf{IM} A\)	iff	\(M,w \not \models A\) for all \(w \in W\).
\(M \models \mathsf{GR} A\)	iff	\(M,w \not \models A\) for some \(w \in W\).
\(M \models \mathsf{OP} A\)	iff	\(M,w \models A\) and \(M,w’ \models A\) for some \(w,w’ \in W\)

The difference to SDL is that, similar to SDDL, we now impose an ideality or betterness ordering among the worlds: \(w \ge w^{\prime}\) expresses that \(w\) is at least as good as \(w^{\prime}\). This additional ingredient allows us to express more subtle differences that are needed for a notion of supererogation. (Recall, how a similar move helped us to deal with Contrary-to-Duty obligations in the context of SDDL.)

Task 2: again, look up the informal meaning of the operators and then fill in the white box. Try the latter without looking up how McNamara defines it. This will be a good test whether your intuitions fall in the right place and whether you find McNamara’s account natural.


\(M \models \mathsf{MI} A\)	iff	\({\fbox{~~~~~~~~~~~~~~~~~~~~~ ? ~~~~~~~~~~~~~~~~~~~}}\).
\(M \models \mathsf{MA} A\)	iff	\({\fbox{~~~~~~~~~~~~~~~~~~~~~ ? ~~~~~~~~~~~~~~~~~~~}}\).
\(M \models \mathsf{SI} A\)	iff	\({\fbox{~~~~~~~~~~~~~~~~~~~~~ ? ~~~~~~~~~~~~~~~~~~~}}\).
\(M \models \mathsf{SU} A\)	iff	\({\fbox{~~~~~~~~~~~~~~~~~~~~~ ? ~~~~~~~~~~~~~~~~~~~}}\).
\(M \models \mathsf{IN} A\)	iff	\({\fbox{~~~~~~~~~~~~~~~~~~~~~ ? ~~~~~~~~~~~~~~~~~~~}}\)


\(M \models \mathsf{MI} A\)	iff	\(M,w \models A\) for all \(w \in \min(W)\).
\(M \models \mathsf{MA} A\)	iff	\(M,w \models A\) for all \(w \in \max(W)\).
\(M \models \mathsf{SI} A\)	iff	There are \(B \in \{ A, \neg A\}\) and \(w \in W\) such that for all \(w’\) for which \(w \le w’\) and \(w’ \le w\) we have \(M,w’ \models B\).
\(M \models \mathsf{SU} A\)	iff	\(M \models \mathsf{PE} A \wedge \mathsf{MI} \neg A\).
\(M \models \mathsf{IN} A\)	iff	\(M \models \neg \mathsf{SI}A\).

Task 3. Check whether the following principles hold in McNamara’s system. If so, give an argument, if not, present a counter-model. I give two examples for items 1 and 2 below.

\(\mathsf{OP}p \leftrightarrow \mathsf{IN} p\)
\(\mathsf{IN}p \rightarrow \mathsf{OP}p\)
\(\mathsf{SU} p \rightarrow \neg \mathsf{OB} p\)
\(\mathsf{SU} p \rightarrow \mathsf{SU}(p \wedge q)\)
\((\neg \mathsf{MI} p \wedge \mathsf{PE} p) \rightarrow \mathsf{SU}p\)
\(\bigl( \mathsf{OB}(p \rightarrow q) \wedge \mathsf{OB}(q \rightarrow s) \wedge \mathsf{IN}p \wedge \mathsf{IN} s \bigr) \rightarrow \mathsf{IN} q\)
\(\bigl( \mathsf{OB}(p \rightarrow q) \wedge \mathsf{OB}((p \wedge q) \rightarrow s) \wedge \mathsf{IN}p \wedge \mathsf{IN} s \bigr) \rightarrow \mathsf{IN} q\)

Ad 1

This does not hold. We give an example with three worlds \(W= \{w_1, w_2, w_3\}\) for which

world	\(w_1\)	\(w_2\)	\(w_3\)
\(p\)	1	1	0

and the worlds are ordered as follows (skipping arrows from worlds to worlds that are equally ranked, e.g., loops; an arrow \(w_3 \rightarrow w_1\) means that \(w_3\ge w_1\)):

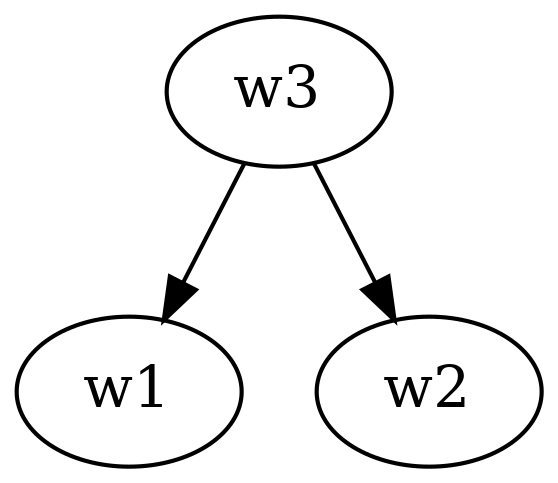
Note that we have \(M \models \mathsf{OP} p\) since there are two words \(w_1\) and \(w_3\) for which \(M,w_1 \models p\) while \(M,w_3 \models \neg p\).
Nevertheless, we don’t have \(M \models \mathsf{IN} p\) since we have a level of equally ranked worlds consisting of \(\{w_1, w_2\}\) such that all worlds in this level validate \(p\).

Ad 2

This does hold. Here is a proof. Suppose \(M = \langle W, \ge, v \rangle\) is a model and suppose \(M \models \mathsf{IN}p\). This means that for any \(w \in W\) there is a \(w^{\prime}\) for which \(w \ge w^{\prime}\) and \(w^{\prime} \ge w\), and

if \(M,w \models p\) then \(M,w^{\prime}\models \neg p\) and
if \(M,w \models \neg p\) then \(M,w^{\prime} \models p\).

Since \(W\) is non-empty, there is a world \(w \in W\).

Suppose \(M,w \models p\). Then there is a \(w^{\prime}\) for which \(M,w^{\prime} \models \neg p\) by item 1. Thus \(M \models \mathsf{OP} p\). (Recall, that a model validates \(\mathsf{OP}p\) if there are \(w_1, w_2 \in W\) for which \(M,w_1 \models p\) and \(M,w_2 \models \neg p\).)
Suppose \(M,w \models \neg p\). Then there is a \(w^{\prime}\) for which \(M,w^{\prime} \models p\) by item 2. Thus, \(M \models \mathsf{OP}p\).

Other solutions

Ad 3

This holds. To show this suppose \(M = \langle W, \le , v \rangle\) is an arbitrary model for which \(M \models \mathsf{SU} p\). Thus, by the definition of \(\mathsf{SU}\), \(M \models \mathsf{MI} \neg p\). Thus, there is a world \(w\) for which \(M,w \models \neg p\) and so \(M \models \neg \mathsf{OB} p\).

Ad 4

This does not hold in general. We give a counter-model \(M = \langle \{w_{1}, w_2\}, \ge, v \rangle\) where \(w_1 > w_2\) and

world	\(p\)	\(q\)
\(w_1\)	0	0
\(w_2\)	1	0

The \(M \models \mathsf{SU}p\) since \(M \models \mathsf{MI} \neg p\) and \(M \models \mathsf{PE} p\). However, it is not the case that \(M \models \mathsf{SU}(p \wedge q)\) since it is not the case that \(M \models \mathsf{PE}(p \wedge q)\).

Ad 5

This does not hold in general. We give a counter-model \(M = \langle \{ w_1, w_2 \}, \ge, v \rangle\) where \(w_1 \ge w_2\) and \(w_2 \ge w_1\) and

world	\(p\)
\(w_1\)	0
\(w_2\)	1

It is not the case that \(M \models \mathsf{MI}\neg p\) and therefore it is also not the case that \(M \models \mathsf{SU}p\). Note that it would not be intuitive in this model that \(p\) is supererogatory: there are no non-minimal worlds and so bringing about \(p\) is clearly not “beyond morality’s call”.

Ad 6

This holds. To show this we consider an arbitrary models \(M = \langle W, \ge, v \rangle\) for which \(M \models \mathsf{OB}(p \rightarrow q)\), \(M \models \mathsf{OB}(q \rightarrow s)\), \(M \models \mathsf{IN} p\) and \(M \models \mathsf{IN} s\). In order to show that \(M \models \mathsf{IN}q\), we have to show that for any \(w \in W\) there is a \(w_1, w_2 \in W\) such that

\(w_1 \ge w\), \(w \ge w_1\), and \(M,w_1 \models q\), and
\(w_2 \ge w\), \(w \ge w_2\), and \(M,w_2 \models \neg q\).

Let \(w \in W\) be arbitrary.

Since \(M \models \mathsf{IN}p\), there is a \(w_1 \in W\) for which \(w \ge w_1\) and \(w_1 \ge w\) and \(M,w_1 \models p\).
Since \(M \models \mathsf{OB}(p \rightarrow q)\), also \(M,w_1 \models q\).
Since \(M \models \mathsf{OB}(q \rightarrow s)\) also \(M,w_1 \models s\).
Since \(M \models \mathsf{IN} s\), there is a \(w_2 \in W\) for which \(w \ge w_2\), \(w_2 \ge w\) and \(M,w_2 \models \neg s\).
Since \(M \models \mathsf{OB}(q \rightarrow s)\) also \(M,w_2 \models \neg q\) (by Modus Tollens).

Since we have found our \(w_1\) and \(w_2\) our proof is finished.

Ad 7

This does not in general hold. We give a counter-model \(M = \langle W, \ge, v \rangle\) where \(W = \{ w_1, w_2\}\) and \(w_1 \ge w_2\) and \(w_2 \ge w_1\), and

models	\(p\)	\(q\)	\(s\)
\(w_1\)	1	1	1
\(w_2\)	0	1	0

Note that \(M \models \mathsf{OB}(p \rightarrow q)\), \(M \models \mathsf{OB} ((p \wedge q) \rightarrow s)\), \(M \models \mathsf{IN}p\) and \(M \models \mathsf{IN} s\) while it is not the case that \(M \models \mathsf{IN} q\).

This may come a bit as a surprise. McNamara’s example to motivate the Mares Principle (item 6) is as follows:

I here offer an example to help reveal its plausibility directly. Suppose that in return for numerous favors, I have promised to take you for a driving lesson some- time in the next few weeks and that to do so, I must arrange to borrow the family car (something I must not do too often). Then it is easy to imagine that I am obligated to act in such a way that: if I arrange to have the family car for next Friday (\(p\)), then I make the appointment to take you for a driving lesson next Friday (\(q\)); and if I make the appointment to take you for a driving lesson next Friday (\(q\)), then I show up at your place with the car next Friday (\(r\)). Suppose also that arranging to have the car for next Friday (\(p\)) and showing up with it at your place that day (\(r\)) are both (as of now) matters of indifference. Then it must also (as of now) be a matter of indifference whether I make the appointment with you for next Friday (\(q\)) or not. (p. 421)

Now, one could slightly adjust the middle piece by:

[…] and if I arrange to have the family car next friday (\(p\)) and make the appointment to take you for a driving lesson next Friday (\(q\)), then I show up at your place with the car next Friday (\(r\)) […]

What do you think, would this example motivate that item 7 should hold?

Another example to think about

Suppose we have:

where

world	email	call	dropby
\(w_1\)	0	0	1
\(w_2\)	0	1	0
\(w_3\)	1	0	0

In this case we get:

\(M \models \mathsf{SU} (\mathtt{call})\)
\(M \models \mathsf{SU} (\mathtt{dropby})\)
\(M \models \mathsf{SU}( \neg \mathtt{email})\)

While the former two are perfectly reasonable (= in alignment with our common sense usage of supererogation), the last item seems a bit odd. It holds since \(M \models \mathsf{MI}\neg\neg \mathtt{email}\) and \(M \models \mathsf{PE} \neg \mathtt{email}\).

What do you think: do you think this is as expected, does it align with your intuitions. If not, do you have an idea how to alter the semantic model to block this?

One of you suggested (please come forward, as always, I forgot the name: shame on me) to work also with sub-minimal worlds. In sub-ideal worlds both \(\mathtt{call}\) and \(\mathtt{dropby}\) will be false, and so will be \(\mathtt{email}\).

world	email	call	dropby
\(w_4\)	0	0	0

So, this may help us to demarcate actions/propositions that are functional in bringing about morally favourable states from those which don’t. Let \(M \models \mathsf{SUB} A\) iff \(A\) holds in all sub-minimal worlds. Then one could define \(M \models \mathsf{SU} A\) iff \(M \models \mathsf{MI}\neg A \wedge \mathsf{PE} A \wedge \neg \mathsf{SUB} A\). In our case we would get \(M \models \neg \mathsf{SU} \neg \mathtt{email}\) while we still get items 1 and 2.

However, one could easily imagine a sub-minimal world where \(\mathtt{email}\) is true: the world could by sub-minimal since another obligation is violated. In such a scenario also the proposed solution does not work.

Do you have other ideas?

References

McNamara, P. (1996). Making room for going beyond the call. Mind, 105(419), 415–450.
Mares, E. D., & McNamara, P. (1997). Supererogation in deontic logic: metatheory for DWE and some close neighbours. Studia Logica, 59(3), 397–415.

We here follow the somewhat simplified semantics from the article in Mind. In Mares & McNamara (1997) you can find a more refined characterization with all the meta-theory. ↩︎
We skip the clauses for the truth conditions for non-modal formulas. They are defined inductively as usual. (E.g., \(M,w \models A \wedge B\) iff \(M,w \models A\) and \(M,w \models B\).) ↩︎