Session 8: Seeing to it that …

Time for another fun blog entry … and it is indeed finally time to cover time and when we’re already at it to throw some agency in it as well.

In our last session, Michael Kesselheim gave a very nice presentation on stit-logic based on John Horty’s splendid book from 2001. In what follows, I will capture the most important insights from this session (typos and mistakes in this post are my responsibility, not his!).

When thinking about time we usually distinguish between the past, the present and the future, ending up with a time-line like this:

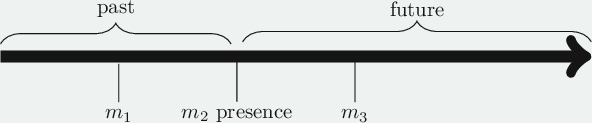\(m_2\) is the present moment in this picture, all moments to the left of \(m_2\), such as \(m_1\) are in the past, those to the right, such as \(m_3\) are in the future. Thus, one may think of a string of moments where the present moment plays the special role of demarcating the past from the future.

Especially in the context of human agency one may object to a deterministic picture according to which every moment comes with a uniquely determined future. For instance, to render our agents blameworthy and responsible for their actions we may require that they have the freedom to choose among different actions and their choices are not pre-determined. Needless to say, it is major challenge to coherently capture this moral desideratum within a naturalist understanding of human biology. But this need not bother us in this entry … For us the challenge will be rather to provide a logical framework in which we can reason about indeterministic time. Building on our simple picture above, we may thus introduce joints at moments where history divides into different possible courses, resulting in a tree-like structure of moments. And since trees grow from bottom to top we rotate things by -90 degrees:

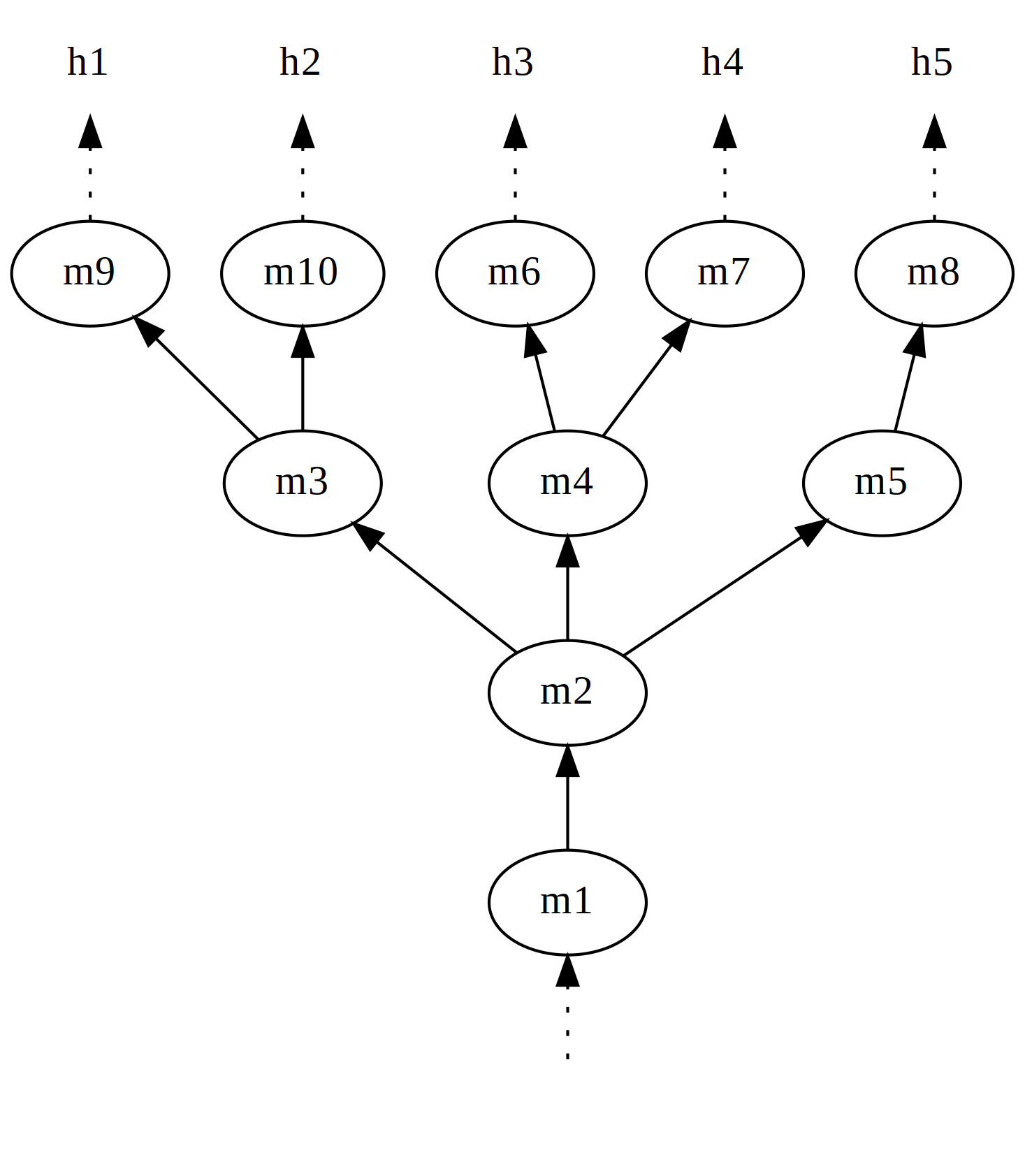
Consider, for instance, moment \(m_2\). History divides at this moment into three subsequent paths which themselves divide further as history unfolds itself. Talking about history, we have many alternative possible histories in our tree: each branch (i.e., each maximal linear sequence of moments) determines one history. E.g., history \(h_1 = \langle \ldots, m_{1}, m_2, m_3, m_9, \ldots \rangle\).

Time to mathematize our picture! A branching time frame is a structure \(\langle \mathtt{Moments}, < \rangle\) where \(<\) (“before”) is a binary relation on \(\mathtt{Moments}\) that is irreflexive, transitive, serial, and satisfies:

for all \(m_1, m_2, m_3 \in \mathtt{Moments}\), if \(m_1 < m_3\) and \(m_2 < m_3\), then \(m_1 = m_2\) or \(m_1 < m_2\) or \(m_2 < m_1\).

The last requirement makes sure that every moment \(m\) has a unique past history: any moment \(m^{\prime}\) past \(m\) (so: \(m^{\prime} < m\)) is part of every history going through \(m\). This is exactly where our tree-like structure comes from.

But enough talk about graphical representations of time: we want to do logic and thus we want to reason with and about time. Since things get usually complicated quickly in logic, we better start with a simple language, that of propositional logic, and supplement it with some modal operators to express facts about the past and the future. For instance,

\(\mathbb{P} A\) to express that at some past moment \(A\); or
\(\mathbb{F} A\) to express that at some future moment \(A\).

For instance, this way we can express that if \(A\) then it will be that \(A\) was the case. So: \(A \rightarrow \mathbb{F} \mathbb{P} A\).

Now, when incorporating interpretations of our formal language into our indeterministic time frames we have to be cautious when defining truth conditions. We have two ingredients, moments and history, and temporal statements seem to be context-dependent both on the moment and on the history. While the former is rather obvious, e.g., at this moment I sit on the balcony and type the blog while at a soon to come future moment this will not anymore be the case since I will make pizza. Wait, that is, in one particular future history I will stick to this plan, there may be another history in which I change my mind and rather be content with a pack of vegan fast food ramen (typing this blog entry already takes way too much of my time anyway!). So, “I will make pizza” is at the present moment true relative to the former history, but not relative to the latter history.

These consideration motivate to evaluate formulas not at moments only, but rather at pairs of moments and histories. Wrapping up things in a mathematical way we thus define a branching time model \(M\) as a triple \(\langle \mathtt{Moments}, <, v \rangle\) where \(\langle \mathtt{Moments}, < \rangle\) is an indeterministic time frame and \(v\) is an assignment function that associates each moment-history pair \(m/h\) and each atomic formula \(A\) with a truth value \(0\) or \(1\). For this we need only consider moment-history pairs \(m/h\) where \(m\) is contained in \(h\). We will write \(H_m\) for the set of all histories that “go through” \(m\). We then define truth of a formula at a moment-history pair pretty much as expected:

\(M, m/h \models A\) where \(A\) is an atomic formula, iff, \(v(m/h, A) = 1\).
\(M, m/h \models \neg A\) iff not(\(M, m/h \models A\)).
\(M, m/h \models A \wedge B\) iff \(M,m/h \models A\) and \(M,m/h \models B\).
etc. for other connectives.
\(M, m/h \models \mathbb{P} A\) iff there is a \(m^{\prime} \in h\) such that \(m^{\prime} < m\) and \(M, m^{\prime}/h \models A\).
\(M, m/h \models \mathbb{F} A\) iff there is a \(m^{\prime} \in h\) such that \(m < m^{\prime}\) and \(M, m^{\prime}/h \models A\).

One may define dual operators based on \(\mathbb{P}\) and \(\mathbb{F}\) as usual:

\(\mathbb{H}A =_{\mathsf{df}} \neg \mathbb{P}\neg A\): it has always been the case that \(A\).
\(\mathbb{G}A = _{\mathsf{df}} \neg\mathbb{F}\neg A\): it will always be the case that \(A\).

This is a splendid moment for some exercises for you, while I make some pizza.

Excercises 1. Do the following formulas hold in any model \(M = \langle \mathtt{Moments}, <, v \rangle\), at any moment \(m \in \mathsf{Moments}\) and history \(h \in H_m\)? If not, find a counter-example, if yes, give a short reason.

\(M, m/h \models A \rightarrow \mathbb{F}\mathbb{P}A\)

\(M, m/h \models \mathbb{G}A \rightarrow \mathbb{F}A\)

\(M, m/h \models \mathbb{F} A \rightarrow \mathbb{G} \mathbb{F} A\)

Task 1.
1. Suppose \(M, m/h \models A \rightarrow \mathbb{F} \mathbb{P} A\).
2. By the seriality of \(<\) there is a \(m^{\prime}\) such that \(m < m^{\prime}\).
3. By 1 and 2, \(M, m^{\prime}/h \models \mathbb{P} A\).
4. By 2 and 3, \(M, m/h \models \mathbb{F} \mathbb{P} A\).
Task 2.
1. Suppose \(M, m/h \models \mathbb{G} A\).
2. By the seriality of \(<\) there is a \(m^{\prime}\) such that \(m < m^{\prime}\).
3. By 1 and 2, \(M, m^{\prime}/h \models A\).
4. By 2 and 3, \(M, m/h \models \mathbb{F} A\).
Task 3.
1. Let \(\mathsf{Moments} = \{ m_1, m_2, \ldots \}\). Let \(<\) be such that \(m_i < m_j\) iff \(i < j\). We have exactly one history, \(h = \langle m_{1}, m_2, \ldots \rangle\). Let \(v(m_1/h, p) = v(m_2/h, p ) = 1\) and \(v(m_i/h, p) = 0\) for all \(i \ge 3\).
2. We have: \(M, m_1/h \models \mathbb{F}p\) since \(m_1 < m_2\) and \(M, m_2/h \models p\).
3. At the same time: \(M, m_2/h \models \neg \mathbb{F} p\) since for all \(m_i\) for which \(m_2 <m_i\), \(M, m_i/h \models \neg p\).
4. So, \(M, m_1/h \not\models \mathbb{G} \mathbb{F} p\).

Our framework allows us also to define a notion of “momentarily being settled”: the idea is that \(A\) is settled at the moment \(m\) iff it is true relative to any history that goes through \(m\):

\(M, m/h \models \Box A\) ("\(A\) is settled at \(m/h\)") iff for all \(h^{\prime} \in H_m\), \(M,m/h^{\prime} \models A\).

We then define the dual \(\Diamond\) in the usual way:

\(\Diamond A =_{\mathsf{df}} \neg \Box \neg A\)

This allows us to give a little twist to our previous exercises.

Exercises 2. Do the following formulas hold in any model \(M = \langle \mathtt{Moments}, <, v \rangle\), at any moment \(m \in \mathsf{Moments}\) and history \(h \in H_m\)? If not, find a counter-example, if yes, give a short reason.

\(M, m/h \models \Box A \rightarrow \mathbb{F} \Box \mathbb{P} A\)

\(M, m/h \models A \rightarrow \Box\mathbb{F} \mathbb{P} A\)

\(M, m/h \models \Box A \rightarrow \Box \mathbb{P} \mathbb{F} A\).

Task 1.
1. Suppose \(M, m/h \models \Box A\).Thus, for every \(h^{\prime} \in H_m\), \(M, m/h^{\prime} \models A\).
2. By the seriality of \(<\) and the definitions of histories (as maximal sequence of successive moments), there is a \(m^{\prime}\) for which \(m < m^{\prime}\) and \(h \in H_{m’}\).
3. Let \(h^{\prime} \in H_{m^{\prime}}\). We have \(M, m^{\prime}/h^{\prime} \models \mathbb{P}A\) since \(m<m^{\prime}\) and \(M, m/ h^{\prime} \models A\) (by 1).
4. Since 3 holds for any \(h^{\prime} \in H_{m^{\prime}}\) and \(h \in H_{m’}\), \(M, m^{\prime}/h \models \Box \mathbb{P}A\).
5. Hence, \(M, m/h \models \mathbb{F} \Box \mathbb{P}A\).
Task 2. We define a counter-model as follows (where \(A = p\)):
1. \(\mathtt{Moments}= \{ m_{0} \} \cup \{m_1, m_2, \ldots \} \cup \{ m_1^{\prime}, m_2^{\prime}, \ldots \}\).
2. Let \(<\) be such that \(m_{0} < m^{\prime}\) for all \(m^{\prime} \in \mathsf{Moments}\) for which \(m_0 \neq m^{\prime}\). Moreover, let \(m_i < m_j\) iff \(i < j\) and \(m_i^{\prime} < m_j^{\prime}\) iff \(i < j\). So we get V-shaped structure with \(m_0\) at its tip. We have two histories through \(m_0\), namely \(h_{\mathsf{left}} = \langle m, m_{1}, m_2, \ldots \rangle\) and \(h_{\mathsf{right}}{\prime} = \langle m, m_{1}^{\prime}, m_2^{\prime}, \ldots \rangle\).
3. Let \(v\) be such that for all moments \(m^{\prime} \in \mathsf{Moments}\) we have \(v(m^{\prime}/h_{\mathsf{left}}, p) = 1\) and \(v(m^{\prime}/h_{\mathsf{right}}, p) = 0\).
4. So, we have:
  1. \(M, m_0/h_{\mathsf{left}} \models p\) while \(M, m_{0} / h_{\mathsf{right}} \models \neg p\).
  2. Furthermore, \(M, m_i^{\prime}/h_{\mathsf{right}} \models \mathbb{P}\neg p\) for all \(i \ge 1\), and \(M, m_i^{\prime}/h_{\mathsf{right}} \not \models \mathbb{P} p\).
  3. By 2 and the definition of \(<\), \(M, m_{0}/h_{\mathsf{right}} \models \neg \mathbb{F}\mathbb{P} p\).
  4. So, \(M,m/h_{\mathsf{left}}\models \neg \Box \mathbb{F} \mathbb{P} p\) although \(M, m_{0}/h_{\mathsf{left}} \models p\).
Task 3. A counter-model is given by \(\mathsf{Moments} = \{ m_1, m_2, \ldots \}\) where \(m_i < m_j\) iff \(i < j\). Note that there is exactly one history \(h = \langle m_{1}, m_2, \ldots \rangle\). Let \(v(m_i/h,p) = 1\) for all \(i \ge 1\).
- We then have: \(M, m_1/h \models \Box p\), but \(M, m_1/h \not\models \mathbb{P} A\) for any \(A\) for the simple reason that there is no predecessor moments to \(m_1\).
- Note that the situation would be different is we were to request that \(<\) warrants that for every moments there is a predecessor moment.

Now that we have a good grip on timelines, let us infuse some agency into our story. How do we do that? First, we need some protagonists, a set \(\mathtt{Agents}\), and second, and most importantly and more challenging: in any reasonable story agents make good and often bad choices. How to best think of choices in the context of moments and histories? As usual, we simplify several aspects. First, we only consider choices which are instantaneous: they happen in an instance at a given moment without having any duration. Second, observe that in the indeterministic model of time, every choice I make as a free agent forces the path of history in a specific direction. Having decided to write the blog article instead of jogging at moment \(m\) did cut off possible futures where I right now am jogging (talking about bad choices again …) and narrowed down the bundle of possible histories to those consistent with the fact that I am right now writing this blog article.

Let us formalize this idea along the following observations:

Moments come with bundles of histories which go through them. In our example we have histories \(h_1, \ldots, h_5\) going through \(m\):
Different choices exclude different histories. In that sense they partition the currently available bundle of histories. In the example below my choices at \(m\) partition \(H_m\) into \(\{ \{ h_1, h_2 \}, \{ h_3, h_4 \}, \{ h_5 \} \}\). Mathematically speaking, a partition of a set \(X\) is a set of non-empty subsets \(X_1, \dotsc, X_n\) of \(X\) which are mutually non-intersecting (ie., \(X_i \cap X_j = \emptyset\) for all \(1 \le i < j \le n\)) and together cover whole of \(X\) (ie., \(X_1 \cup \cdots \cup X_n = X\)). ¹

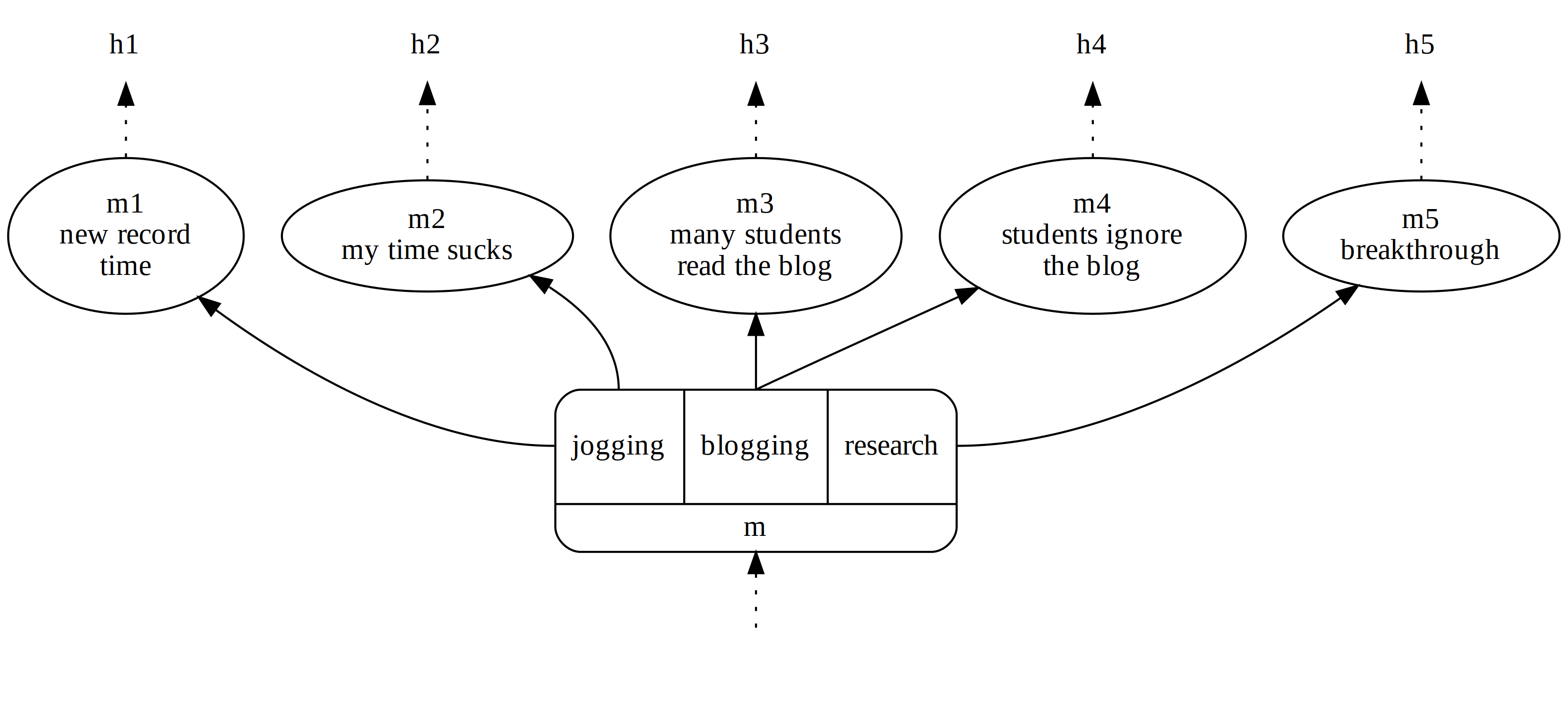Note that in the graph I used “flavor texts” (jogging, blogging and research) for the available choices. Mathematically though, they are just non-empty sets of histories: \(\mathtt{jogging} = \{ h_1, h_2 \}\), etc.
We also observe that my choices are typically not forceful enough to narrow down history to a unique course. E.g., whether I get a new record time when jogging may also depend on the weather besides my effort and previous training. So, with my current choices I may not be able to enforce history \(h_1\). Similarly, it may be beyond my current influence whether students will read the blog entry since that will depend on your rather than my choices.
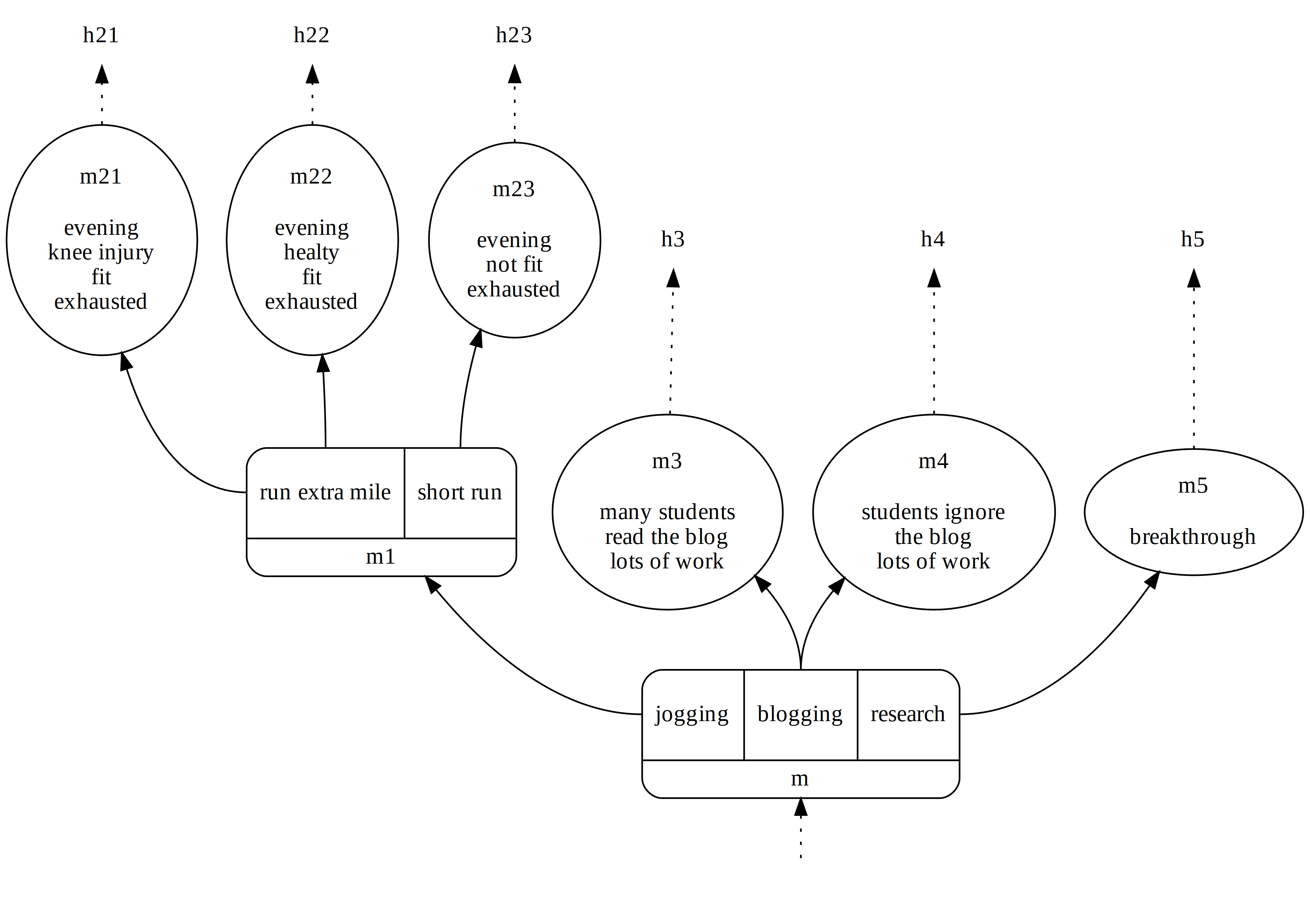
Also, my current choices should not have the power to differentiate between histories that are being forked only in the future. E.g., whether I will be fit or not fit depends on my later choice at \(m_1\) whether I run the extra mile. My current decision whether to jog or rather blog or research cannot yet influence this. So any partition/choice that separates e.g., \(h_{22}\) from \(h_{23}\) is not possible at moment \(m\).
In sum, we add two ingredients to our frames:
1. A (non-empty) set \(\mathtt{Agents}\) of agents.
2. A function \(\mathsf{choice}\) that takes as input an agent \(\alpha \in \mathtt{Agents}\) and a moment \(m \in \mathtt{Moments}\) and outputs a partition of \(H_m\). We follow Horty and write \(\mathsf{choice}_{\alpha}^m\) instead of \(\mathsf{choice}(\alpha, m)\).This is also a good opportunity to introduce another notation: \(\mathsf{choice}_{\alpha}^m(h)\) (where \(h \in H_m\)) is the choice of agent \(\alpha\) at moment \(m\) that includes the history \(h\). Since \(\mathsf{choice}_{\alpha}^m\) outputs a partition of \(H_m\), there is a unique “cell” in which \(h\) is contained.
  
  And our new structures shall also get a name: stit frames and stit models.
Wait, you will say, “stit?!”, what kind of name is that. And also, you may wonder, when we will finally talk about the “Seeing to it …” from the title of this entry? Now is the time! What does it mean that an agent \(\alpha\) at a moment \(m\) relative to a history \(h\) sees it to it that \(A\)? If you made it through this entry so far, there is a good chance you will agree that it means that the choice that \(\alpha\) makes in at \(m\) relative to \(h\), i.e., \(\mathsf{choice}_{\alpha}^m(h)\), warrants that \(A\) holds. More formally, we use an operator \(\mathsf{cstit}\) (“stit”: seeing to it that, aha!) and (“c” for the logician Chellas):
- \(M, m/h \models [\alpha~ \mathsf{cstit}{:}~ A]\) iff for all \(h^{\prime} \in \mathsf{choice}_{\alpha}^m(h)\), \(M, m/h^{\prime} \models A\).
In our example above, we have, for instance:
- \(M, m/h_3 \models [\alpha ~ \mathsf{cstit}{:}~\mathbb{F}~ \mathtt{lots{-}of{-}work}]\) since
  - \(\mathsf{choice}_{\alpha}^m(h_3) = \{ h_3, h_4 \}\),
  - \(M, m/h_3 \models \mathbb{F}~ \mathtt{lots{-}of{-}work}\), and
  - \(M, m/h_4 \models \mathbb{F} ~ \mathtt{lots{-}of{-}work}\)
- However, we don’t have: \(M, m/h_3 \models [\alpha~ \mathsf{cstit}{:} ~ \mathbb{F}\mathtt{many{-}students{-}read{-}the{-}blog}]\) since
  - \(h_4 \in \mathsf{choice}_{\alpha}^m(h_3)\) and
  - we don’t have: \(M, m/h_4 \models \mathbb{F}~ \mathtt{many{-}students{-}read{-}the{-}blog}\).

Exercise 2.5. Show that \([\alpha ~\mathsf{cstit{:}}~ A]\) is equivalent to \([\alpha ~\mathsf{cstit{:}}~ [\alpha ~\mathsf{cstit{:}}~ A]]\).

Suppose first that \(M, m/h \models [\alpha ~\mathsf{cstit{:}}~ A]\).
1. Thus, for all \(h’ \in \mathsf{choice}_{\alpha}^m(h)\), \(M, m/h’ \models A\).
2. We have to show that for all \(h’ \in \mathsf{choice}_{\alpha}^m(h)\), \(M, m/h’ \models [\alpha ~\mathsf{cstit{:}}~ A]\).
3. This holds if for all \(h’’ \in \mathsf{choice}_{\alpha}^m(h’)\), \(M, m/h’’ \models A\).
4. But note that for all \(h’ \in \mathsf{choice}_{\alpha}^m(h)\), \(\mathsf{choice}_{\alpha}^m(h) = \mathsf{choice}_{\alpha}^m(h’)\) (since every history belongs to a unique choice “cell”).
5. Thus, item 3 follows from item 1 which completes our proof.
Suppose now that \(M, m/h \models [\alpha ~\mathsf{cstit{:}}~ [\alpha ~\mathsf{cstit{:}}~ A]]\).
1. Thus, for all \(h’ \in \mathsf{choice}_{\alpha}^m(h)\), \(M, m/h’ \models [\alpha ~\mathsf{cstit{:}}~ A]\).
2. Since \(h \in \mathsf{choice}_{\alpha}^m(h)\), \(M, m/h \models [\alpha ~\mathsf{cstit{:}}~ A]\),which completes our proof.

Excercises 3. Which of the following statements hold?

\(M, m/h_{22} \models [\alpha~ \mathsf{cstit}{:}~ \mathbb{F} ~ \mathtt{fit}]\).

\(M, m/h_{22} \models [\alpha~ \mathsf{cstit}{:}~ \mathbb{F}\Box\mathtt{exhausted}]\).

\(M, m/h_{22} \models [\alpha~ \mathsf{cstit}{:}~ [\alpha~ \mathsf{cstit}{:} ~ \mathbb{F} ~ \mathtt{fit}]]\)

\(M, m/h_{22} \models [\alpha~ \mathsf{cstit}{:}~ [\alpha~ \mathsf{cstit}{:} ~ \mathbb{F} ~ \mathtt{exhausted}]]\)

\(M, m_1/h_{22} \models [\alpha ~ \mathsf{cstit}{:} ~ \mathbb{F} ~ \mathtt{fit}]\)

We assume that in \(m_1\) it is not true that evening, healthy, fit and exhausted and that the fitness state doesn’t change to the positive every \(m_{23}\).

Nope. The reason is that \(M, m_{23}/h_{23} \models \neg \mathtt{fit}\) and \(h_{23} \in \mathsf{choice}_{\alpha}^m(h_{22})\).
Yay. The reason is that \(M,m_1/h \models \Box \mathtt{exhausted}\) for all \(h \in \{ h_{21}, h_{22}, h_{23} \} = \mathsf{choice}_{\alpha}^m(h_{22})\) and \(m < m_1\).
Nope. The reason is that this statement is equivalent to the one in Item 1 (as shown in exercise 2.5).
Yay. Similar reason to 2.
Yay. The reason is that \(M, m_{22}/h_{22} \models \mathtt{fit}\) and \(M, m_{21}/h_{21} \models \mathtt{fit}\) and \(m_1 < m_{22}\) and \(m_1 < m_{21}\) and \(\mathsf{choice}_{\alpha}^{m_1}(h_{22}) = \{ h_{22}, h_{21} \}\).

In the next session we will learn more about stit, including a variant \(\mathsf{dstit}\), and how to model “refraining from …” within our framework. And then we will have finally all the tools to come back to our main plot-line: deontic logic and normative reasoning. Yet again, we will see that there are quite some subtleties involved when integrating obligations in a stit-framework! So, stay tuned … and see it to it that you join us on Tuesday.

Resources

Horty, J. F. (2001). Agency and deontic logic. Oxford University Press.
As always I recommend the Stanford Encyclopedia entry on Temporal Logic (Stanford Encyclopedia of Philosophy).

Before you protest: yes, a partition may also have infinitely many members. ↩︎