Vor einigen Jahren startete die US-Regierung das SETI-Projekt (Search for ExtraTerrestrial Intelligence - Suche nach außerirdischen Intelligenzen). Mit riesigen Radioteleskopen wurde der Himmel abgesucht, in der Hoffnung, ein Radio-, Funk- oder gar TV-Signal einer anderen Zivilisation aufzufangen. Wer den Film "Contact" gesehen hat, weiß, wie der Traum der Mitarbeiter aussah(?).

Vor einiger Zeit nun drehte die Regierung auf Grund mangelnder Ergebnisse und Nutzen den Geldhahn zu. Das gesamte Projekt stand vor dem Aus. Die Messungen gingen zwar weiter, jedoch gab es nicht mehr genug Mitarbeiter und Rechner, um die empfangenen Signale auszuwerten. Da aber kam man auf die geniale Idee, die weltweite Rechenkapazität des Internets zu nutzen. Überall auf der Welt, in Büros, Unis und auch im Privatgebrauch liefen Computer täglich mehrere Stunden, nur um Strom zu verbrauchen und Sterne, Fenster oder Toaster fliegen zu lassen. Diese Zeit, in der der Rechner nicht benötigt wird, aber trotzdem läuft, wollte man zur Auswertung nutzen. Also programmierte man kurzer Hand einen Bildschirmschoner, der Daten aus dem Netz holen, sie durchrechnen und wieder zurückschicken kann. Am 17. Mai 1999 startete dann dieses bisher einmalige Projekt, genannt SETI@home (SETI zu Hause).

Das Programm, erhältlich für so ziemlich alle Betriebssysteme, hat unter Windows nur ca. 700K, unter Linux gar nur 70K. Ein Datensatz ist ca. 350K groß, und die Rechenzeit beträgt zwischen 4h (moderner Alpha) und 250h (alter 486er). Der Pentium-Schnitt mit Windows liegt bei 50h. Wenn man das Programm nicht als Bildschirmschoner laufen läßt, sondern als eigene und alleinige Anwendung, benötigt ein PII600 8-10h, je nach Betriebssystem und Arbeitsspeicher. Ein kleiner Tip: Die Einstellung "Blank Screen" beschleunigt das ganze ca. um den Faktor zwei.

Welche physikalischen Grundlagen hat die Berechnung? - Das Teleskop ist im Prinzip nichts anderes als eine überdimensionale Radioantenne, ähnlich wie das Radio (z.B. 106.7Mhz) auf einen festen "Sender" (ca. 1.4Ghz) eingestellt. Diese Frequenz entspricht dem 21cm-Band, hier haben Wissenschaftler die größte Wahrscheinlichkeit für Erfolg vorhergesagt.
Wie sehen die Berechnungen aus? - Hört man sich das Signal an, ist nur ein Rauschen zu hören, da sich hier viele Wellenlängen überlagern, ähnlich den Farben, die zusammengemischt weiß ergeben oder einem Ton auf dem Klavier, der ja auch viele Ober- und Unterschwingungen enthält. Das Programm geht nun hin und zerlegt die Trägerfrequenz (eben 1.41Ghz) mittels einer Fourriertransformation (in manchen Büchern Fourier) in die darin enthaltenen Unterfrequenzen/-wellen. Zusätzlich ist auch unbekannt, welche Bandbreite ein mögliches Signal hat. Also geht das Programm noch hin und probiert einfach mehrer wahrscheinliche Werte aus. Ein weiteres Problem ist der sogenannte Doppler-Effekt. Er bewirkt z.B. daß eine sich nähernde Lokomotive höher pfeifft als eine sich entfernende. Beim irdischen Radio hat dieser Effekt kaum Auswirkungen, unsere Autos sind einfach zu langsam. Da sich die Planeten aber um einiges schneller bewegen, wird das Signal doch sehr stark verzerrt. Auch hier probiert der Rechner einfach eine Reihe von wahrscheinlichen Werten aus. Hat er ein starkes oder, noch besser, ein wiederkehrendes Signal gefunde, wird dies vermerkt und später abgeschickt.

Was ist Fourriertransformation (!Techbabble!)? - Jede Funktion, periodisch oder nicht, also auch ein Rauschen, läßt sich durch eine solche Transformation in ein Integral (=Summe) aus Sinus-Funktionen zerlegen.
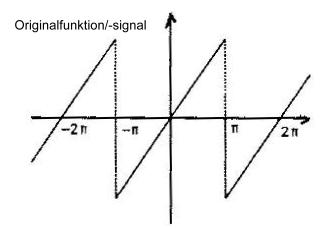Sinus-Funktionen sind physikalisch "reine" Töne, außerdem kann man mit ihnen sehr gut rechnen. Ähnlich der Transformation, aber deutlicher einsehbar ist die Fourrier-Reihe. Nimmt man unendlich viele Summanden, hat man die eigentliche Funktion. Geht man nur bis zu einer bestimmten Anzahl Summanden, ist der Rechenaufwand viel geringer, und das Ergebnis ist der Originalfunktion trotzdem noch ähnlich genug. Jeder Summand entspricht dabei einem Ton.

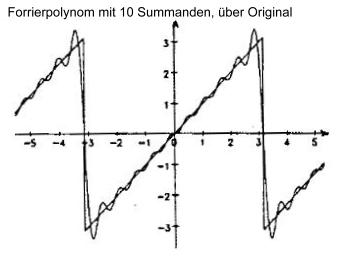
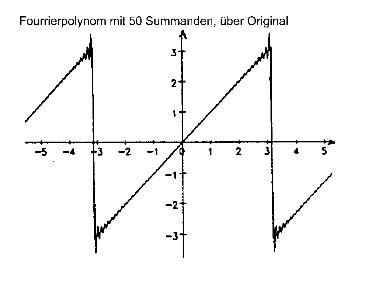Verwendet wird dieses Verfahren auch bei CD´s, oder MP3´s, wo die Töne (=Sinus-Funktionen), die der Mensch nicht hört, herausgenommen werden. Bleibt nur zu hoffen, daß das Programm auch wirklich das tut, was es soll und kein verkappter Virus ist, sonst würde ein solches Projekt wohl nie wieder funktionieren. Für das Programm spricht seine Herkunft (Berkeley.edu) und einige andere Hinweise (z.B. Verwendung von Mathematik-lib´s unter Linux). Ganz sicher kann man sich jedoch nicht sein, der Quellcode ist nicht zugänglich. Jeder der noch Fragen hat, die die Links nicht beantworten, kann mir ja mailen. Ansonsten sind alle eingeladen, unserem Team beizutreten.