Zur Homepage von Jörg Winkelmann  Zur Homepage zur Vorlesung

Mathematisches Institut der Universität Basel
Vorlesung Infinitesimalrechnung II (SS 2000)

PD Dr. Jörg Winkelmann

Aufgabenblatt 11

Abgabetermin: 30. Juni 2000

1.

Bestimme die globalen und lokalen Extrema der durch 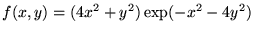gegebenen Funktion .

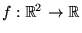2.

Sei f eine stetig differenzierbare Funktion auf und g(x)=sin(|f(x)|²) . Bestimme .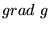

3.

Sei 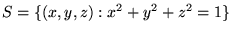, 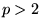und 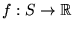gegeben durch f(x,y,z)=x^p+y^p+z^p . Bestimme Minima und Maxima von f auf S .

4.

Zeige, dass 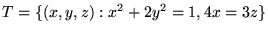kompakt ist und bestimme Maxima und Minima von f(x,y,z)=x+y-z auf T .

5.

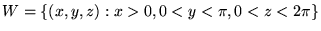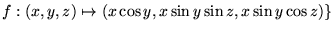Sei und . Bestimme das Bild f(W) und zeige, dass f ein Diffeomorphismus von W auf f(W) ist.

(*) 6.

Es sei 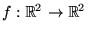gegeben durch f(x,y)=(y-x²)(y-2x²) . Zeige: f hat kein lokales Minimum in (0,0) , aber für jedes 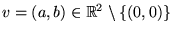besitzt die durch 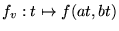definierte Funktion 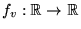ein lokales Minimum in 0 .