Zur Homepage von
Jörg Winkelmann
Zur Homepage zur
Vorlesung
Mathematisches Institut der Universität Basel
Vorlesung Infinitesimalrechnung I (SS 2000)
PD Dr. Jörg Winkelmann
Abgabetermin: 7. Juli 2000
- 1.
- Sei
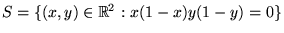 .
Skizziere S und zeige, dass es keine differenzierbare
Funktion
.
Skizziere S und zeige, dass es keine differenzierbare
Funktion 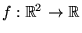 gibt mit
gibt mit 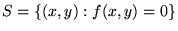 und
und 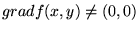 für alle
für alle 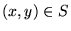 .
.
- 2.
- Seien
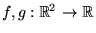 die durch f(x,y)=x2-y3 und
g(x,y)=-3y gegebenen Funktionen. Sei
die durch f(x,y)=x2-y3 und
g(x,y)=-3y gegebenen Funktionen. Sei 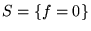 .
Bestimme globale Extrema von g|S und berechne
.
Bestimme globale Extrema von g|S und berechne
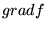 und
und 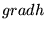 .
.
- 3.
- Für einen gegebenen Punkt
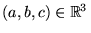 bestimme man die Ebene
E mit
bestimme man die Ebene
E mit 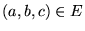 ,
für die der durch E und die Ebenen
,
für die der durch E und die Ebenen 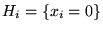 begrenzte
Tetraeder minimales Volumen hat.
begrenzte
Tetraeder minimales Volumen hat.
- 4.
- Sei
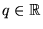 ,
,
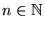 ,
,
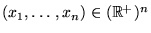 mit
mit 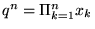 .
.
Zeige:
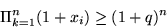
- 5.
- Seien
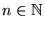 ,
,
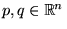 .
Sei S die Menge aller der Weglänge nach parametrisierten Wege von
p nach q und
.
Sei S die Menge aller der Weglänge nach parametrisierten Wege von
p nach q und 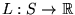 die Abbildung, die jedem Weg seine Länge
zuordnet. Bestimme, wo L auf S Minima annimmt.
die Abbildung, die jedem Weg seine Länge
zuordnet. Bestimme, wo L auf S Minima annimmt.
- (*) 6.
- Sei
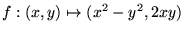 .
Zeige, dass es in einer Umgebung von (1,0) eine Umkehrabbildung für f
gibt, wähle eine solche Umgebung und bestimme explizit die
Umkehrabbildung (Tip: Beachte
.
Zeige, dass es in einer Umgebung von (1,0) eine Umkehrabbildung für f
gibt, wähle eine solche Umgebung und bestimme explizit die
Umkehrabbildung (Tip: Beachte 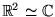 .)
.)
Joerg Winkelmann
2000-06-30
![]()
![]()