4. Regenübung:
Turmhöhenbestimmung
Inhalt
4.1. Erläuterung der Aufgabenstellung in eigenen Worten
4.2. Beschreibung des Meßverfahrens
4.3. Meßprotokolle mit Verprobung:
4.3.1 Zenitwinkel
4.3.2. Horiziontalwinkel
4.3.3. Höhennivellement
4.4. Auswertung der Beobachtungsdaten
4.4.1. Nivellement
4.4.2. Berechnung der Strecken
4.4.3. Turmeinzelhöhen
4.5. Statistik
4.5.1. Standardabweichung einer Einzelhöhe und des
arithmetischen Mittels
4.5.2. Standardabweichung des Nivellement
4.5.3. Horizontalwinkelmessung
4.5.4. Vertikalwinkelmessung
4.5.5. Standardabweichung der Strecken
4.5.6. Standardabweichung einer Einzelhöhe nach dem
Varianzfortpflanzungsgesetz
4.6. Abschließende beurteilende Stellungnahme
4.1. Erläuterung der Aufgabenstellung in eigenen Worten
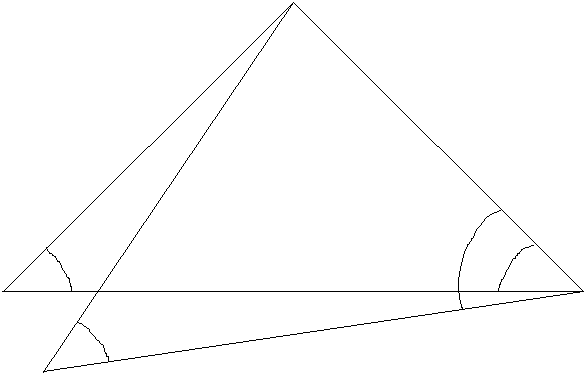
Es sollte in dieser Übung die Höhe des Kamins des Universitätsheizkraftwerkes bestimmt werden. Da der Fuß des Kamins nicht eindeutig angezielt werden konnte, zielten wir stattdessen eine Tafel an, die auf der Turmoberfläche genau 3 m über dem Boden befestigt war. Diesen Punkt nannten wir Tu, der Punkt an der Spitze wird im folgenden To (Turmoberkante) genannt. Aus der Differenz der NN-Höhen dieser beiden Punkte erhalten wir am Ende die gesuchte Höhe des Kamins. Die NN-Höhen errechnen sich trigonometrisch mit zwei horizontalen Hilfsdreiecken:
T

a1 a2 b1/2
b 1 c1 a 2 a 1
C A
b 2 c2
B
Um die NN-Höhen der Punkte zu bekommen, mussten die NN-Höhen der Meßstandpunkte ermittelt werden. Dies geschah mittels Nivellement von der bekannten Höhe des Bolzens am Trafohäuschen. Die Höhen wurden aus Hin- und Rückgang mit je einem WP ermittelt.
Als erster Schritt wurden die drei Punkte A, B und C festgelegt, auf denen anschließend die Stative aufgestellt werden sollten. Dies erwies sich teilweise als problematisch, da von allen Punkten eine freie Sicht auf die Punkte Tu und To gewährleistet werden musste, die Strecken aber teilweise durch Büsche und Sträucher verdeckt waren.
Bei der Anlage des Hilfsdreiecks sollte darauf geachtet werden, dass die Winkel
a i und b i zwischen den Strecken AB (c1) bzw. AC (c2) und AT ungefähr 50 gon betragen, um eine möglichst genaue Messung zu erzielen. Ferner sollten die Strecken c1 und c2 in ihrer Länge in etwa mit der Höhe des Turmes übereinstimmen.Nachdem die Hilfsdreiecke angelegt wurden, haben wir folgende Messungen mit dem elektr. Tachymeter durchgeführt:
Punkt A:
Zur Bestimmung der Höhe des Gerätes wurde ein Höhennivellement zum Festpunkt 100,00 durchgeführt. Zu den Punkten B, C und Tu wurden dann die Horizontal- und Zenitwinkel in zwei Vollsätzen gemessen. Zum Punkt To wurde nur der Zenitwinkel gemessen, weil der Horizontalwinkel identisch mit dem von Tu sein muss, da die Punkte lotrecht übereinander sind. Des weiteren wurden die Strecken c1 und c2 je viermal bestimmt und anschließend gemittelt.
Punkt B und C:
Von diesen Punkten werden jeweils die Horizontal- und Vertikalwinkel zu den Punkten Tu und A sowie der Zenitwinkel zum Punkt To gemessen.
4.3. Meßprotokolle mit Verprobung
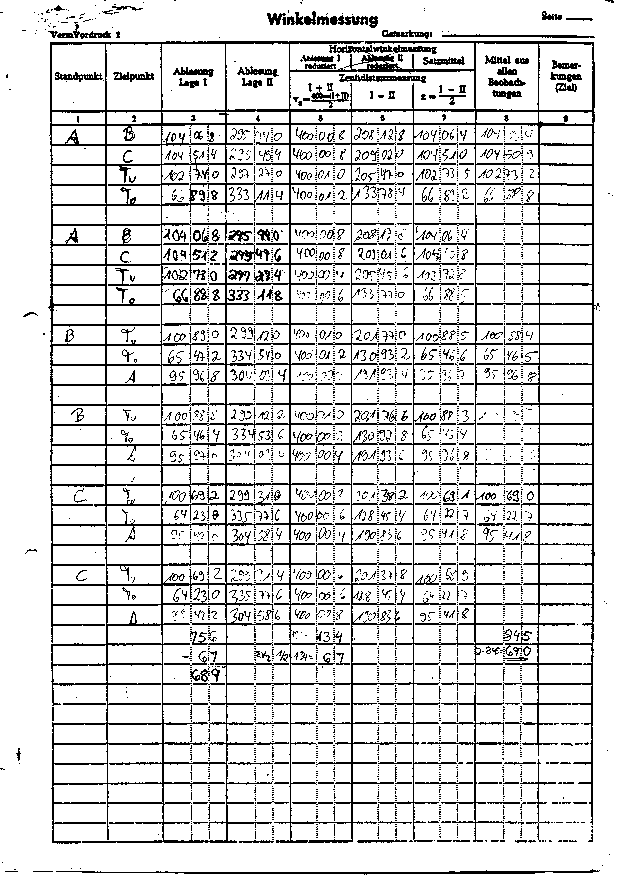 4.3.1. Zenitwinkel
4.3.1. Zenitwinkel
4.3.2. Horizontalwinkel

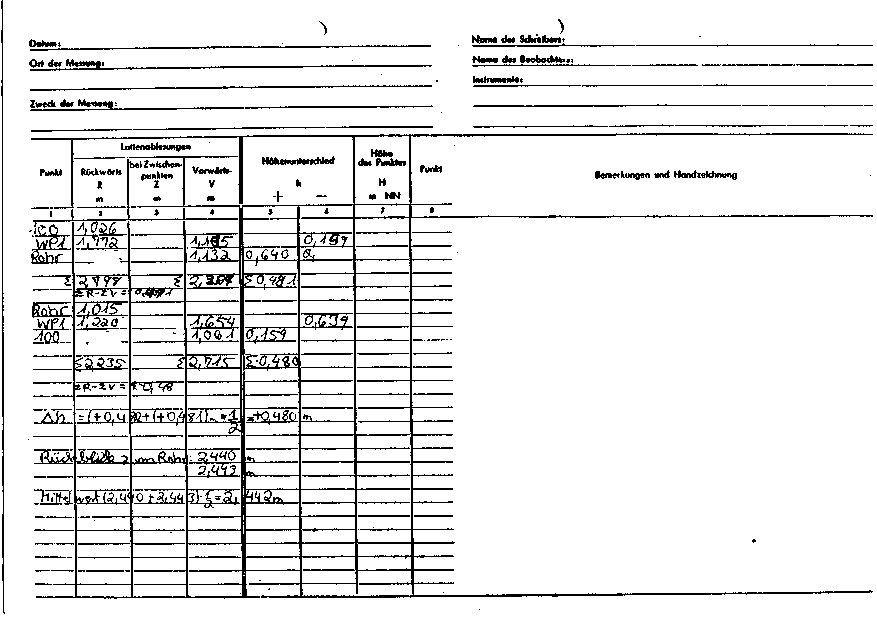 4.3.3. Höhennivellement
4.3.3. Höhennivellement
4.4. Auswertung der Beobachtungsdaten
4.4.1. Nivellement
Höhe von Gerätepunkt A
HA = Festpunkthöhe + Mittel der Höhenunterschiede vom Festpunkt zum Punkt O (Rohr) + Mittel der Höhenunterschiede aus den Rückblicken von Punkt C zu O
HA = 100,00m + ½*(0,480 + 0,481) + ½*(2,440 + 2,443) = 102,922
Höhe von Gerätepunkt B
C2 = AB * sin (Zenitwinkel von A zu B) = 35,341m * sin 104,064 = 35,359m
HB1 = HA + C2 * cot(A,B) = 102,922 + 35,359 * cot 104,064 = 100,662m
HB2 = HA – C2 * cot(B,A) = 102,922 – 35,359 * cot 95,968 = 100,680m
HB = ½ * (HB1 + HB2) = 100,671m
Höhe von Gerätepunkt C
C1 = AC * sin(A,C) = 34,656 * sin 104,509 = 34,569
HC1 = HA + C1 * cot(A,C) = 102,922 + 34,569 * cot 104,509 = 100,469m
HC2 = HA - C1 * cot(C,A) = 102,922 – 34,569 * cot 95,418 = 100,430m
HC = ½ * (HC1 + HC2) = 100,450m
4.4.2 Berechnung der Strecken
a
1 = Hz CAT = a 2 – 5,002 gon = 80,103 gona
2 = Hz BAT = 85,105 gonb
1 = Hz ACT = 90,759 gonb
2 = Hz ABT = 85,536 gong
1 = 200gon - a 1 - b 1 = 29,138 gong
2 = 200gon - a 2 - b 2 = 29,359 gon![]()
![]()
![]()
![]()
4.4.3. Turmeinzelhöhen
HTo = HA + si * cot Pi,To
HTu = HA + si * cot Pi,Tu
Vom Punkt A aus (si = b1,b2):
HTo1 = 147,255 m
HTu1 = 99,598 m => h1 = 47,657 m
HTo2 = 147,261 m
HTu2 = 99,598 m => h2 = 47,663 m
Vom Punkt B aus (si = a2):
HTo3 = 149,515 m
HTu3 = 101,849 m => h3 = 47,666 m
Vom Punkt C aus (si = a1):
HTo4 = 149,792 m
HTu4 = 102,115 m => h4 = 47,667 m
h = ¼ * (h1 + h2 + h3 + h4) = 47,666 m
Höhe des Turms: H = h + 3,00m = 50,666 m
4.5. Statistik
4.5.1 Standardabweichung einer Einzelhöhe und des arithmetischen Mittels
v = Abweichung vom arithmetischen Mittel
h = 47,666 m
|
Einzelhöhen [m] |
v [mm] |
v2 [mm2] |
|
47,657 |
9 |
81 |
|
47,663 |
3 |
9 |
|
47,666 |
0 |
0 |
|
47,677 |
-11 |
121 |
|
|
å -1 |
å 211 |
![]()
![]()
4.5.2. Standardabweichung des Nivellements:
v = Satzmittel – Meßwert
|
h [m] |
v [mm] |
v² [mm²] |
|
0,48 |
5 |
25 |
|
0,481 |
5 |
25 |
|
|
|
å 50 |
n = 2
![]()
![]()
4.5.3. Horizintalwinkelmessung
Standardabweichung aus Doppelbeobachtungen
|
Satzmittel [gon] |
|
d [mgon] |
d² [mgon²] |
|
4,997 |
5,006 |
-9 |
81 |
|
85,104 |
85,106 |
-2 |
4 |
|
85,536 |
85,536 |
0 |
0 |
|
90,759 |
90,759 |
0 |
0 |
|
|
|
|
å 85 |
n = 4
![]()
![]()
4.5.4. Vertikalwinkelmessung
Standardabweichung aus Doppelbeobachtungen
|
Satzmittel [gon] |
|
d [mgon] |
d² [mgon²] |
|
104,064 |
104,064 |
0 |
0 |
|
104,510 |
104,508 |
2 |
4 |
|
102,735 |
102,728 |
7 |
49 |
|
66,892 |
66,885 |
7 |
49 |
|
100,885 |
100,883 |
2 |
4 |
|
65,466 |
65,464 |
2 |
4 |
|
95,967 |
95,968 |
-1 |
1 |
|
100,691 |
100,689 |
2 |
4 |
|
64,227 |
64,227 |
0 |
0 |
|
95,418 |
95,418 |
0 |
0 |
|
|
|
|
å 115 |
n = 10
![]()
![]()
4.5.5. Standardabweichung der Strecken
AB = 35,431 m
![]()
AC = 34,656 m
![]()
4.5.6. Standardabweichung einer Einzelhöhe nach dem Varianzfortpflanzungsgesetz
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4.6. Abschließende beurteilende Stellungnahme
Um eine noch höhere Meßgenauigkeit zu erreichen, sollten die Winkel
ai und bi eigentlich in etwa 50 gon betragen sowie die Strecken ci in ihrer Länge mit der Höhe des Turmes in etwa übereinstimmen.Dies war aber aufgrund des unwegsamen Geländes sowie der zahlreichen Sträucher und Bäume, die die Sicht von unseren "Wunschpunkten" auf den Turm verdeckten, nicht möglich, so dass die Strecke ci in etwa nur 2/3 der Länge des Turmes aufweisen konnten. Auch die Winkel waren alle mit etwa 85 gon viel zu groß. Zudem kam noch die schlechte Witterung, unter der ein negativer Einfluss auf die Entfernungsmessung des Tachymeter möglich ist.
Trotzdem kann die Gruppe mit ihren Meßergebnissen zufrieden sein, zumal die Standardabweichung der Turmhöhen gerade 8,39 mm beträgt.