Häufigkeitsmaße für Korpora

Jede korpuslinguistische Recherche, die eine quantitative Auswertung von Korpussuchen vornimmt, beginnt mit dem Bestimmen der Häufigkeiten der Suchergebnisse (egal ob das einzelne Worttypes oder komplexere Ausdrücke sind). Diese Häufigkeiten heißen die Korpushäufigkeit oder Gebrauchshäufigkeit, oder auch die Korpusfrequenz oder Gebrauchsfrequenz oder einfach die Häufigkeit oder die Frequenz des Wortes bzw. Ausdrucks.

Es folgt eine Auswahl verschiedener Häufigkeitsmaße, die die Suchergebnisse quantitativ unterschiedlich darstellen und beleuchten. Die zwei geläufigsten Maße sind die absolute und die relative Häufigkeit.

Absolute Häufigkeit

Die absolute Häufigkeit ist die Anzahl der Treffer, d.h. der Vorkommen des gesuchten Wortes oder Ausdrucks im Korpus. Dieses ist das einfachste Häufigkeitsmaß und wird bei der Erstellung von Häufigkeitsverteilungen innerhalb eines einzigen Korpus verwendet (wie später ausführlich gezeigt wird), ist aber nicht nützlich für den Vergleich von Häufigkeiten zwischen Korpora unterschiedlicher Größe.

• In DWDS wird bei der Anzeige der Suchergebnisse die absolute Häufigkeit immer mit angezeigt.
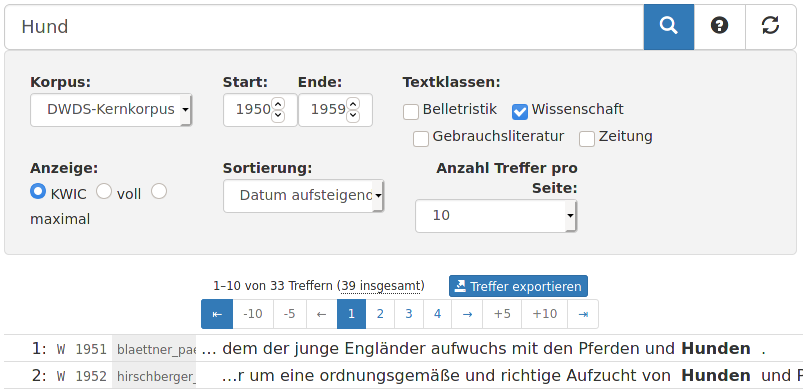
  • In einigen Korpora, insbesondere im Kernkorpus und im Kernkorpus 21, werden sowohl die Anzahl der anzeigbaren Treffer als auch die Anzahl der Treffer insgesamt angezeigt (manche Treffer können aus urheberrechtlichen Gründen nicht angezeigt werden). Nur die Anzahl der Treffer insgesamt sollte man bei einer statistischen Auswertung verwenden – allerdings muss man sich dann darauf verlassen, dass es unter den nicht angezeigten Treffern keine falschen Treffer gibt, was insbesondere bei komplexen Anfragen problematisch sein kann.
• Beispiel: Absolute Häufigkeit des Lemmas ‚Hund‘ im Kernkorpus (7279, wovon 5125 anzeigbar sind):

  

  N.B.: Wenn man den Suchbereich verkleinert, indem man das Start- oder Endjahr ändert oder nicht alle Textklassen auswählt, ändert sich dementsprechend die Anzeige der absoluten Häufigkeit: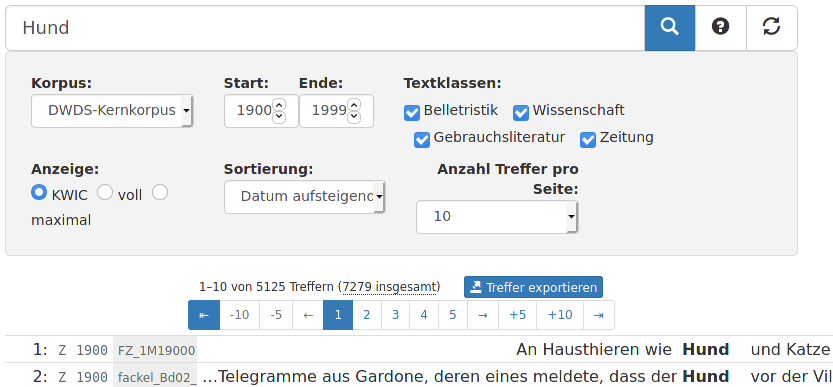
  

  

Relative Häufigkeit

Die relative Häufigkeit ist die Normierung der absoluten Häufigkeit bezüglich der Korpusgröße, indem Ersteres durch Letzteres geteilt wird; formaler ausgedrückt:

• N sei die Anzahl aller Tokens im Korpus, f_a die absolute Häufigkeit des Suchausdrucks.
  Dann ist die relative Häufigkeit f_r = f_a / N.

Damit eignet sich dieses Maß, um die Häufigkeiten der gleichen Einheiten (z.B. Wörter oder komplexerer Ausdrücke) zwischen verschiedenen Korpora (oder verschiedenen Teilen eines Korpus), die nicht gleich groß sind, zu vergleichen und daraus weitere statistische Schlussfolgerungen zu ziehen (womit wir uns später ausführlich beschäftigen werden).

• Eine alternative Darstellung der relativen Häufigkeit ist als Prozent: f_% = f_r × 100.
• In großen Korpora sind relative Häufigkeiten der meisten Wortformen sehr kleine Zahlen, so dass die Darstellung als Dezimalzahl oder Prozent nicht leicht interpretierbar ist. Daher ist die übliche Darstellung in großen Korpora in Instanzen pro Million Wörter: f_pMW = f_r × 1.000.000, abgekürzt pMW (man verwendet diesen Kürzel auch, wenn die Normierungseinheit das Token ist).

In DWDS kann man relative Häufigkeiten anhand der obigen Formeln berechnen. Dafür benötigt man die Korpusgröße, also die Anzahl aller Tokens im Korpus; diese befinden sich für alle DWDS-Korpora auf dieser Seite (unter „Übersicht über die Korpora im DWDS“). (Achtung: Wenn Sie die Zahlen auf dieser Seite per Copy-&-Paste in ein Programm (z.B. R) eingeben, müssen Sie die Leerzeichen manuell entfernen, also nicht ‚121 397 601‘ sondern ‚121397601‘ eingeben.)

• Beispiel: Relative Häufigkeit des Lemmas ‚Hund‘ im DWDS-Kernkorpus
  • Dezimal: 7279 / 121397601 = 0,00005996
  • Prozent: (7279 / 121397601) × 100 = 0,005996%
  • pMW: (7279 / 121397601) × 1000000 = 59,96 pMW

Die Trefferanzeige in DWDS enthält die keine Angabe von relativen – im Gegensatz zu absoluten – Häufigkeiten. Allerdings zeigt das Werkzeug für Wortverlaufskurven zwar relative Häufigkeiten in pMW, jedoch nicht für einzelne Korpora sondern nur für die zusammengefassten Suchergebnisse aus den Referenz- bzw. Zeitungskorpora (dafür aber sowohl insgesamt als auch nach Textklasse).

Für die folgenden Häufigkeitsmaße stellt das DWDS-Abfragesystem keine Anzeigen oder Werkzeuge zur Verfügung.

Proportionale Häufigkeit

Die proportionale Häufigkeit ist die Normierung der absoluten Häufigkeit eines Suchausdrucks bezüglich der Summe der absoluten Häufigkeiten einschlägig verwandter Suchausdrücke. Damit eignet sich dieses Maß, um z.B. die Verhältnisse der Häufigkeiten verschiedener Varianten eines Lemmas zwischen verschiedenen Korpora zu vergleichen. Hier ist eine formale Definition:

• f_a1, f_a2, …, f_aN seien die absoluten Häufigkeiten von N Varianten eines Ausdrucks.
  Dann ist die proportionale Häufigkeit f_p1 = f_a1 / (f_a1 + f_a2 + … + f_aN),
  die proportionale Häufigkeit f_p2 = f_a2 / (f_a1 + f_a2 + … + f_aN),
  …
  die proportionale Häufigkeit f_pN = f_aN / (f_a1 + f_a2 + … + f_aN)

Da in typischen Verwendungen dieses Maßes die Zahlen nicht sehr weit auseinander liegen, ist die Darstellung als Prozent am sinnvollsten, also f_p1 × 100 usw.

• Beispiel: Es gibt zwei Varianten des Partizips II des Verbs senden im Deutschen, die im DWDS-Kernkorpus mit folgenden absoluten Häufigkeiten auftreten: 181 (gesendet) und 736 (gesandt). Die proportionalen Häufigkeiten dieser Varianten im Kernkorpus sind also folgende:
  • gesendet: [181 / (181 + 736)] × 100 = 19,74 ≈ 20%
  • gesandt:   [736 / (181 + 736)] × 100 = 80,26 ≈ 80%

N.B.: Der Begriff „proportionale Häufigkeit“ ist kein gebräuchlicher Begriff in der Korpuslinguistik oder der Statistik: Es handelt sich formal um eine Variante der relativen Häufigkeit, bei der die Bezugsgröße nicht das ganze Korpus sondern nur die Vorkommen der zu vergleichenden Suchbegriffe darstellen. Aber aufgrund dieses Unterschieds ist es im Rahmen einer Darstellung von Korpushäufigkeitsmaßen sinnvoll, auch unterschiedliche Begriffe zu verwenden.

Differenzenkoeffizient

Dieses Häufigkeitsmaß gibt Auskunft darüber, ob die Anzahl der Treffer bei einer Suche in einem Teilkorpus so groß wie erwartet oder größer oder kleiner als erwartet ist (in Bezug auf das Gesamtkorpus). Es wird in der COSMAS II Online-Hilfe wie folgt beschrieben: Der Differenzenkoeffizient „normiert die jeweilige (absolute) Trefferhäufigkeit auf den Bereich -1 bis +1, indem er die tatsächlich auftretende mit der erwarteten Häufigkeit des zugehörigen Korpusquerschnitts vergleicht:

• Ein Wert von annähernd 0 bedeutet, dass der Treffer wie statistisch erwartet auftritt.
• Je mehr der Wert gegen -1 sinkt, desto seltener als erwartet tritt der Treffer auf.
• Je mehr der Wert gegen +1 steigt, desto häufiger als erwartet tritt der Treffer auf.“

Hier ist eine formale Definition des Differenzenkoeffizienten:

• K sei ein Korpus der Größe N Tokens, K_i ein Teilkorpus von K der Größe N_i Tokens, f_a die absolute Häufigkeit eines Wortes W in K, f_b die absolute Häufigkeit (die „beobachtete Frequenz“) von W in K_i, und f_e = (f_a / N) × N_i die erwartete Frequenz von W in K_i.
  Dann ist der Differenzenkoeffizient D = (f_b − f_e) / (f_b + f_e).

Die erwartete Häufigkeit des Ausdrucks im Teilkorpus stellt also das Verhältnis der Teilkorpusgröße zur relativen Häufigkeit des Ausdrucks im Gesamtkorpus dar. Um diese Formel auf Suchergebnisse in DWDS anzuwenden, muss man wie folgt vorgehen:

• Erstens bestimmt man ein Teilkorpus in der Eingabemaske, indem man die Suche auf eine festgelegte Spanne von Start- und Endjahren und / oder (bei den Referenzkorpora) auf eine ausgewählte Textklasse beschränkt (wie z.B. im obigen Screenshot).
• Zweitens braucht man nicht nur die Größe des ganzen Korpus sondern auch des definierten Teilkorpus: in DWDS lassen sich Teilkorpusgrößen nach Dekaden und Textklassen (und auch nach POS (d.h. STTS-Tag), was weniger nützlich ist) auf dieser Seite abfragen, indem man die gewünschten Einstellungen wählt und dann den Button ‚Statistik abfragen‘ anklickt.
• Beispiel: Differenzenkoeffizient des Lemmas ‚Hund‘ aus der Dekade 1960-1969 im DWDS-Kernkorpus
  • Beobachtete (absolute) Häufigkeit f_b in der ausgewählten Dekade: 474
  • Teilkorpusgröße N_i: 10587420 (ermittelt wie oben beschrieben und hier angezeigt)
  • Erwartete Häufigkeit f_e in der ausgewählten Dekade: 7279 / 121397601 × 10587420 = 635 (aufgerundet)
  • Differenzenkoeffizient: (474 − 635) / (474 + 635) = −0,145
    Nach diesem Ergebnis tritt das Lemma ‚Hund‘ in dieser Dekade etwas seltener als erwartet (in Bezug auf das ganze Korpus) auf.

Häufigkeitsklasse

Dieses Häufigkeitsmaß gibt den Klassen- oder Gruppenrang eines Types oder Lemmas im Vergleich zur Klasse des häufigsten Types oder Lemmas im Korpus an. Es wird in der COSMAS II Online-Hilfe wie folgt beschrieben: „Die Treffer werden durch Vergleich ihrer Häufigkeit mit der des häufigsten Wortes der deutschen Sprache "der" auf Häufigkeitsklassen abgebildet. Das häufigste Wort hat die Klasse 0. Treffer in der Häufigkeitsklasse 1, 2, etc. treten annähernd ½ ¼, etc. mal so oft wie das häufigste Wort auf. Mit jeder höheren Klasse N verringert sich die Trefferhäufigkeit auf 1/2^N.“

Hier ist eine formale Definition (nach Perkuhn et al. S.80):

• f_a(W) sei die absolute Häufigkeit des Wortes W im gegebenen Korpus, f_a(R) die absolute Häufigkeit des häufigsten Wortes im Korpus (des Referenzwortes). Dann ist die Häufigkeitsklasse von W, K_W = [log₂(f_a(R) / f_a(W))].
  ([x] steht für die ganze Zahl, die x am nächsten ist, z.B. [2,3] = 2 und [2,7] = 3.)

In dieser Formel berechnet log₂ den Logarithmus zur Basis 2, ergibt also, wie oft 2 mit sich selbst multipliziert (potenziert) wird, z.B. gilt log2(8) = 3 und log2(16) = 4, weil 2³ = 8 und 2⁴ = 16. Da die Berechnung der Häufigkeitsklasse das Verhältnis der Häufigkeit des Referenzwortes f_a(R) zur Häufigkeit eines anderen Wortes f_a(W) (die definitionsgemäß nicht größer sein kann als f_a(R)) beinhaltet, bedeutet das die Halbierung der Trefferhäufigkeit bei jeder Erhöhung der Klasse, und weil log₂(f_a(R) / f_a(R)) = log2(1) = 0, ist die Häufigkeitsklasse 0 die Klasse des Referenzwortes.

• Beispiel: Häufigkeitsklasse des Lemmas ‚Hund‘ im DWDS-Kernkorpus
  • Absolute Häufigkeit des Lemmas des Referenzworts ‚der‘: 11113606
  • log₂(11113606 / 7279) = 10,58
  • Häufigkeitsklasse: 11

Mit Hilfe der obigen Formel kann man auch eine Tabelle aller Häufigkeitsklassen eines Korpus erstellen, die für jede Klasse die Spanne (also den minimalen und maximalen Wert) der absoluten Häufigkeiten angibt:

• Klasse	Minimal	Maximal
  0	7858507	11113606
  1	3929254	7858506
  2	1964627	3929253
  3	982314	1964626
  4	491157	982313
  5	245579	491156
  6	122790	245578
  7	61395	122789

  Klasse	Minimal	Maximal
  8	30698	61394
  9	15349	30697
  10	7675	15348
  11	3838	7674
  12	1919	3837
  13	960	1918
  14	480	959
  15	240	479

  Klasse	Minimal	Maximal
  16	120	239
  17	60	119
  18	30	59
  19	15	29
  20	8	14
  21	4	7
  22	2	3
  23	1	1

Durch diese Tabelle gewinnt man einen ersten Eindruck über die Verteilung der Häufigkeiten im Korpus und damit über die numerische Gestalt des Korpus. (Wir werden sehen, wie man solche Tabellen mit R erstellen kann.)

In Perkuhn et al. wird auf folgende Eigenschaften von Häufigkeitsklassen hingewiesen:

• „In jedem beliebigen Korpus umfasst die höchste vertretene Häufigkeitsklasse ausschließlich die Worttypes mit der absoluten Frequenz 1. Solche Wörter mit genau einem Vorkommen im Korpus nennt man Hapax legomena“ (kurz: Hapaxe) (Perkuhn et al., S. 81).
• Zwischen zwei benachbarten Häufigkeitsklassen kann das Häufigkeitsverhältnis im Extremfall bei fast 1:1 (mit einem Häufigkeitsunterschied von einem Vorkommen) an benachbarten Rändern bzw. bei fast 4:1 an entgegengesetzten Rändern liegen (ebd.).
• Häufigkeitsklassen geben nicht so genaue Auskunft über Korpushäufigkeiten wie die relative Häufigkeit einzelner Wörter, dafür sind sie robuster als dieser: „Verkleinert man das Korpus durch Zufallsauswahl von Texten z.B. auf die Hälfte oder auf ein Zehntel, dann bleibt die Häufigkeitsklasse i.A. weitgehend unverändert“ (Perkuhn et al., S. 82). Aber mindestens zehn Vorkommen eines Wortes sind für die statistische Zuverlässigkeit von Häufigkeitsklassen erforderlich (S. 90).

In diesem Seminar werden wir die vorgestellten Häufigkeitsmaßen, wie auch alle anderen quantitativen Korpusauswertungen von Suchergebnissen in DWDS, mit dem Softwarepaket R ermitteln. Daher geben wir als nächstes eine kurze Einführung in den Umgang mit R.