IWRM Unstrut, Germany
Problem description
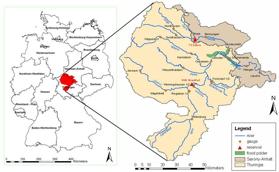 The River Unstrut catchment with an area of 6343 km2 in Thuringia and Saxony-Anhalt, Germany, is highly prone to
flooding and the region suffered from severe damage during both historical and recent flood events. The
present flood retention system consists of two dams, a flood channel and four polders. In order to cope with
future floods, the flood retention system is to be extended and an number of technical measures are proposed & their
effects modelled. How can we find out which measure is the best, given the local hydrologic/hydraulic and
socio-geographical circumstances? At first, it seems evident... the one that reduces damages the most.
But, ...
The River Unstrut catchment with an area of 6343 km2 in Thuringia and Saxony-Anhalt, Germany, is highly prone to
flooding and the region suffered from severe damage during both historical and recent flood events. The
present flood retention system consists of two dams, a flood channel and four polders. In order to cope with
future floods, the flood retention system is to be extended and an number of technical measures are proposed & their
effects modelled. How can we find out which measure is the best, given the local hydrologic/hydraulic and
socio-geographical circumstances? At first, it seems evident... the one that reduces damages the most.
But, ...
- if 'damage' is only expressed in monetary units, high-value industries will primarily be saved
- retention structures will have a different effect on flood waves with different hydrographs, so... which hydrograph should we select?
Multiple Criteria Decision Making
The first 'but' can be avoided by increasing the number of criteria. If criteria like vulnerable institutions (schools, hospitals, ...), the occurence of life threathening situations (defined by water depth, flow velocity and water level rise), number of affecter people, etc. are included in the decision making process. Weights can be attributed to these criteria in order to differentiate their importance. The second 'but' is not so easily solved...
Multivariate Plausibilities
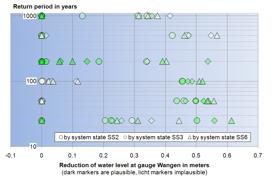 Classically, return periods are defined by their flood peak. So, we could define the structure's performance in
decrease in damages per return period. Since not only the flood peak, but also the flood volume is responsible for
flood damages, a second probability complicates the problem. Or should we classify the effect accordig to a joint probability?
Now, we have also found that for certain flood peak and/or flood volume return periods, flood
retention structures might actually increase the flood impact! How can we combine this multitude of data?
Classically, return periods are defined by their flood peak. So, we could define the structure's performance in
decrease in damages per return period. Since not only the flood peak, but also the flood volume is responsible for
flood damages, a second probability complicates the problem. Or should we classify the effect accordig to a joint probability?
Now, we have also found that for certain flood peak and/or flood volume return periods, flood
retention structures might actually increase the flood impact! How can we combine this multitude of data?
Fuzzy Logic and Decision Support
We have developed a methodology that retains the 'classical' risk-based procedure of analysing different flood peaks and combining them to a decision. We integrate the flood volume probability using fuzzy logic into the classical return period. This way, we have turned the 'crisp' probability into a -more realistic- inprecise probability. This has the advantage that the decision makers can use familiar procedures and algorithms with these inprecise probabilities. A second advantage is that the inherent uncertainty on which a decicion maker has to base his decision is not hidden but can displayed graphically. It is better to make an accurate decision based on inprecise data than to make an inprecise decision on so-called accurate data.