↑ Sitemap

Drei wichtige Wahrscheinlichkeitsverteilungen

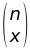
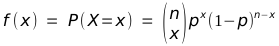
Im Folgenden werden drei häufig verwendete Wahrscheinlichkeitsverteilungen vorgestellt. Dabei handelt es sich eigentlich um drei Familien von Wahrscheinlichkeitsverteilungen, deren wesentlichen Eigenschaften durch die jeweils dazugehörigen Wahrscheinlichkeits(dichte)funktionen bestimmt sind. Die spezifischen Verteilungen innerhalb einer Familie unterscheiden sich in einem oder mehr Parameter (Argumente) dieser Funktionen, die man deswegen auch als Parameter der entsprechenden Verteilungen bezeichnet.

Die Binomialverteilung

Binomialverteilungen sind diskrete Wahrscheinlichkeitsverteilungen; sie ergeben sich aus Zufallsexperimenten, die folgende Eigenschaften haben:

Das Experiment besteht aus n identischen und unabhängigen Stufen (d.h. Wiederholungen oder Versuchen).
In jeder Stufe gibt es zwei mögliche sich ausschließende Ergebnisse, die konventionell „Erfolg“ und „Misserfolg“ heißen.
In jeder Stufe ist die Wahrscheinlichkeit des Erfolgs eine feste Zahl p und folglich die Wahrscheinlichkeit des Misserfolgs die Zahl 1 − p; Erfolg und Misserfolg sind also Gegenereignisse voneinander und das Verhältnis bleibt über alle Stufen des Experiments hinweg erhalten.
Demnach gilt: Ist die Anzahl der Erfolge in einem solchen Zufallsexperiment aus n Stufen = x, dann ist die Anzahl der Misserfolge = n − x.

Das Standardbeispiel einer Binomialverteilung ist die Anzahl der Köpfe (oder der Zahlen) bei einer Reihe von Münzwürfen. Aber in vielen Arten von statistischer Untersuchung, wo man zwischen „Erfolg“ und „Misserfolg“ unterscheidet, kann die Binomialverteilung nützlich sein, z.B. bei der Wirksamkeit von Medikamenten aber auch beim Auftreten von Wörtern oder syntaktischen Konstruktionen in einem Korpus (wie wir später im Detail sehen werden).

Exkurs: Wahrscheinlichkeitsfunktion

Es mag von Interesse sein zu sehen, wie sich die Formel der Wahrscheinlichkeitsfunktion der Binomialverteilung mit x Erfolgen und n − x Misserfolgen aus den oben aufgelisteten Eigenschaften ergibt:

Da die Stufen des Experiments unabhängig voneinander sind, ist (gemäß der Multiplikationsregel) die Wahrscheinlichkeit einer beliebigen Kombination von x Erfolgen und n − x Misserfolgen gleich dem Produkt der Wahrscheinlichkeiten der Erfolge und der Misserfolge: p × p × … (x-mal) × 1−p × 1−p × … (n−x-mal) = px(1 − p)n − x.
Für die Berechnung der Wahrscheinlichkeit über alle n Stufen des Zufallsexperiments muss die Gesamtzahl aller Kombinationen von x Erfolgen und n − x Misserfolgen berücksichtigt werden; man kann zeigen, dass diese Zahl gleich dem folgenden Quotienten ist (wo die Fakultät m! = m × (m − 1) × (m − 2) × … × 1):

n!
x!(n − x)! , der meist in Form des sogenannten Binomialkoeffizienten angegeben wird: .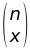
Schließlich, da immer nur eine einzige Kombination von x Erfolgen und n − x Misserfolgen in einer Stufe des Zufallsexperiments auftreten kann, folgt daraus, dass die Wahrscheinlichkeit über alle Stufen des Experiments gleich der Summe der Wahrscheinlichkeiten der einzelnen Kombinationen ist, und diese Summe wiederum (da jede Kombination die Wahrscheinlichkeit px(1 − p)n − x hat) ist gleich dem Produkt der Wahrscheinlichkeit einer Kombination und der Gesamtzahl aller Kombinationen. Dieses Produkt ist die Definition der Wahrscheinlichkeitsfunktion f(x) der Binomialverteilung:

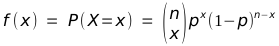
Die Verteilungsfunktion F(x) der Binomialverteilung ergibt sich aus einer Summe dieser Wahrscheinlichkeiten:

In dieser Formel lässt sich übrigens der Namensgeber der Binomialverteilung erkennen, der binomische Lehrsatz:

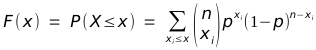
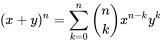
Die Zahlen n (Anzahl der Stufen des Zufallsexperiments) und p (Wahrscheinlichkeit des Erfolgs) sind die Parameter der Binomialverteilung. Bei der Angabe einer binomialverteilten Zufallsvariable sollten diese Parameter immer mit angegeben werden; eine geläufige Schreibweise ist die folgende:

X∼B(n, p)

Beispielsweise ist X∼B(100, 0.15) die binomialverteilte Zufallsvariable für ein Zufallsexperiment mit 100 Stufen und Wahrscheinlichkeit des Erfolgs von 15%.

Der Erwartungswert (das arithmetische Mittel) einer binomialverteilten Zufallsvariable X∼B(n, p) = np und die Varianz = np(1 − p) (und die Standardabweichung dementsprechend = √np(1−p) ). Diese Formeln lassen sich wie folgt ableiten:

Für jede Stufe eines n-stufigen Zufallsexperiments kann man eine Zufallsvariable Xi (i = 1, …, n) definieren, mit Xi = 1 bei Erfolg und Xi = 0 bei Misserfolg (die Xi sind sogenannte Bernoulli-verteilte Zufallsvariablen). Dann ist die Zufallsvariable X des ganzen Zufallsexperiments = X1 + … + Xn.
Da P(Xi = 1) = p und P(Xi = 0) = 1 − p, gilt:
der Erwartungswert E(Xi) = Σxi f(xi) = 1 × p + 0 × (1 − p) = p und
die Varianz Var(Xi) = E(Xi2) − (E(Xi))2 = p − p2 = p(1 − p).
Man kann beweisen, dass E(X1 + … + Xn) = E(X1) + … + E(Xn) und Var(X1 + … + Xn) = Var(X1) + … + Var(Xn).
Somit gilt:
E(X) = p + … + p (n Mal) = np und
Var(X) = p(1 − p) + … + p(1 − p) (n Mal) = np(1 − p).

Grafische Darstellungen

Hier sind grafische Darstellungen von vier verschiedenen Binomialverteilungen:

In jeder Grafik stellen die x-Achse die Anzahl der Stufen des Zufallsexperiments und die y-Achse die Wahrscheinlichkeit des Erfolgs dar.
In den ersten zwei Grafiken bedeuten die Punkte bei 6-50 bzw. 11-50 Stufen, dass die Wahrscheinlichkeit des Erfolgs in diesen Anzahlen von Stufen tatsächlich Null ist, weil es diese Stufen im jeweiligen Zufallsexperiment ja gar nicht gibt.
Dagegen hat in den Grafiken der 50-stufigen Zufallsexperimente jede der 50 Stufen eine Wahrscheinlichkeit des Erfolgs größer als Null, auch wenn in ca. 60% der Stufen diese Wahrscheinlichkeit nur sehr knapp über Null liegt.
In jeder Grafik ist der Erwartungswert (das arithmetische Mittel) der Erfolge np gut erkennbar; dem entspricht in jeder Verteilung der Modalwert und in den ersten drei auch der Median, weil es sich hier mit p = 0,5 um symmetrische Verteilungen handelt, während bei der letzten mit p = 0,33 leicht asymmetrischen Verteilung der Median knapp unter dem Erwartungswert liegt.
Die Gestalt der Verteilungen hängt von der Kombination der Parameterwerte ab: Bei der Wahrscheinlichkeit 50% sind die Verteilungen in jedem Fall symmetrisch, aber auch bei p = 33% ist die Verteilung eines 50-stufigen Zufallsexperiments symmetrisch für Wahrscheinlichkeiten, die nicht fast gleich Null sind. Aber mit derselben Stufigkeit bei sehr hoher oder sehr niedriger Wahrscheinlichkeit des Erfolgs sind die Verteilungen ziemlich schief:

Jedoch bei einer hohen Stufigkeit sind die Verteilungen auch bei sehr hoher oder sehr niedriger Wahrscheinlichkeit des Erfolgs wieder symmetrisch (für Wahrscheinlichkeiten, die nicht fast gleich Null sind):

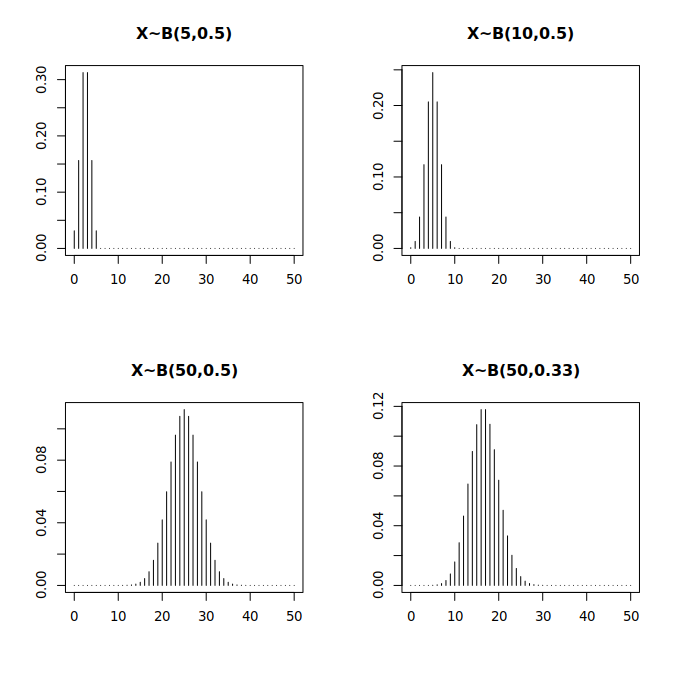
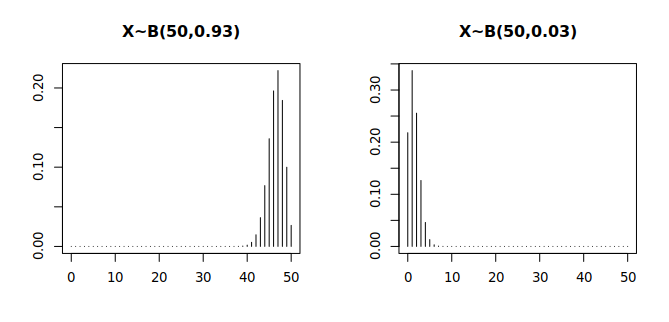
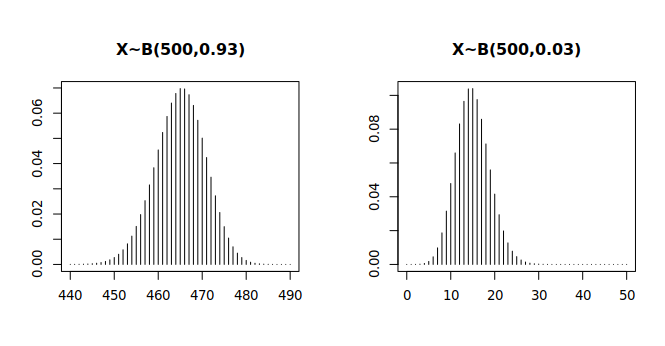
Abschließend weisen wir darauf hin, dass das sogenannte Galtonbrett eine sehr anschauliche (und in Videos mitunter auch unterhaltsame) empirische Demonstration des Zustandekommens der Binomialverteilung zeigt (bzw. als Annäherung dazu der Normalverteilung, der wir uns jetzt zuwenden).

Die Normalverteilung

Die Normalverteilung ist eine stetige Version von symmetrischen Binomialverteilungen. Ihre Entwicklung geht auf den Versuch zurück, eine rechnerisch handhabbare Abschätzung der Bionomialkoeffizienten zu finden, denn die darin vorkommenden Fakultäten sind außer bei kleinen Zahlen sehr rechenintensiv (selbst für moderne Computer). Die seinerzeit (ca. 1730) endeckte Abschätzung heißt die Stirlingformel: n! ≈ nne−n√2πn (vgl. die Wahrscheinlichkeitsdichte der Normalverteilung gleich unten).

Viele natürlich vorkommende Phänomene weisen annähernd eine Normalverteilung auf (z.B. die Verteilung der menschlichen Korpergröße). Darüber hinaus gibt es einen Satz der Wahrscheinlichkeitstheorie, den zentralen Grenzwertsatz, der zeigt, dass sich die Verteilungen der Mittelwerte von Stichproben bei zunehmender Größe (bzw. zunehmender Anzahl von Stichproben) einer Normalverteilung nähern, auch wenn die Verteilungen der Stichproben selbst nicht normalverteilt sind. Aus diesem Grund spielt die Normalverteilung eine wichtige Rolle in vielen statistischen Verfahren.

Die Normalverteilung ist eine Familie stetiger Wahrscheinlichkeitsverteilungen mit den Parametern μ (dem Erwartungswert der Verteilung) und σ (der Standardabweichung der Verteilung; manche Autoren verwenden die Varianz σ2 als den zweiten Parameter). Eine normalverteilte Zufallsvariable X∼N(μ, σ) hat folgende Wahrscheinlichkeitsdichte f(x) (π ist die Kreiszahl ≈ 3,14159 und e die Eulersche Zahl ≈ 2,71828):

Die Graphen dieser Funktion, für gegebene Werte von μ und σ, sind symmetrische Kurven, bei denen also das arithmetische Mittel, der Median und der Modalwert alle = μ sind und das Abbild dieses Werts der höchste Punkt am Graphen der Wahrscheinlichkeitsdichte ist, d.h. f(μ) = 1/[σ√2π] (denn wenn x = μ, ist der Exponent von e = 0 und e0 = 1; dementsprechend ist für alle anderen Werte von x der Wert von f(x) kleiner). Insbesondere hat der Graph der normalverteilten Zufallsvariable Z∼N(0, 1), der sogenannten Standardnormalverteilung (der Buchstabe Z statt X ist hierfür üblich), in der typischen Darstellung (wo die x- und y-Achsen unterschiedlich skaliert sind) eine glockenähnliche Gestalt und ist deswegen auch als (Gaußsche, nach dem Mathematiker Gauß) Glockenkurve bekannt.

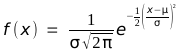
Die folgenden Grafiken zeigen die wesentlichen Eigenschaften der Normalverteilung und verschiedene Normalverteilungen, die sich in den Werten ihrer Parameter unterscheiden:

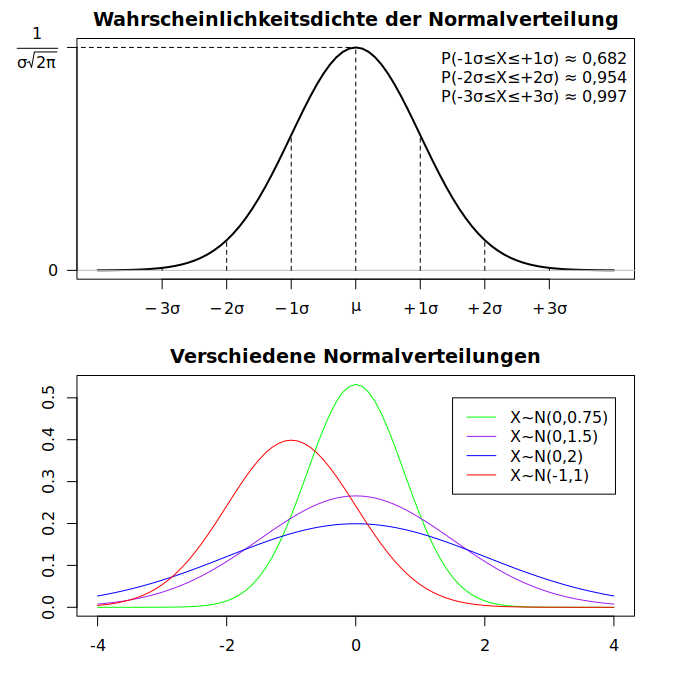
Bei jeder dieser Kurven ist der Prozentanteil der Fläche zwischen der Kurve und der x-Achse, die von sukzessiven Standardabweichungen unterhalb und oberhalb des arithmetischen Mittels bestimmt wird, immer derselbe: Plus/minus eine Standardabweichung beinhaltet ca. 68,2% der Gesamtfläche, plus/minus zwei Standardabweichungen beinhalten ca. 95,4% und plus/minus drei Standardabweichungen ca. 99,7% der Gesamtfläche. Da die Fläche unterhalb der Kurve dem gesamten Wahrscheinlichkeitsmaß entspricht, folgt daraus, dass es sehr unwahrscheinlich ist (ca. 0,03%), dass eine normalverteilte Zufallsvariable Werte hat, die weiter weg als drei Standardabweichungen vom Mittelwert liegen.

Normal-Approximation der Binomialverteilung

Für eine Binomialverteilung X∼B(n, p) kann die Normalverteilung Y∼N(np, √np(1−p) ) – also eine Normalverteilung mit dem Erwartungswert und der Standardabweichung der binomialverteilten Zufallsvariable als Parametern – u.U. eine gute Annäherung sein, wie die folgende Grafik veranschaulicht. Die Voraussetzung für die Güte der Approximation ist, dass n nicht zu klein ist und p weder zu klein (nahe 0) noch zu groß (nahe 1). Diese Approximation ist eine Folge des zentralen Grenzwertsatzes.

Standardisierung

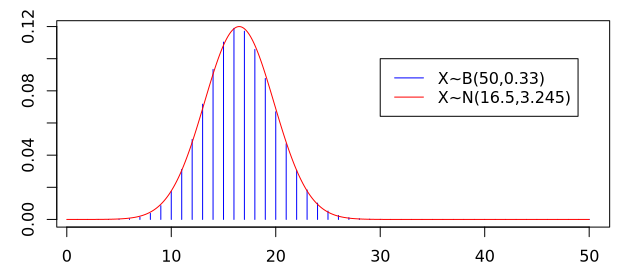
Jede Normalverteilung kann mit Hilfe folgender Formel in die Standardnormalverteilung umgewandelt werden:

z = x − μ
σ

In dieser Formel stehen x für einen Wert aus einer beliebigen Normalverteilung und μ und σ für den Erwartungswert (arithmetischen Mittel) bzw. die Standardabweichung dieser Normalverteilung. Das Ergebnis z ist der entsprechende Wert der Standardnormalverteilung und heißt deswegen ein z-Wert. Wenn man jeden Wert einer Normalverteilung so in einen z-Wert umwandelt, wird aus der Normalverteilung die Standardnormalverteilung. Dieser Umwandlungsprozess heißt Standardisierung oder auch z-Transformation.

Als Beispiel berechnen wir z-Werte für vier Werte aus der obigen Normalverteilung X~N(16.5,3.245), also mit dem Erwartungswert 16,5 und der Standardabweichung 3,245: zuerst für eben diesen Erwartungswert, zweitens für den Wert, der der ersten größeren Standardabweichung entspricht, und schließlich für die Werte 15 und 20. Wenn wir diese Werte für x in die Standardisierungsformel einsetzen, ergeben sich folgende Gleichungen:

16,5 − 16,5
3,245

(16,5 + 3,245) − 16,5
3,245

15 − 16,5
3,245

≈

−0,46

20 − 16,5
3,245

≈

1,08

Die ersten zwei Gleichungen bestätigen einfach die Korrektheit der Standardisierungsformel: der Erwartungswert der Standardnormalverteilung = 0 und die erste (größere bzw. positive) Standardabweichung = 1. Die dritte Gleichung zeigt, dass der Wert 15 in der obigen Normalverteilung einem Wert ungefähr halbwegs zwischen dem Erwartungswert und der ersten kleineren Standardabweichung in der Standardnormalverteilung entspricht, und die vierte Gleichung zeigt, dass der Wert 20 in der obigen Normalverteilung einem Wert entspricht, der knapp größer ist als eine Standardabweichung. Die folgende grafische Darstellung dieser Normalverteilung und der Standardnormalverteilung veranschaulicht diese Ergebnisse:

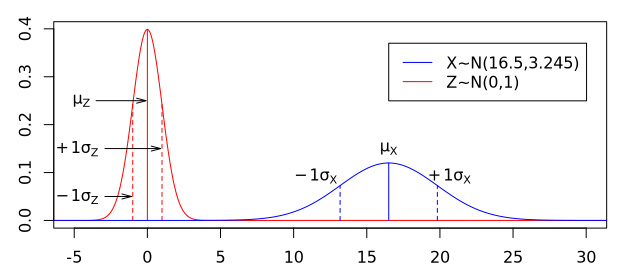
Da beide Verteilungen in derselben Skalierung dargestellt sind, sieht man deutlich die unterschiedlichen Streuungen: Die Standardabweichung der einen Normalverteilung ist über dreimal größer als die der Standardnormalverteilung. Dies führt dazu, dass der Graph Letzterer deutlich schmaler und beim Erwartungswert höher als der Graph Ersterer ist, was eine Folge der Definition von Wahrscheinlichkeit ist, wonach die Fläche unter der Kurve jeder Normalverteilung (vielmehr: unter der Kurve jeder stetigen Wahrscheinlichkeitsverteilung) immer = 1 ist.

Manuelle Berechnungen von Wahrscheinlichkeiten anhand der mathematischen Formel (d.h. der Wahrscheinlichkeitsdichte) der Normalverteilung sind aufwändig, deswegen wurden früher große Tabellen erstellt, in denen man viele ausgewählte Wahrscheinlichkeiten nachschlagen konnte. Diese Tabellen basieren auf der Standardnormalverteilung, enthalten also Wahrscheinlichkeiten nur für z-Werte (oder für Intervalle, die durch z-Werte bestimmt sind). Aber mit Hilfe der Standardisierung kann man solche Tabellen auch für Normalverteilungen mit anderen Parameterwerten nutzen. Wollte man z.B. für die Normalverteilung X~N(16.5,3.245) herausfinden, was die Wahrscheinlichkeit eines Wertes ≥ 20 ist, würde man in der Tabelle beim z-Wert 1,08 nachschauen, weil dieser Wert in der Standardnormalverteilung annähernd dem Wert in der fraglichen Normalverteilung entspricht, wie wir oben gesehen haben (das Ergebnis ist ungefähr 14%). Heutzutage werden solche Tabellen allerdings selten verwendet, denn man kann die Wahrscheinlichkeiten leicht mit Computerprogrammen wie z.B. R berechnen, wie wir sehen werden.

Die Chi-Quadrat-Verteilung

Eine weitere wichtige Familie stetiger Wahrscheinlichkeitsverteilungen ist die Chi-Quadrat-Verteilung, der die Standardnormalverteilung zugrundeliegt.

Die Chi-Quadrat-Verteilung (genannt nach dem griechischen Buchstaben χ und oft so geschrieben: χ2-Verteilung; die entsprechende Zufallsvariable wird meist als X2 geschrieben) ist definiert als eine Summe unabhängiger quadrierter standardnormalverteilter Zufallsvariablen Z_i ∼N(0, 1):

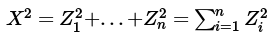
$X^2 = Z_1^2 + ... + Z_n^2 = \sum_{i=1}^n Z_i^2$

Die Anzahl n der standardnormalverteilten Zufallsvariablen ist der einzige Parameter der Chi-Quadrat-Verteilung und heißt die Freiheitsgrade der Verteilung (mehr zu diesem Begriff später). Die Zufallsvariable X2∼χ2(3) hat also eine Chi-Quadrat-Verteilung mit drei Freiheitsgraden. Die Anzahl der Freiheitsgrade bestimmt die Gestalt der Graphen der Wahrscheinlichkeitsdichte der Chi-Quadrat-Verteilung (diese Funktion ist zu komplex, um sie hier zu erläutern):

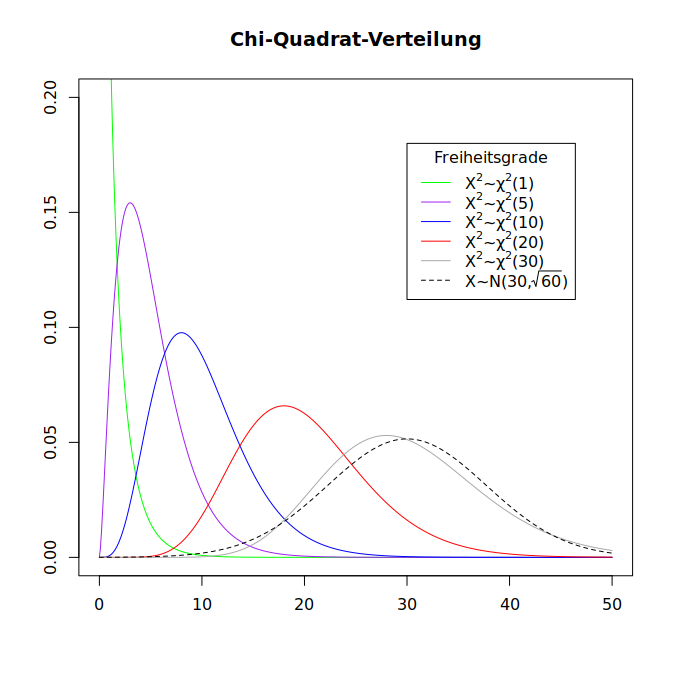
Diese Grafik deutet auf einige der Eigenschaften von Chi-Quadrat-Verteilungen hin:

Alle Werte der Wahrscheinlichkeitsdichte sind positiv (als Folge der Quadrierung).
Der Erwartungswert einer Chi-Quadrat-Verteilung mit n Freiheitsgraden = n; die entsprechende Varianz = 2n.
Bei wenigen Freiheitsgraden ist die Chi-Quadrat-Verteilung stark rechtsschief; die Schiefe verringert sich mit Zunahme der Freiheitsgrade: ab n ≈ 30 Freiheitsgraden ist die Chi-Quadrat-Verteilung der Normalverteilung X∼N(n, √2n) sehr ähnlich.

Die Chi-Quadrat-Verteilung wird bei statistischen Auswertungen in der Korpuslinguistik häufig eingesetzt; verschiedene Beispiele werden wir später sehen.

← Statistik und Wahrscheinlichkeit

↑ Sitemap

Wahrscheinlichkeitsverteilungen mit R →