← Wahrscheinlichkeitsverteilungen ↑ Sitemap Übungsaufgaben →

Wahrscheinlichkeitsverteilungen mit R

Wenn eine Wahrscheinlichkeitsverteilung durch eine mathematische Formel beschrieben werden kann, kann man diese Formel oft direkt in R übersetzen. Nehmen wir als Beispiel die Wahrscheinlichkeitsfunktion der Binomialverteilung und ein Zufallsexperiment bestehend aus 10 Würfen einer fairen Münze, d.h. mit der binomialverteilten Zufallsvariable X ∼ B(10, 0.5). Was ist die Wahrscheinlichkeit von 3 Köpfen bei den 10 Würfen? R hat eine eingebaute Funktion für Fakultäten, factorial(), die die Berechnung von Binomialkoeffizienten erleichtert. Damit können wir mit folgenden Eingaben die Wahrscheinlichkeit berechnen:

Die Wahrscheinlichkeit liegt also bei knapp 12%. Die Berechnung geht aber einfacher, denn R hat auch eine eingebaute Funktion für den Binomialkoeffizienten, choose():

Und es geht sogar noch einfacher, denn R hat eine eingebaute Funktion eigens für die Berechnung von binomialverteilten Wahrscheinlichkeiten, dbinom():

R-Funktionen für Wahrscheinlichkeitsverteilungen

Nicht nur für die Binomialverteilung sondern für viele bekannte Wahrscheinlichkeitsverteilungen gibt es eingebaute R-Funktionen, und zwar jeweils vier: für die Wahrscheinlichkeits(dichte)funktion (die Zähldichte bei diskreten Zufallsvariablen bzw. die Wahrscheinlichkeitsdichte bei stetigen Zufallsvariablen), für die Verteilungs- und die Quantilfunktion, und schließlich für die Simulation von Zufallsexperimenten mit Zufallswerten. Diese R-Funktionen beginnen jeweils mit den Buchstaben ‚d‘, ‚p‘, ‚q‘ bzw. ‚r‘ (für random, also zufällig), und nehmen zum Teil dieselben Argumente, zum Teil unterschiedliche, je nach den Parametern der entsprechenden Wahrscheinlichkeitsverteilungen. Hier ist zusammengefasst eine Beschreibung der R-Funktionen für die drei vorhin vorgestellten Wahrscheinlichkeitsverteilungen:

Es gibt bestimmte Gesetzmäßigkeiten zwischen den d-, p- und q-Funktionen:

Wie oben angemerkt berechnen die Funktionen dnorm(), pnorm() und qnorm() mit den voreingestellten Werten der Argumente mean und sd Werte für die Standardnormalverteilung. Folglich beinhalten diese Funktionen auch die Standardisierung (z-Transformation). Wir haben vorhin am Beispiel der Normalverteilung X~N(16.5,3.245) darauf hingewiesen, dass man durch Standardisierung die Wahrscheinlichkeit eines Wertes ≥ 20 in einer Tabelle von z-Werte nachschlagen kann, und zwar mit dem z-Wert (20 − 16,5)/3,245 ≈ 1,08. In R bekommt man die Wahrscheinlichkeit einfach mit pnorm():

Da der z-Wert 1,08 abgerundet ist, ist auch die berechnete Wahrscheinlichkeit entsprechend ungenau. Ein genaueres Ergebnis erhält man, wenn man auch die Berechnung des z-Werts R überlässt:

Die Werte 16,5 und 3,245 sind aber der Erwartungswert bzw. die Standardabweichung dieser Binomialverteilung, daher können wir diese Werte den entsprechenden Argumenten von pnorm() übergeben, ohne dabei den Wert 20 aus der Verteilung zu standardisieren:

Stichprobenverteilung von Korpushäufigkeiten

Stichprobenverteilungen, denen eine Wahrscheinlichkeitsverteilung zugrundeliegt, für die es in R entsprechende Funktionen gibt, kann man mit Hilfe der passenden d-Funktionen erstellen und auch grafisch darstellen. Ein Standardbeispiel in der Korpuslinguistik ist die Verteilung der Korpushäufigkeit von Wortformen, von denen man annimt, dass sie zwei Bedingungen erfüllt:

Diese Annahmen stellen zugegebenermaßen Vereinfachungen der Wirklichkeit dar, aber solche Vereinfachungen gehören zur üblichen wissenschaftlichen Vorgehensweise beim Versuch, die Wirklichkeit durch mathematische Modelle abzubilden. Die zweite Annahme insbesondere trifft im normalen Sprachgebrauch, wo der Kontext das Auftreten von Wörtern sehr wohl beeinflusst, im Allgemeinen natürlich nicht zu (zumal auf der Satzebene), dennoch: Die „Rechtfertigung für die Binomial-Annahme basiert auf der grundsätzlich plausiblen Vermutung, dass die relevanten Einflüsse auf die Auftretenswahrscheinlichkeit eines Wortes relativ lokal sind (also nicht über große Entfernungen im Korpus wirken) und sich über eine große Zahl von Texten gegenseitig neutralisieren, so dass bei einem sehr großen Korpus die Gesamtfrequenz des Wortes tatsächlich fast ausschließlich von seiner (angenommenen) festen Auftretenswahrscheinlichkeit beeinflusst wird“ (Perkuhn et al., S. 89).

Als Beispiel erstellen wir die Stichprobenverteilung des Wortes Hund im DWDS-Kernkorpus. Zunächst ermitteln wir die absolute Häufigkeit anhand des Suchbegriffs ‚@Hund‘ und die relative Häufigkeit bezüglich der Korpusgröße wie gehabt mit Hilfe der Funktion freq.rel() (die ggf. mit dem source()-Aufruf in R geladen werden muss). Für Berechnungen in R mit diesen Werten sollen sie derselben Größenordnung sein, daher lassen wir die relative Häufigkeit als Dezimalzahl ausgeben (und der Anschaulichkeit wegen auch in pMW):

Für die Erstellung der Verteilung können wir natürlich nicht alle möglichen Stichproben aus der Grundgesamtheit berücksichtigen, aber für unsere Zwecke ist eine Stufigkeit von einer Million eine ausreichende und auch sinnvolle Annäherung, weil wir die relative Häufigkeit normalerweise auch in pMW berechnen. Demnach handelt es sich um die Stichprobenverteilung der binomialverteilten Zufallsvariable X ∼ B(1e6, 3.620335e-05).

Für die grafische Darstellung dieser Verteilung könnten wir im Prinzip alle der einen Million Wahrscheinlichkeiten, die sich aus der gewählten Stufigkeit ergeben, berechnen und grafisch abbilden, aber ganz abgesehen vom Rechenaufwand für den Computer ist es auch gar nicht sinnvoll so viele Werte zu verwenden, denn aufgrund der Wahrscheinlichkeitsfunktion der Binomialverteilung können wir feststellen, dass die allermeisten dieser Wahrscheinlichkeiten verschwindend klein und daher erst recht grafisch vernachlässigbar sind. Mit Hilfe der Funktion qbinom() können wir eine für die grafische Darstellung ausreichende Anzahl der grafisch abzubildenden Wahrscheinlichkeiten bestimmen, indem wir der Funktion eine sehr kleine Wahrscheinlichkeit übergeben, z.B. eine Millionstel (1e-6 in der Exponentialdarstellung):

Diese Ergebnisse bedeuten, dass in einer Stichprobe aus dieser Grundgesamtheit (d.h. in einem dem DWDS-Kernkorpus vergleichbaren Korpus) die Wahrscheinlichkeit, dass die relative Häufigkeit von Hund entweder nicht mehr als 12 pMW oder nicht weniger als 68 pMW beträgt, bei jeweils mindestens 1e-6 oder 0,0001% liegt und folglich, dass die Wahrscheinlichkeit, eine relative Häufigkeit innerhalb dieser zwei Grenzbereiche bei einer Suche festzustellen, bei 2e-6 oder 0,0002% liegt.

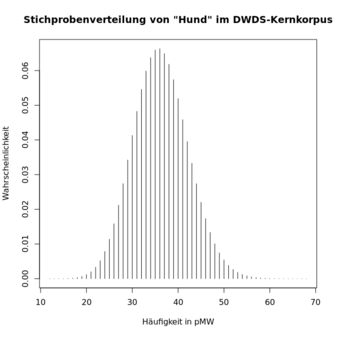
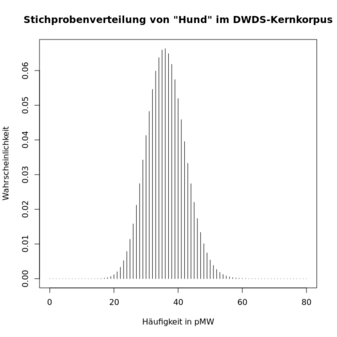
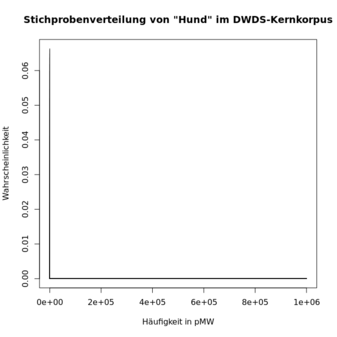
Wir können aber diese Quantile getrost auf 0 und 80 ab- bzw. aufrunden und damit alle Werte am unteren Ende berücksichtigen (kleiner als 0 geht’s ja nicht). Die zwei sich ergebenden Grafiken (die ersten zwei unten) ähneln sich sehr. Es ist auch klar zu erkennen, dass alle Quantile größer als ca. 60 eine Wahrscheinlichkeit nahe Null haben. Daher zeigt eine grafischen Darstellung aller Quantile der gewählten Stufigkeit von einer Million (die dritte Grafik unten), dass fast alle Quantile und fast die gesamte Wahrscheinlichkeit in der Nähe von 0 liegen, was die eigentlich „interessanten“ Wahrscheinlichkeiten verdeckt:

Die Erstellung der Stichprobenverteilung aus einem ermittelten Wert (z.B. der Korpushäufigkeit) ist der Ausgangspunkt für Rückschlüsse von der Stichprobe auf die zugrundeliegende Grundgesamtheit. Welche Rückschlüsse gezogen werden können, hängt von der statistischen Signifikanz des Werts, die man anhand von sogenannten Signifikanztests überprüfen kann; darauf gehen wir im letzten Themenblock des Seminars im Detail ein. An dieser Stelle sei nur noch einmal betont: Die Gültigkeit der Tests und folglich auch der Rückschlüsse, setzt die Gültigkeit der zugrundeliegenden Annahmen über die Stichprobenverteilung, wie die zwei oben erwähnten für die Binomialverteilung, voraus.

Simulierte Zufallswerte

Es ist meistens zu aufwänding (mindestens zeitlich), viele Stichproben aus einer Grundgesamtheit zu ziehen und Statistiken aus diesen mit den erwarteten Werten gemäß der Stichprobenverteilung zu vergleichen. Aber mit den r-Funktionen für die von R unterstützten Wahrscheinlichkeitsverteilungen kann man solche wiederholte Stichproben mühelos simulieren. Schon mit ca. 500 simulierten Zufallswerten kann man die Gestalt der Stichprobenverteilung gut erkennen.

Als Beispiel erstellen wir Verteilungen von Zufallswerten für unsere Zufallsvariable der Auftretenswahrscheinlichkeit von Hund im DWDS-Kernkorpus. Das Ergebnis von rbinom() ist ein Vektor von simulierten absoluten Häufigkeiten. Mit table() erstellen wir die entsprechende Häufigkeitsverteilung; da wir aber nicht die Verteilung der absoluten Häufigkeiten sondern wie bei der Stichprobenverteilung die Verteilung der Auftretenswahrscheinlichkeiten simulieren wollen, teilen wir die absoluten Häufigkeiten in der Häufigkeitstabelle durch die gewählte Anzahl der Zufallswerte und erhalten damit die relativen Häufigkeiten (die gemäß der zweiten Bedingung oben die angenommenen Auftretenswahrscheinlichkeiten sind):

Für die grafische Darstellung dieser Verteilung müssen wir nur diese Tabelle der plot()-Funktion übergeben. Durch das Argument type="h" erscheinen die Wahrscheinlichkeiten als dünne Säulen oder Stäbe ("h" steht für Histogramm, eine Art Säulendiagramm). Für den direkten Vergleich mit der oben erstellten Stichprobenverteilung wird mit dem Argument xlim=c(0,80) nur Zufallswerte zwischen 0 und 80 gezeigt (andere sind ohnehin so unwahrscheinlich, dass wir sie nicht berücksichtigen müssen). Damit die Markierung der x-Achse übersichtlich wird, unterbinden wir zunächst mit dem Argument xaxt="n" die automatische Markierung und erstellen dann mit der Funktion axis() eigene Markierungen (das Argument 1 bewirkt die Markierung der x-Achse (2 ist für die y-Achse) und das Argument at ist ein Vektor der Markierungen, hier in Zehnerschritten von 0 bis 80):

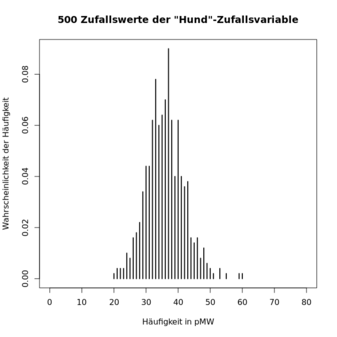
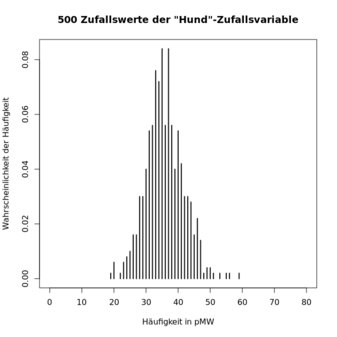
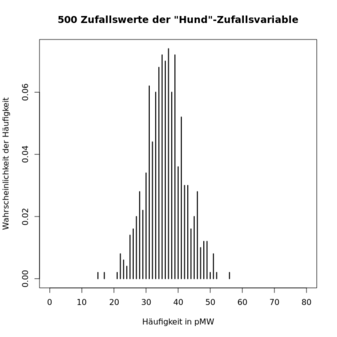
Mit jeder Wiederholung der letzten vier Eingaben wird eine neue Zufallsverteilung dieser Zufallsvariable grafisch dargestellt. Hier sind drei Beispiele, in denen die Ähnlichkeiten der zentralen Tendenz und der Streuung der Verteilungen klar erkennbar sind, aber auch die zufälligen Unterschiede, genau wie bei echten Zufallsstichproben:

Eine Folge des zentralen Grenzwertsatzes

Mit solchen Zufallsverteilungen kann man sehr schön eine Folge des zentralen Grenzwertsatzes der Wahrscheinlichkeitstheorie nachvollziehen: Wenn man in einem Zufallsexperiment eine Verteilung erstellt und daraus eine Statistik, z.B. das arithmetische Mittel, berechnet und dasselbe Experiment sehr oft wiederholt, ergibt sich eine Verteilung der Statistik, die sich bei zunehmenden Wiederholungen immer mehr einer Normalverteilung nähert (auch wenn die zugrundeliegende Verteilung keine Normalverteilung ist). Hier ist ein Beispiel anhand unserer Hund-Zufallsvariable:

Für diese Verteilung der Mittelwerte aus 10 Zufallsstichproben mit je 500 Werten liegen also 70% der Mittelwerte innerhalb von einer Standardabweichung und schon 100% innerhalb von zwei (und folglich auch innerhalb von drei) Standardabweichungen vom arithmetischen Mittel. Diese Verteilung ist also nicht genau normal aber auch nicht völlig anders. Aber es sind ja nur 10 Stichproben. Nach dem zentralen Grenzwertsatz erwarten wir bei immer mehr Stichproben eine immer genauere Annäherung an eine Normalverteilung.

Um solche Simulationen mit noch mehr Stichproben und auch mit verschiedenen Suchergebnissen aus verschiedenen Korpora einfach durchzuführen, haben wir eine R-Funktion definiert (die mit unserem source()-Aufruf in R geladen wird), am.zufall(). Diese Funktion nimmt drei Argumente, die alle Zahlen als Werte haben.

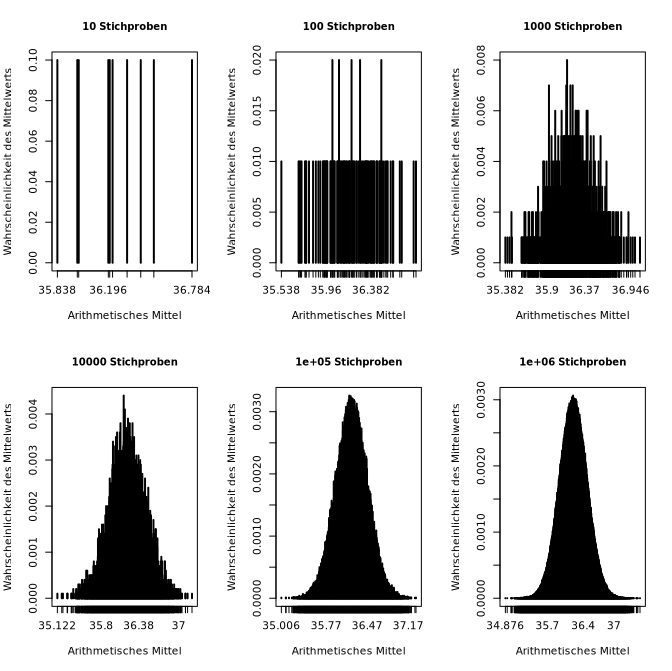
Mit folgendem Aufruf dieser Funktion werden sechs Simulationen für das Wort Hund im DWDS-Kernkorpus durchgeführt; an den Grafiken und den Zahlen ist die zunehmende Annäherung an eine Normalverteilung deutlich und schon ab 1000 Wiederholungen erkennbar (n.b.: da es sich um Zufallsverteilungen handelt, unterscheiden sich die Ergebnisse bei jeder Durchführung, bei 100.000 und einer Million Stichproben allerdings nur leicht):

← Wahrscheinlichkeitsverteilungen ↑ Sitemap Übungsaufgaben →