Hypothesentests

Ablaufschema

Hypothesentests haben im Allgemeinen folgendes Ablaufschema.

1. Man formuliert eine Arbeitshypothese über ein Merkmal oder mehrere Merkmale einer Grundgesamtheit. In der Regel behauptet die Arbeitshypothese das Auftreten eines bestimmten Effekts, was eine Änderung des aktuellen Wissensstands zur Folge hätte. Die Arbeitshypothese soll anhand einer Stichprobenstatistik (oder mehrerer Stichprobenstatistiken) überprüft werden.
   • Oft handelt es sich beim eigentlichen Forschungsgegenstand nicht um quantitative sondern um qualitative Merkmale. Man könnte z.B. eine Hypothese aufstellen über die linguistischen Merkmale, die verschiedene Schreibstile im Deutschen des 20. Jahrhunderts als mehr oder weniger formal charakterisieren. Aber für eine statistische Untersuchung muss man die Ausprägungen der Merkmale zählen und quantitativ auswerten können, was die quantitative Operationalisierung einer qualitativen Hypothese erfordert. Man könnte z.B. den Grad der Formalität des Schreibstils mit dem Anteil (in den einschlägigen Teilen der Grundgesamtheit) an Sätzen im Passiv identifizieren.
2. Man stellt der Arbeitshypothese eine sogenannte Nullhypothese gegenüber, die das Ausbleiben des vermuteten Effekts bzw. das Beibehalten des aktuellen Wissensstands behauptet. In diesem Zusammenhang heißt die Arbeitshypothese die Alternativhypothese. Üblicherweise verwendet man die Notation H0 für die Nullhypothese und H1 für die Alternativhypothese.
3. Man nimmt eine Zufallsstichprobe aus der Grundgesamtheit, ermittelt die relevante Statistik und die entsprechende Stichprobenverteilung gemäß der Nullhypothese. In diesem Zusammenhang heißt die Statistik die Teststatistik.
4. Anhand der Stichprobenverteilung berechnet man die Wahrscheinlichkeit des in der Stichprobe beobachteten Werts der Teststatistik sowie die Wahrscheinlichkeiten aller Werte der Verteilung, die noch extremer, d.h. noch weiter weg vom erwarteten Wert der Teststatistik gemäß der Nullhypothese sind, als der beobachtete Wert. Die Summe all dieser Wahrscheinlichkeiten heißt der p-Wert des Hypothesentests: Er stellt das Risiko dar, das man die Nullhypothese fälschlicherweise ablehnt.
   • Die Berechnung des p-Werts hängt von der Form der Hypothesen, insbesondere der Alternativhypothese, ab. Üblicherweise hat die Nullhypothese die Form einer Gleichung, z.B. ‚x = w‘ (also die Hypothese, dass der Wert des Merkmals (der Variable) x in der Grundgesamtheit gleich w ist). Die Alternativhypothese kann zwei allgemeine Formen annehmen: entweder als die einfache Verneinung der Nullhypothese, also die Negation der Gleichung: ‚x ≠ w‘ – dann handelt es sich um eine ungerichtete Hypothese – oder als eine der Ungleichungen ‚x < w‘ oder ‚x > w‘ – dann handelt es sich um eine gerichtete Hypothese.
     • Ein Hypothesentest, bei dem die Alternativhypothese gerichtet ist, heißt ein einseitiger Test, denn der p-Wert ergibt sich ausschließlich aus Werten von einer Seite der Stichprobenverteilung, die also alle entweder kleiner oder größer sind als der erwartete Wert der Teststatistik gemäß der Nullhypothese.
     • Ein Hypothesentest, bei dem die Alternativhypothese ungerichtet ist, heißt ein zweiseitiger Test, denn der p-Wert ergibt sich aus Werten von beiden Seiten der Stichprobenverteilung, also sowohl aus kleineren als auch aus größeren Werten als der erwartete Wert der Teststatistik gemäß der Nullhypothese.
     • Folglich ist der p-Wert bei einem zweiseitigen Hypothesentest größer als bei einem einseitigen Test und damit auch das Risiko größer, die Nullhypothese fälschlicherweise abzulehnen. Dennoch gilt im Allgemeinen die Empfehlung, einen zweiseitigen Hypothesentest zu verwenden, es sei denn, man hat gute Gründe für einen einseitigen Test (z.B. wenn wiederholte Stichproben immer nur einen Effekt in ein und derselben Richtung aufweisen).
5. Ist der p-Wert klein genug, gilt die Ablehnung der Nullhypothese und dementsprechend die Annahme der Alternativhypothese als statistisch gerechtfertigt, d.h., das Ergebnis der Stichprobe (der beobachtete Wert der Teststatistik) gilt als statistisch signifikant.
   • Diese Schlussfolgerung darf aber nicht als Beweis für die Falschheit der Nullhypothese und die Wahrheit der Alternativhypothese missverstanden werden, denn das durch den p-Wert dargestellte Risiko einer Fehlentscheidung ist nie ganz auszuschließen, weil der p-Wert auf einer Zufallsstichprobe basiert, was die Möglichkeit zulässt, dass der Wert der Teststatistik rein durch Zufall weit weg vom tatsächlichen Wert des entsprechenden Parameters der Grundgesamtheit liegt.
   • Nach der traditionellen Auffassung von Hypothesentests, soll man, um auf die statistische Signifikanz (oder Nicht-Signifikanz) der Teststatistik zu schließen, sich vor Durchführung des Hypothesentests für ein spezifisches Signifikanzniveau entscheiden: Das ist der größte Wert (in Prozent ausgedrückt), den der p-Wert haben darf, damit das Ergebnis als statistisch signifikant gilt.
   • In vielen statistischen Untersuchungen, insbesondere in den Sozial- und Geisteswissenschaften, wird traditionell ein Signifikanzniveau von 5% angenommen; d.h., ist der p-Wert 0,05 oder kleiner, gilt die Nullhypothese als abzulehnen, mit anderen Worten: Das Risiko, die Nullhypothese fälschlicherweise abzulehnen, hält man dann für gering genug, um es einzugehen.

In diesem Ablaufschema wird nur ein möglicher Fehler, den man bei der Entscheidung über die statistische Signifikanz der Teststatistik begehen kann, angesprochen: die Ablehnung der Nullhypothese, obwohl sie in Wirklichkeit (d.h. in der Grundgesamtheit) gilt (aber eben nicht in der Stichprobe). Dieser Fehler heißt der Fehler 1. Art (oder α-Fehler). Aber es gibt auch einen anderen möglichen Fehler, den Fehler 2. Art (oder β-Fehler): die Beibehaltung der Nullhypothese, obwohl in der Grundgesamtheit die Alternativhypothese gilt (aber eben nicht in der Stichprobe).

• Wenn man bei der Auswertung eines Hypothesentests den Fehler 2. Art begeht, bedeutet das, dass man den Effekt, den man eigentlich vermutet und den es tatsächlich (d.h. in der Grundgesamtheit) gibt, übersieht. Aber anders als beim Fehler 1. Art, von dem man das eingegangene Risiko durch das Signifikanzniveau festlegen kann, kann man das Risiko des Fehlers 2. Art nicht direkt steuern, weil es für die Alternativhypothese i.d.R. keinen spezifischen Wert gibt, auf den sich das Risiko beziehen könnte, sondern sehr viele mögliche Werte.
• Es gibt aber eine Reihe von Maßen und Verfahren, mit denen man versucht, die Risiken der beiden Arten von Fehler gegeneinander aufzuwiegen und möglichst zu minimieren, aber es würde den Rahmen des Seminars sprengen, näher darauf einzugehen. An dieser Stelle sei nur darauf hingewiesen, dass in diesem Zusammenhang die Stichprobengröße eine wesentliche Rolle spielt. Am Ende der nächsten Seite werden wir Beispiele des Effekts der Stichprobengröße in Bezug auf Konfidenzintervalle und statistische Signifikanz sehen.

Hypothesentests für binomialverteilte Zufallsvariablen

Es gibt viele spezifische Hypothesentests für statistische Untersuchungen, die sich in der Anzahl und Art (Skalenniveau) der untersuchten Variablen oder in der Anzahl der untersuchten Stichproben unterscheiden, die aber alle nach dem oben geschilderten Ablaufschema durchgeführt werden. Und genauso wie es eingebaute R-Funktionen für viele Wahrscheinlichkeitsverteilungen gibt, gibt es auch für viele Hypothesentests eingebaute R-Funktionen. Diese nehmen als Argumente die Stichprobenwerte sowie die Parameterwerte der zugrundeliegenden Wahrscheinlichkeitsverteilung, und berechnen damit den p-Wert, von dem man anhand des gewählten Signifikanzniveaus auf die statistische Signifikanz des Stichprobenwerts schließt; oft berechnen sie auch Konfidenzintervalle.

Weiter unten werden drei R-Funktionen vorgestellt, die für Hypothesentests mit binomialverteilten Zufallsvariablen und generell für Häufigkeiten von nominalen Variablen geeignet sind. Diese Tests spielen in korpuslinguistischen statistischen Recherchen eine wichtige Rolle, nicht zuletzt aufgrund der Annahme, dass Wortfrequenzen in Korpora durch binomialverteilte Zufallsvariablen statistisch modelliert werden können.

Es ist aber auch sinnvoll, etwas davon zu verstehen, wie die p-Werte zustandekommen und warum sie einen Rückschluss auf statistische Signifikanz ermöglichen. Das zeigen wir im Detail in den zwei folgenden Abschnitten „Berechnung des p-Werts“. Diese Erläuterungen sollen dem Verständnis dienen; aber in normalen statistischen Untersuchungen mit R (und auch in den Übungsaufgaben) verwendet man nur die spezifischen Funktionen für Hypothesentests, wie die drei, die weiter unten vorgestellt werden.

Beispiel eines Ein-Stichprobentests

Ein Ein-Stichprobentest eignet sich, um z.B. ein früheres Forschungsergebnis zu einer Eigenschaft der Grundgesamtheit anhand einer neuen Beobachtung aus einer Stichprobe zu überprüfen. Im Folgenden geben wir ein freilich unrealistisches Beispiel, um die wesentlichen Schritte der Methode möglichst genau aber auch verständlich zeigen zu können.

1. Angenommen, eine frühere Recherche hat ergeben, dass die Auftretenswahrscheinlichkeit, d.h. die relative Häufigkeit, des Wortes Hund im geschriebenen Deutsch des 20. Jahrhunderts bei 35,2 pMW liegt. Wir wollen diesen Wissensstand mit Hilfe des DWDS-Kernkorpus überprüfen, von dem wir annehmen, dass es eine repräsentative Stichprobe – also eine Zufallsstichprobe – dieser Sprachdomäne darstellt. Wir haben dazu keine qualitative Arbeitshypothese sondern es geht nur um den Vergleich zweier Werte. Wir brauchen also keine weitere Operationalisierung.
   • Für die folgenden Berechnungen sollen alle Zahlen derselben Größenordnung sein, und da die Korpusgröße und die absolute Häufigkeit des Suchergebnisses Dezimalzahlen sind, sollen daher auch die relativen Häufigkeiten nicht in pMW sondern auch als Dezimalzahlen angegeben werden: also 3.52e-05 in der von R üblicherweise verwendeten Exponentialdarstellung.
2. Da wir keinen Grund haben zu erwarten, dass der Wert aus der Stichprobe auf jeden Fall größer oder auf jeden Fall kleiner als der aktuell vorliegende Wert sein wird, sollen wir einen zweiseitigen Test durchführen, also formulieren wir folgende Null- und Alternativhypothesen:
   H0: p(Hund) = 3.52e-05
   H1: p(Hund) ≠ 3.52e-05
3. Wir ermitteln wie früher gezeigt die Korpusgröße (in Tokens) und die absolute Häufigkeit des Testwortes (Anfrage: @Hund), weisen in R diese Werte Variablen zu und berechen die relative Häufigkeit (bei Bedarf vorher unseren source-Aufruf durchführen, um freq.rel() in R zu laden):

   > kk.gr <- 121397601
> hund.kk.fa <- 4395
> (hund.kk.fr <- freq.rel(hund.kk.fa, kk.gr, "dezimal"))
[1] 3.620335e-05

   Gemäß der Annahme, dass Wortfrequenzen binomialverteilte Zufallsvariablen sind, ergibt unsere Nullhypothese eine Stichprobenverteilung basierend auf folgende Zufallsvariable:

   X ∼ B(121397601, 3.52e-05)

Berechnung des p-Werts

4. Der p-Wert ergibt sich aus der Summe der Wahrscheinlichkeit der beobachteten Häufigkeit und der Wahrscheinlichkeiten aller noch unwahrscheinlicheren möglichen Werte aus der Stichprobenverteilung. Für diese Berechnung verwenden wir die R-Funktion pbinom(), die die Verteilungsfunktion der Binomialverteilung darstellt. Da die relative Häufigkeit des beobachteten Werts (3.620335e-05) größer als die relative Häufigkeit nach der Nullhypothese (3.52e-05) ist, berechnen wir zunächst die Summe der Wahrscheinlichkeit des beobachteten Werts und der Wahrscheinlichkeiten aller größeren Werte, also die Summe der Werte am oberen Ende der Verteilung:

   > (hund.kk.pwo <- pbinom(q = hund.kk.fa - 1, size = kk.gr, prob = 3.52e-05, lower.tail = FALSE))
[1] 0.0321884

   • N.B.: Ohne das Argument lower.tail=FALSE berücksichtigt pbinom() nur Werte, die kleiner oder gleich dem Wert des ersten Arguments sind, aber mit lower.tail=FALSE werden nur die übrigen Werte berücksichtigt – also nur die, die größer als der Wert des ersten Arguments sind. 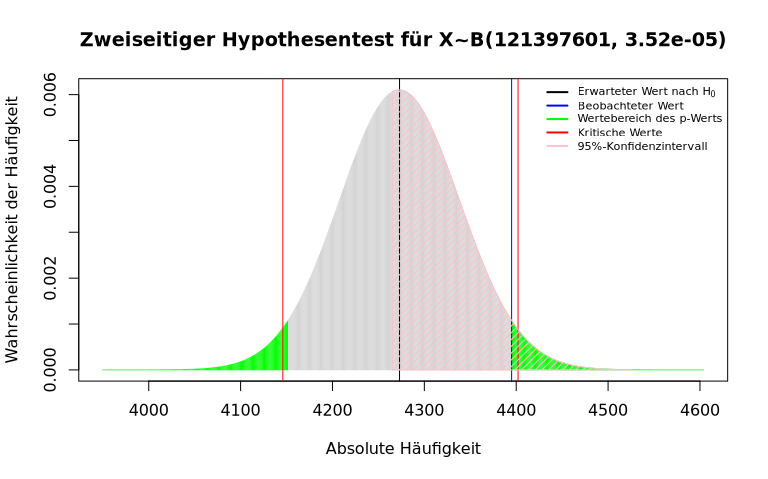Daher muss von diesem 1 abgezogen werden, damit auch die Wahrscheinlichkeit der beobachteten absoluten Häufigkeit selbst mit berechnet wird (es handelt sich um eine diskrete Verteilung, deren Werte ausschließlich ganzen Zahlen sind).

   Weil wir einen zweiseitigen Test durchführen, müssen wir auch Werte am unteren Ende der Verteilung berücksichtigen. Wäre die Stichprobenverteilung symmetrisch, würde die Summe dieser Wahrscheinlichkeiten dieselbe wie am oberen Ende sein; aber Binomialverteilungen sind nur dann symmetrisch, wenn der Parameter der Wahrscheinlichkeit p = 0,5 ist, was hier nicht der Fall ist. Es liegt aber nahe, alle Werte zu berücksichtigen, die mindestens so viel kleiner sind als der erwartete Wert gemäß der Nullhypothese, als der beobachtete Wert größer als dieser ist. Wir berechnen also die Differenz zwischen dem beobachteten und dem erwarteten Wert und ziehen diese vom erwarteten Wert ab. Dann berechnen wir mit pbinom() die Summe der Wahrscheinlichkeiten dieses Werts und aller kleineren Werte (hier hat das Argument lower.tail den Wert TRUE, und weil dieser Wert voreingestellt ist, können wir das Argument weglassen). Hier sind die R-Eingaben und -Ausgaben dieser Berechnungen:

   # Der erwartete Wert gemäß der Nullhypothese:
> (hund.kk.fe <- round(3.52e-05 * kk.gr))
[1] 4273   

   • Der erwartete Wert in einem Ein-Stichprobentest, der auf einer binomialverteilten Zufallsvariable basiert, entspricht dem Erwartungswert der Zufallsvariable, also dem Produkt der Werte der zwei Parameter der Zufallsvariable. Für die Berechnung verwenden wir auch die Funktion round(), um eine ganze Zahl zu erhalten, weil es sich ja um eine diskrete Verteilung handelt.

   # Der Wert, der kleiner als der erwartete Wert ist und denselben Abstand zu diesem hat als der ermittelte Wert:
> (hund.kk.fa2 <- hund.kk.fe - (hund.kk.fa - hund.kk.fe))
[1] 4151   
# Die Summe der Wahrscheinlichkeiten der kleineren Werte:
> (hund.kk.pwu <- pbinom(q = hund.kk.fa2, size = kk.gr, prob = 3.52e-05))
[1] 0.03087651

   Der gesuchte p-Wert ist dann die Summe dieser summierten größeren und kleineren Wahrscheinlichkeiten:

   > hund.kk.pwo + hund.kk.pwu
[1] 0.06306491
5. Damit liegt das Risiko, die Nullhypothese fälschlicherweise abzulehnen, bei ungefähr 6,3%. Wenn wir das konventionelle Signifikanzniveau von 5% für den Hypothesentest annehmen, sind wir nach der traditionellen Auffassung von Hypothesentests also nicht berechtigt, die Nullhypothese abzulehnen, d.h. die beobachtete Häufigkeit ist demnach statistisch nicht signifikant.

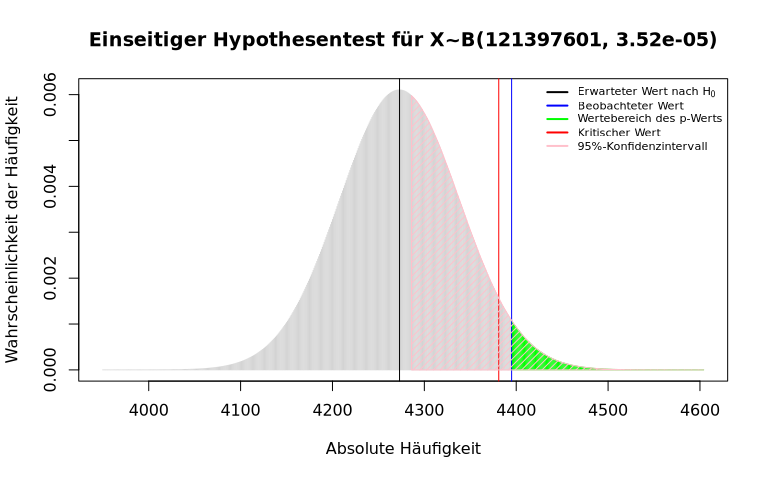
Vergleichen wir dieses Ergebnis mit dem Ergebnis des entsprechenden einseitigen Tests:

• Dementsprechend hätten wir folgende gerichtete Alternativhypothese (mit ‚>‘, weil die beobachtete Häufigkeit größer als die Häufigkeit gemäß der Nullhypothese ist):
  H1: p(Hund) > 3.52e-05.
• Der p-Wert ergibt sich demnach aus der Summe der Wahrscheinlichkeiten des beobachteten Werts 3.620335e-05 und aller größeren Werte, die wir oben schon berechnet haben:
  hund.kk.pwo ≈ 0,032
  (N.B.: Falls der beobachtete Wert kleiner als der erwartete Wert ist, wird der p-Wert für den einseitigen Test aus der Summe der Werte am unteren Ende der Verteilung ermittelt.)
• Das Risiko, die Nullhypothese fälschlicherweise abzulehnen, liegt damit bei 3,2%, also kleiner als das angenommene Signifikanzniveau von 5%.
• Damit ist das Ergebnis nach der traditionellen Auffassung von Hypothesentests statistisch signifikant und berechtigt uns dazu, die Nullhypothese abzulehnen.

Das Fazit dieses Beispiels: Hätten wir Grund zur Annahme des einseitigen Tests, würde das Ergebnis der Stichprobe als Evidenz für eine Änderung unseres Wissensstands zählen, aber ohne Grund zu dieser Annahme können wir den aktuellen Wissensstand nicht in Frage stellen.

Hier zum Abschluss dieses Beispiels sind grafische Darstellungen der zwei durchgeführten Hypothesentests, die auch entsprechende Konfidenzintervalle zeigen:

Anmerkungen:

• Der erwartete Wert gemäß der Nullhypothese ist erkennbar gleich dem Erwartungswert, also dem arithmetischen Mittel, der Stichprobenverteilung.
• Da der beobachtete Wert größer als der erwartete Wert ist, ist er der kleineste der Werte am oberen Ende der Verteilung, die den p-Wert bestimmen. (In einem Hypothesentest, in dem der beobachtete Wert kleiner als der erwartete Wert ist, ist er dementsprechend der größte der Werte am unteren Ende der Verteilung, die den p-Wert bestimmen.)
• Das angenommene Signifikanzniveau bestimmt die sogenannten kritischen Werte des Hypothesentests: die Werte, von denen die Summe ihrer Wahrscheinlichkeiten und der Wahrscheinlichkeiten aller noch extremeren Werte gleich dem Signifikanzniveau ist.
  • In einem zweiseitigen Test sind das also die Werte, die Bereiche am unteren bzw. am oberen Ende der Verteilung abgrenzt, deren Wahrscheinlichkeiten jeweils gleich der Hälfte des Signifikanzniveaus sind.
  • In einem einseitigen Test gibt es einen kritischen Wert, entweder am oberen oder am unteren Ende der Verteilung, der einen Bereich der Verteilung abgrenzt, dessen Wahrscheinlichkeit gleich dem Signifikanzniveau ist.
  Die so abgegrenzten Bereiche heißen der kritische Bereich der Verteilung für den Hypothesentest.
• Kritische Werte einer Binomialverteilung können mit qbinom() berechnet werden, für das aktuelle Beispiel also wie folgt (die erste Berechnung für den einseitigen Test, die zweite und dritte für den zweiseitigen):
  > qbinom(p = .05, size = 121397601, prob = 3.52e-05, lower.tail = FALSE)
[1] 4381
> qbinom(p = .05/2, size = 121397601, prob = 3.52e-05, lower.tail = FALSE)
[1] 4402
> qbinom(p = .05/2, size = 121397601, prob = 3.52e-05)
[1] 4146
• Liegt der beobachtete Wert innerhalb des kritischen Bereichs, gilt die Nullhypothese als abzulehnen (deswegen heißt der kritische Bereich auch der Ablehnungsbereich); liegt der beobachtete Wert außerhalb des kritischen Bereichs, gilt die Nullhypothese dementsprechend als beizubehalten. In diesen Grafiken ist gut erkennbar, dass der beobachtete Wert innerhalb des kritischen Bereichs des einseitigen Tests aber außerhalb des kritischen Bereichs des zweiseitigen Tests liegt.
• Die Grafiken lassen auch den Zusammenhang zwischen Signifikanzniveau und Konfidenzintervall gut erkennen: Beim zweiseitigen Test liegt der erwartete Wert nach der Nullhypothese innerhalb des Konfidenzintervalls, während beim einseitigen Test dieser Wert außerhalb des Konfidenzintervalls liegt.
  • Das zeigt, dass einem Signifikanzniveau von 5% ein Konfidenzniveau von 95% entspricht: Nur dann, wenn der erwartete Wert des Parameters der Grundgesamtheit gemäß der Nullhypothese außerhalb des Konfidenzintervalls liegt, gilt die Nullhypothese als abzulehnen.
  • Das Konfidenzintervall heißt auch so, weil es den Grad an Vertrauen in der Nullhypothese in diesem Sinne darstellt (Konfidenz bedeutet Vertrauen).

R-Funktionen für Hypothesentests einer binomialverteilten Zufallsvariable

Normalerweise würde man den p-Wert eines Ein-Stichprobentests für eine binomialverteilte Zufallsvariable nicht wie oben manuell in R berechnen sondern einfach mit einem Aufruf der Funktion binom.test():

• binom.test() nimmt als obligatorische Argumente:
  • die Anzahl x der Erfolge
  • die Anzahl n der Stufen (die Stichprobengröße)
  sowie als optionale Argumente:
  • die Wahrscheinlichkeit p des Erfolgs (der voreingestellte Wert ist 0,5)
  • alternative mit einem der Werte "greater" oder "less" für einen einseitigen Hypothesentest, oder dem Wert "two.sided" für einen zweiseitigen Test (letzterer ist der voreingestellte Wert).
  • conf.level mit einer Zahl als Wert des Konfidenzniveaus für die Berechnung des Konfidenzintervalls (der voreingestellte Wert ist 0.95).

Die Ausgabe dieser Funktionen ist ein kleiner Bericht über den Hypothesentest, der u.a. die Eingabedaten des Tests, den p-Wert und das Konfidenzintervall enthält. Hier sind z.B. die Ein- und Ausgaben für die obigen zwei- bzw. einseitigen Ein-Stichprobentests:

• > binom.test(hund.kk.fa, kk.gr, 3.52e-05)
  
  	Exact binomial test
  
  data:  hund.kk.fa and kk.gr
  number of successes = 4395, number of trials = 121397601, p-value = 0.06306
  alternative hypothesis: true probability of success is not equal to 3.52e-05
  95 percent confidence interval:
   3.514086e-05 3.728980e-05
  sample estimates:
  probability of success 
            3.620335e-05
  
  > binom.test(hund.kk.fa, kk.gr, 3.52e-05, alternative = "greater")
  
  	Exact binomial test
  
  data:  hund.kk.fa and kk.gr
  number of successes = 4395, number of trials = 121397601, p-value = 0.03219
  alternative hypothesis: true probability of success is greater than 3.52e-05
  95 percent confidence interval:
   3.530983e-05 1.000000e+00
  sample estimates:
  probability of success 
            3.620335e-05
   

Die p-Werte hier sind identisch mit den oben berechneten p-Werten (aber R rundet sie hier auf fünf Nachkommastellen ab bzw. auf), was darauf zurückzuführen ist, dass der Funktion binom.test() die Wahrscheinlichkeitsfunktion der Binomialverteilung zugrundeliegt. Damit sind die berechneten Wahrscheinlichkeiten zwar exakt, allerdings gibt es dazu eine Kehrseite:

• Achtung: Der Rechenaufwand beim binom.test() kann sehr hoch sein und mehr Speicher erfordern, als der Rechner zur Verfügung stellt, was zum Einfrieren oder Abbruch von R führen kann. Das kann z.B. passieren, wenn die Anzahl der Stufen (was für uns der Korpusgröße entspricht) sehr groß ist und sich die beobachtete relative Häufigkeit nur leicht von der Wahrscheinlichkeit des Erfolgs abweicht.

Falls man auf dieses Problem stößt, gibt es eine Alternative: die R-Funktion prop.test(), die viel weniger Rechenaufwand erfordert. Sie wird mit den gleichen Argumenten wie binom.test() aufgerufen und gibt einen ähnlichen Bericht über den Hypothesentest aus:

• > prop.test(hund.kk.fa, kk.gr, 3.52e-05)
  
  	1-sample proportions test with continuity correction
  
  data:  hund.kk.fa out of kk.gr, null probability 3.52e-05
  X-squared = 3.4436, df = 1, p-value = 0.0635
  alternative hypothesis: true p is not equal to 3.52e-05
  95 percent confidence interval:
   3.514469e-05 3.729378e-05
  sample estimates:
             p 
  3.620335e-05 
  
  > prop.test(hund.kk.fa, kk.gr, 3.52e-05, alternative = "greater")
  
  	1-sample proportions test with continuity correction
  
  data:  hund.kk.fa out of kk.gr, null probability 3.52e-05
  X-squared = 3.4436, df = 1, p-value = 0.03175
  alternative hypothesis: true p is greater than 3.52e-05
  95 percent confidence interval:
   3.531212e-05 1.000000e+00
  sample estimates:
             p 
  3.620335e-05 

Die p-Werte hier sind zwar keine exakten Werte wie beim binom.test() (mit prop.test() ist der p-Wert beim zweiseitigen Test etwas höher und beim einseitigen Test etwas kleiner), aber die Annäherung ist bei großen Stichproben so gut, dass die Schlussfolgerungen bezüglich statistischer Signifikanz unverändert bleiben.

• Die unterschiedlichen p-Werte ergeben sich dadurch, dass die Berechnung mit prop.test() auf der Chi-Quadrat-Verteilung basiert und verwendet die Normal-Approximation der Binomialverteilung. Die Normalverteilung ist ja eine symmetrische Verteilung, folglich ist mit prop.test() der p-Wert beim zweiseitigen Test genau doppelt so groß wie beim einseitigen Test, was mit binom.test() nicht der Fall ist.

Auch die mit binom.test() und prop.test() berechneten Konfidenzintervalle unterscheiden sich leicht voneinander, und auch von denen, die wir auf der vorigen Seite mit konfint.fr() und konfint.fr.diff() berechnet haben. Die von binom.test() und prop.test() verwendeten Berechnungen ergeben insbesondere bei kleinen Stichprobengrößen bessere Ergebnisse, sind dafür aber mathematisch komplizierter. Für die in der Korpuslinguistik üblichen Stichprobengrößen sind diese Unterschiede i.d.R. unerheblich.

Anstatt der Ausgabe als Bericht kann man den Rückgabewert von binom.test() und prop.test(), der eine Liste der Daten und Ergebnisse des Hypothesentests ist, einer Variable zuweisen und dann mit Hilfe des $-Operators auf die Elemente der Liste zugreifen. Z.B. werden mit folgenden Eingaben nur die p-Werte der obigen zwei- und einseitigen Hypothesentests ausgegeben:

• > hund.bt.2sided <- binom.test(x = hund.kk.fa, n = kk.gr, p = 3.52e-05)
> hund.bt.2sided$p.value
[1] 0.06306491
> hund.bt.greater <- binom.test(x = hund.kk.fa, n = kk.gr, p = 3.52e-05, alternative="greater")
> hund.bt.greater$p.value
[1] 0.0321884

> hund.pt1.2sided <- prop.test(x = hund.kk.fa, n = kk.gr, p = 3.52e-05)
> hund.pt1.2sided$p.value
[1] 0.06349621
> hund.pt1.greater <- prop.test(x = hund.kk.fa, n = kk.gr, p = 3.52e-05, alternative="greater")
> hund.pt1.greater$p.value
[1] 0.0317481

Beispiel eines Zwei-Stichprobentests

Mit einem Zwei-Stichprobentest kann man überprüfen, ob ein Unterschied zwischen den Stichproben bezüglich des Werts einer Variable statistisch Signifikant ist, und damit, ob die zwei Stichproben aus derselben Grundgesamtheit stammen (in Bezug auf das gemessene Merkmal). Als Beispiel betrachten wir wieder die Häufigkeit des Wortes Hund in den zwei DWDS-Korpora Kernkorpus und Berliner Zeitung als Stichproben. Wie beim Ein-Stichprobentest zeigen wir die Berechnungen der Teststatistik (die beim Zwei-Stichprobentest wesentlich komplizierter ist als beim Ein-Stichprobentest) und des p-Werts im Detail als Hintergrundwissen. Anschließend sehen wie, wie dieser Test einfach und direkt in R durchgeführt wird.

1. Die Arbeitshypothese ist, dass die zwei Stichproben aus unterschiedlichen Grundgesamtheiten (mindestens bezüglich der Verteilung des Wortes Hund) stammen. Dementsprechend ist die Nullhypothese, dass die Stichproben aus derselben Grundgesamtheit stammen.
2. Wir operationalisieren die Nullhypothese als die Gleichsetzung der Häufigkeiten des Testwortes und die Alternativhypothese als die entsprechende Ungleichung (wir führen also einen zweiseitigen Test durch):

   H0: p(Hundkk) = p(Hundbz)
   H1: p(Hundkk) ≠ p(Hundbz)

3. Wir ermitteln die Stichprobengrößen und die jeweilige absolute Häufigkeit des Testwortes:

   > kk.gr <- 121397601
> hund.kk.fa <- 4395
> bz.gr <- 237093180
> hund.bz.fa <- 7361


   Für die Bestimmung der binomialverteilten Stichprobenverteilung gemäß der Nullhypothese müssen wir einen Schätzwert für den Parameter p der Auftretenswahrscheinlichkeit in der Grundgesamtheit verwenden. Die Nullhypothese erlaubt uns, die Summe der Stichprobengrößen und die Summe der ermittelten Häufigkeiten als Werte einer größeren Stichprobe aus derselben Grundgesamtheit und die entsprechende relative Häufigkeit als die geschätzte Auftretenswahrscheinlichkeit zu betrachten:

   > (hund.kk.fa + hund.bz.fa) / (kk.gr + bz.gr)    # = (4395 + 7361)/(121397601 + 237093180) = 11756/358490781
[1] 3.279303e-05

   Somit ergibt sich die Zufallsvariable:

   X ∼ B(358490781, 3.279303e-05)

Berechnung des p-Werts

4. Die Berechnung eines exakten p-Werts für einen Zwei-Stichprobentest ist wesentlich komplizierter als beim Ein-Stichprobentest und die entsprechende R-Funktion erfordert noch viel mehr Rechenaufwand als binom.test() und ist folglich für typische korpuslinguistische Stichproben nur bedingt anwendbar; daher verwenden wir sie in diesem Seminar nicht. Aber wie beim Ein-Stichprobentest gibt es für den Zwei-Stichprobentest eine nicht-exakte Alternative, der die Chi-Quadrat-Verteilung zugrundeliegt. Für diese Alternative gibt es in R auch zwei Funktionen: die schon beim Ein-Stichprobentest vorgestellte Funktion prop.test() und die Funktion chisq.test(). Beide implementieren den in der Statistik berühmten Chi-Quadrat-Test für Kontingenztafeln. Da diese viele Anwendungen in der Statistik haben, ist es sinnvoll als Hintergrundwissen, die Berechnung des p-Werts nach dieser Methode etwas näher zu betrachten. Diese beruht auf folgenden Überlegungen:
   • Für die Berechnung des p-Werts beim Zwei-Stichprobentest muss berücksichtigt werden, dass es eben zwei beobachtete Werte gibt, deren Wahrscheinlichkeiten sowie die Wahrscheinlichkeiten der noch unwahrscheinlicheren Werte in die Berechnung eingehen.
   • Die beobachteten Werte können im Allgemeinen größer oder kleiner sein als der Wert gemäß der Nullhypothese, der wie oben gezeigt ein sich aus beiden Stichproben ergebenden Schätzwert ist.
   • Daher müssen wir wie beim Ein-Stichprobentest die Differenzen zwischen den beobachteten Werten und dem geschätzten Wert gemäß der Nullhypothese berechnen.
   • Dabei muss auch berücksichtigt werden, dass die Stichproben im Allgemeinen unterschiedliche Größen haben können, also können wir solche Differenzen nicht direkt miteinander vergleichen.
   • Aber wenn die Stichproben groß genug sind, was in der Korpuslinguistik normalerweise der Fall ist, können wir auf die Normal-Approximation der Binomialverteilung zurückgreifen und durch Standardisierung den Vergleich ermöglichen, wobei es zwei Unterschiede bei der Berechnung gibt:
     • Der z-Wert für einen beobachteten Wert fb aus einer Binomialverteilung ist: z = (fb − np) / √np(1−p), wo n die Stichprobengröße und p die Wahrscheinlichkeit des Erfolgs und folglich np der Erwartungswert und √np(1−p) die Standardabweichung der binomialverteilten Variable sind.
     • Aber der p-Wert ist eine Wahrscheinlichkeit, kann also, anders als der z-Wert bei Normalverteilungen, nicht negativ sein; deswegen quadrieren wir den z-Wert, wie bei der Berechnung von Standardabweichungen: z2 = (fb − np)2 / (np(1−p)). Damit haben wir (annähernd) eine Chi-Quadrat-Verteilung.
     • Da bei einer Binomialverteilung die Anzahl der nicht beobachteten Werte (der „Misserfolge“) fn = n − fb und die Wahrscheinlichkeit des Misserfolgs q = 1−p, ergibt sich, dass
       z2 = ((fb − np)2 / np) + ((fn − nq)2 / nq).
   • Eine solche Summe gibt es für jede (ausreichend große) Stichprobe aus einer Binomialverteilung. Dabei entsprechen den Erwartungswerten np, nq usw. die erwarteten Häufigkeiten gemäß der Nullhypothese. Wenn wir diese im Allgemeinen mit fe bezeichnen, dann ergibt sich die Teststatistik aus einer Summe von Termen der Form:
     (fb − fe)2 / fe.

   Um die erwarteten Häufigkeiten fe manuell zu berechnen, ist es praktisch, die ermittelten Werte der Stichproben in Form einer sogenannten 2×2-Kontingenztafel (auch Vierfelder-Tafel genannt) aufzustellen, die nicht nur die „Erfolge“ (in unserem Beispiel also die zwei beobachteten Häufigkeiten von Hund) sondern auch die „Misserfolge“ (die Häufigkeiten aller anderen Wortformen) enthält, damit alle Einheiten der Stichprobe berücksichtigt werden.

   Die Kontingenztafel für unser Beispiel können wir in R mit Hilfe der Funktion cbind() wie folgt erstellen (die Benennung der Spalten und Zeilen durch die Funktionen colnames() bzw. rownames() ist nicht notwendig aber verdeutlicht die anschließenden Berechnungen):

   > hund.kt <- cbind(c(hund.kk.fa, kk.gr - hund.kk.fa), c(hund.bz.fa, bz.gr - hund.bz.fa))
> colnames(hund.kt) <- c("kk", "bz")
> rownames(hund.kt) <- c("Hund", "Nicht-Hund")
> hund.kt

                     kk        bz
   Hund            4395      7361
   Nicht-Hund 121393206 237085819

   Um die erwarteten Häufigkeiten zu berechnen, brauchen wir noch die Summen der Zeilen und Spalten:

   > (hund.summe <- sum(hund.kt["Hund", ]))
[1] 11756
> (nicht.hund.summe <- sum(hund.kt["Nicht-Hund", ]))
[1] 358479025
> (kk.summe <- sum(hund.kt[ , "kk"])) # = kk.gr
[1] 121397601
> (bz.summe <- sum(hund.kt[ , "bz"])) # = bz.gr
[1] 237093180
> (kt.summe <- sum(hund.kt))
[1] 358490781

   Diese Summen können wir mit der Funktion addmargins() auch in der Kontingenztafel ausgeben:

   > addmargins(hund.kt)

                     kk        bz       Sum
   Hund            4395      7361     11756
   Nicht-Hund 121393206 237085819 358479025
   Sum        121397601 237093180 358490781

   Die erwarteten Häufigkeiten ergeben sich aus dem jeweiligen Produkt der Summe einer Zeile und der Summe einer Spalte geteilt durch die Summe beider Zeilen (oder beider Spalten – die Summen sind ja gleich):

   > (hund.kk.fe <- hund.summe * kk.summe / kt.summe)    # 11756 * 121397601 / 358490781
[1] 3980.996
> (hund.bz.fe <- hund.summe * bz.summe / kt.summe)    # 11756 * 237093180 / 358490781
[1] 7775.004
> (nicht.hund.kk.fe <- nicht.hund.summe * kk.summe / kt.summe)    # 358479025 * 121397601 / 358490781
[1] 121393620
> (nicht.hund.bz.fe <- nicht.hund.summe * bz.summe / kt.summe)    # 358479025 * 237093180 / 358490781
[1] 237085405

   Jetzt können wir die Terme (fb − fe)2 / fe der Summe der quadrierten z-Werte berechnen:

   > (hund.kk.z2 <- (hund.kk.fa - hund.kk.fe)^2 / hund.kk.fe)
[1] 43.05448
> (hund.bz.z2 <- (hund.bz.fa - hund.bz.fe)^2 / hund.bz.fe)
[1] 22.04496
> (nicht.hund.kk.z2 <- (hund.kt["Nicht-Hund", "kk"] - nicht.hund.kk.fe)^2 / nicht.hund.kk.fe)
[1] 0.001411933
> (nicht.hund.bz.z2 <- (hund.kt["Nicht-Hund", "bz"] - nicht.hund.bz.fe)^2 / nicht.hund.bz.fe)
[1] 0.000722945

   Die Summe dieser quadrierten z-Werte ist der Wert der Chi-Quadrat-Teststatistik:

   > (hund.z2.summe <- sum(hund.kk.z2, hund.bz.z2, nicht.hund.kk.z2, nicht.hund.bz.z2))
[1] 65.10158

   Und zwar handelt es sich um einen Wert aus einer Chi-Quadrat-Verteilung mit einem Freiheitsgrad. Das ist so, weil die z-Werte nicht unabhängig voneinander sind: Da die Summen der Zeilen und der Spalten festgelegt sind, werden durch Festlegung eines der Werte der Kontingenztafel alle anderen Werte auch bestimmt. Daher ist nur einer der Werte frei variierbar.

   • Im Allgemeinen kann man die Anzahl der Freiheitsgrade einer Chi-Quadrat-Verteilung mit folgender Formel bezüglich einer Kontingenztafel mit k Spalten und l Zeilen berechnen: df = (k − 1) × (l − 1).

   Der gesuchte p-Wert ist also die Wahrscheinlichkeit P(X2 ≥ 65,10158), wo X2 ∼ χ2(1) eine Chi-Quadrat-verteilte Zufallsvariable mit einem Freiheitsgrad ist. Diese Wahrscheinlichkeit können wir mit der R-Funktion pchisq() berechnen, der Verteilungsfunktion der Chi-Quadrat-Verteilung:

   > pchisq(q = hund.z2.summe, df = 1, lower.tail = FALSE)
[1] 7.113496e-16
   • N.B.: Zwar ergibt sich der p-Wert aus den Werten am oberen Ende der Chi-Quadrat-Verteilung, da sich aber eine Chi-Quadrat-Verteilung aus einer Summe von quadrierten standardnormalverteilten Zufallsvariablen ergibt, sind die Werte definitionsgemäß von beiden Enden einer Normalverteilung, was einem zweiseitigen Test entspricht.
5. Der p-Wert ist verschwindend gering und damit statistisch hoch signifikant. Wir sind also durchaus berechtigt, die Nullhypothese abzulehnen und, sofern die Annahmen des Hypothesentests gelten, den Schluss zu ziehen, dass die zwei Korpora Stichproben aus unterschiedlichen Grundgesamtheiten darstellen – jedenfalls in Bezug auf das Wort Hund.

R-Funktionen für Hypothesentests mit Kontingenztafeln

Eine solche mühsame Berechnung der Chi-Quadrat-Teststatistik und des p-Werts – macht man in der Praxis nicht in R, sondern ruft einfach die Funktion chisq.test() oder wiederum prop.test() auf:

• chisq.test() nimmt ein obligatorisches Argument x, das Daten in Form einer Kontingenztafel enthält.
• prop.test() kann auch eine Kontingenztafel als obligatorisches Argument nehmen, oder alternativ wie beim Ein-Stichprobentest die Argumente x, n, die hier aber zweistellige Vektoren der beobachteten Häufigkeiten und der Stichprobengrößen sind. (Das beim Ein-Stichprobentest obligatorische Argument p entfällt beim Zwei-Stichprobentest unter der Nullhypothese, dass die beobachteten Werte aus derselben Grundgesamtheit stammen.)
• Außerdem nehmen chisq.test() und prop.test() das optionale Argument correct. Mit dem voreingestellten Wert TRUE kann es bei kleinen Stichproben einen genaueren p-Wert ergeben, aber bei großen Stichproben, wie in der Korpuslinguistik üblich, ist eine solche Korrektur unnötig oder kann sogar irreführend sein (siehe den Chi-Quadrat-Test mit den Korpora Kernkorpus 21 und Berliner Zeitung im nächsten Abschnitt).
• prop.test() – aber nicht chisq.test() – nimmt das optionale Argument alternative mit denselben Werten wie beim Ein-Stichprobentest. Mit alternative = "greater" oder alternative = "less" wird der p-Wert bezüglich der Normalverteilung anstatt der Chi-Quadrat-Verteilung berechnet. Da die Normalverteilung symmetrisch ist, ist der p-Wert eines einseitigen Chi-Quadrat-Tests genau die Hälfte des p-Werts des entsprechenden zweiseitigen Tests.

• > chisq.test(hund.kt)
  
  	Pearson's Chi-squared test with Yates' continuity correction
  
  data:  hund.kt
  X-squared = 64.944, df = 1, p-value = 7.704e-16
  
  > prop.test(c(hund.kk.fa, hund.bz.fa), c(kk.gr, bz.gr))
  
  	2-sample test for equality of proportions with continuity correction
  
  data:  c(hund.kk.fa, hund.bz.fa) out of c(kk.gr, bz.gr)
  X-squared = 64.944, df = 1, p-value = 7.704e-16
  alternative hypothesis: two.sided
  95 percent confidence interval:
   3.866289e-06 6.446684e-06
  sample estimates:
        prop 1       prop 2 
  3.620335e-05 3.104687e-05 
  
  > chisq.test(hund.kt, correct=FALSE)
  
  	Pearson's Chi-squared test
  
  data:  hund.kt
  X-squared = 65.102, df = 1, p-value = 7.113e-16
  
  > prop.test(c(hund.kk.fa, hund.bz.fa), c(kk.gr, bz.gr), correct=FALSE)
  
  	2-sample test for equality of proportions without continuity
  	correction
  
  data:  c(hund.kk.fa, hund.bz.fa) out of c(kk.gr, bz.gr)
  X-squared = 65.102, df = 1, p-value = 7.113e-16
  alternative hypothesis: two.sided
  95 percent confidence interval:
   3.872516e-06 6.440456e-06
  sample estimates:
        prop 1       prop 2 
  3.620335e-05 3.104687e-05 

Wie man sieht, berechnen chisq.test() und prop.test() identische Chi-Quadrat-Statistiken und p-Werte. Man merke auch, dass diese Werte nur mit correct=FALSE diesselben sind wie bei der obigen manuellen Berechnung. Und schließlich berechnet nur prop.test() auch ein Konfidenzintervall für die Differenz der Häufigkeiten der Stichproben.

• N.B.: Bei sehr kleinen Stichproben, bei denen einer oder mehr der erwarteten Häufigkeiten gemäß der Nullhypothese unter 5 liegt, ist der berechnete p-Wert des Chi-Quadrat-Tests auch als Annäherung möglicherweise ungeeignet und R gibt eine entsprechende Warnung aus.

Wie beim Ein-Stichprobentest kann man den Rückgabewert dieser Funktionen einer Variable zuweisen und mit dem $-Operator auf die Elemente des Rückgabewerts, z.B. den p-Wert, zugreifen:

• > hund.x2.corrT <- chisq.test(hund.kt)    # oder: prop.test(hund.kt)
> hund.pt2.corrT <- prop.test(c(hund.kk.fa, hund.bz.fa), c(kk.gr, bz.gr))
> hund.x2.corrF <- chisq.test(hund.kt, correct=FALSE)    # oder: prop.test(hund.kt, correct=FALSE)
> hund.pt2.corrF <- prop.test(c(hund.kk.fa, hund.bz.fa), c(kk.gr, bz.gr), correct=FALSE)

> hund.x2.corrT$p.value
[1] 7.704037e-16
> hund.pt2.corrT$p.value
[1] 7.704037e-16
> hund.x2.corrF$p.value
[1] 7.113496e-16
> hund.pt2.corrF$p.value
[1] 7.113496e-16

Weitere Beispiele des Chi-Quadrat-Tests

Mehr-Stichproben-Hypothesentest

Den Chi-Quadrat-Test kann man auch auf mehr als zwei Stichproben anwenden. Wir können z.B. unser obiges Beispiel durch entsprechende Daten aus dem DWDS-Kernkorpus 21 ergänzen:

• > kk21.gr <- 15469000
> hund.kk21.fa <- 525
> hund3.kt <- cbind(hund.kt, c(hund.kk21.fa, kk21.gr - hund.kk21.fa))
> colnames(hund3.kt) <- c("kk", "bz", "kk21")
> addmargins(hund3.kt)

                    kk        bz     kk21       Sum
  Hund            4395      7361      525     12281
  Nicht-Hund 121393206 237085819 15468475 373947500
  Sum        121397601 237093180 15469000 373959781

Jetzt führen wir den Chi-Quadrat-Test durch und geben mit Hilfe des $-Operators nicht nur den p-Wert sondern auch einige andere Elemente des Rückgabewerts aus (N.B.: das Argument correct wird nur bei Kontingenztafeln mit zwei Spalten und zwei Zeilen berücksichtigt, spielt also hier keine Rolle):

• > hund3.x2 <- chisq.test(hund3.kt)
  > hund3.x2$expected    # erwartete Werte gemäß der Nullhypothese

                       kk           bz         kk21
  Hund       3.986749e+03 7.786242e+03 5.080086e+02
  Nicht-Hund 1.213936e+08 2.370854e+08 1.546849e+07

  > hund3.x2$parameter    # die Freiheitsgrade = (3-1)×(2-1)

  df 
   2

  > hund3.x2$statistic    # der Wert der Teststatistik

  X-squared 
   65.60048

  > hund3.x2$p.value    # der p-Wert
  [1] 5.689009e-15

Die Ergebnisse sind denen des obigen Zwei-Stichprobentests sehr ähnlich: Zwar ist die Teststatistik hier geringfügig größer aber bei zwei Freiheitsgraden anstatt eines, wodurch der p-Wert hier auch etwas größer ist als beim Zwei-Stichprobentest, aber dennoch so klein, dass die Nullhypothese, dass (bezüglich der Auftretenswahrscheinlichkeit des Wortes Hund) alle Stichproben aus derselben Grundgesamtheit stammen, mit großem Vertrauen abgelehnt werden kann.

Allerdings gilt diese Schlussfolgerung nur für alle drei Stichproben zusammengenommen. Oben haben wir festgestellt, dass dieselbe Schlussfolgerung auch für den Vergleich des DWDS-Kernkorpus und des Korpus der Berliner Zeitung gilt. Es bleiben aber noch die Vergleiche dieser Korpora jeweils mit dem Kernkorpus 21. Hier sind die entsprechenden Hypothesentests mit Ausgabe der p-Werte (wir verwenden hier prop.test() mit zweistelligen Vektoren, um uns die Erstellung von Kontingenztafeln zu ersparen; außerdem sieht man hier, dass der $-Operator direkt auf den Aufruf der Funktion angewendet werden kann):

• # Vergleich Kernkorpus 21 und Berliner Zeitung:
> prop.test(c(hund.kk21.fa, hund.bz.fa), c(kk21.gr, bz.gr))$p.value
[1] 0.05132178
# Vergleich Kernkorpus und Kernkorpus 21:
> prop.test(c(hund.kk.fa, hund.kk21.fa), c(kk.gr, kk21.gr))$p.value
[1] 0.1686542


Hier ist die Ablehnung der Nullhypothese in beiden Fällen statistisch nicht gerechtfertigt, wobei beim Vergleich Kernkorpus 21 und Berliner Zeitung das 5%-Signifikanzniveau nur knapp überschritten wurde. Das ist allerdings mit der Korrektur für kleine Stichproben, was hier eigentlich nicht zutrifft; ohne diese Korrektur ist der p-Wert für den Test Kernkorpus 21 und Berliner Zeitung wieder statistisch signifikant, wenn auch nur knapp:

• > prop.test(c(hund.kk21.fa, hund.bz.fa), c(kk21.gr, bz.gr), correct = FALSE)$p.value
[1] 0.04857983
> prop.test(c(hund.kk.fa, hund.kk21.fa), c(kk.gr, kk21.gr), correct = FALSE)$p.value
[1] 0.1617964


Wenn man die relativen Häufigkeiten direkt miteinander vergleicht (z.B. mit Hilfe von freq.rel()), stellt man folgende Rangordnung fest: Kernkorpus (≈36,2 pMW) > Kernkorpus 21 (≈33,9 pMW) > Berliner Zeitung (≈31,0 pMW). Dann könnte man entsprechende einseitige Tests durchführen:

• > prop.test(c(hund.kk21.fa, hund.bz.fa), c(kk21.gr, bz.gr), alternative = "greater")$p.value
[1] 0.02566089
> prop.test(c(hund.kk.fa, hund.kk21.fa), c(kk.gr, kk21.gr), alternative = "greater")$p.value
[1] 0.08432709

Während der p-Wert für den Test Kernkorpus und Kernkorpus 21 immer noch die Nullhypothese unterstützt, liegt der p-Wert für den Test Kernkorpus 21 und Berliner Zeitung nach dem 5%-Signifikanzniveau jetzt deutlich im Ablehnungsbereich. Dennoch ist der Unterschied zum extrem kleinen p-Wert für den Test Kernkorpus und Berliner Zeitung, sowie für den Test aller drei Stichproben, sehr auffällig.

Hypothesentests mit proportionalen Häufigkeiten

In den vorangehenden Beispielen ging es um den Vergleich der relativen Häufigkeiten (d.h. bezüglich der Stichprobengröße) einer Variable in zwei oder mehr Stichproben. Aber man kann mit einem Chi-Quadrat-Test auch proportionale Häufigkeiten zwischen Stichproben vergleichen. Dabei geht es um den direkten Vergleich der Werte, die sich als Ausprägungen des Merkmals auschließen, z.B. Substantive mit mehr als einer Pluralform oder Verben mit mehr als einer Form des Partizips. In solchen Fällen spielt die Korpusgröße keine Rolle, sondern die Stichprobe besteht nur aus der Gesamtheit der einzelnen Variablenwerte.

Als Beispiel nehmen wir die Verteilung nach Textklasse der Häufigkeiten der zwei Varianten des Partizips II von senden, also gesendet und gesandt, im DWDS-Kernkorpus. Wir testen also die Verteilung einer Variable mit zwei Werten in vier Stichproben (den Textklassen). Die Daten können wir am einfachsten anhand von Count-Anfragen mit dwds.data.frame() in R einlesen:

• > (gesendet.tk.kk <- dwds.data.frame(Anfrage = "count(@gesendet) #by[textClass~s/:.*//]"))
  

    Anzahl               key1
  1     31       Belletristik
  2     36 Gebrauchsliteratur
  3     46       Wissenschaft
  4     68            Zeitung

  > (gesandt.tk.kk <- dwds.data.frame(Anfrage = "count(@gesandt) #by[textClass~s/:.*//]"))
  

    Anzahl               key1
  1    217       Belletristik
  2    161 Gebrauchsliteratur
  3    107       Wissenschaft
  4    251            Zeitung 

Für die Erstellung einer Kontingenztafel aus diesen Häufigkeitstabellen verwenden wir nun nicht cbind() sondern rbind(), um die Anzahl-Spalten der Tabellen in Zeilen der Kontingenztafel umzuwandeln:

• > senden.p2.kt <- rbind(gesendet.tk.kk$Anzahl, gesandt.tk.kk$Anzahl)
> colnames(senden.p2.kt) <- gesendet.tk.kk$key1
> rownames(senden.p2.kt) <- c("gesendet", "gesandt")
> addmargins(senden.p2.kt)


           Belletristik Gebrauchsliteratur Wissenschaft Zeitung Sum
  gesendet           31                 36           46      68 181
  gesandt           217                161          107     251 736
  Sum               248                197          153     319 917

Jetzt können wir chisq.test() durchführen:

• > chisq.test(senden.p2.kt)$p.value
[1] 0.0002404428

Auch in diesem Beispiel ist der p-Wert des Hypothesentests deutlich kleiner als das traditionelle Signifikanzniveau von 5% – wenn auch bei weitem nicht so klein wie im vorangehenden Beispiel, was wohl auch mit der viel kleineren Stichprobe in diesem Fall zusammenhängt – und demnach wäre Nullhypothese, dass diese Belege von gesendet und gesandt aus derselben Grundgesamtheit stammen, abzulehnen.

Allerdings gilt wie im Beispiel im vorangehenden Abschnitt mit drei Stichproben auch hier, dass eventuelle Unterschiede bezüglich statistischer Signifikanz zwischen den Textklassen nur durch Zwei-Stichprobentests ermittelt werden können. Dazu können wir mit Hilfe von Indizierung aus dem 2×4-Kontingenztafel senden.p2.kt für jedes Paar von Textklassen eine 2×2-Kontingenztafel erstellen und auf diese chisq.test() jeweils anwenden und den p-Wert ausgeben. Dabei verwenden wir jeweils das Argument correct=FALSE, weil die Stichproben hier zwar kleiner als die Stichproben in den Beispielen mit relativen Häufigkeiten sind, gelten aber eigentlich nicht als klein im Sinne des Arguments:

• > chisq.test(senden.p2.kt[ , c("Belletristik", "Gebrauchsliteratur")], correct = FALSE)$p.value
[1] 0.09069019
> chisq.test(senden.p2.kt[ , c("Belletristik", "Wissenschaft")], correct = FALSE)$p.value
[1] 1.438285e-05
> chisq.test(senden.p2.kt[ , c("Belletristik", "Zeitung")], correct = FALSE)$p.value
[1] 0.006082423
> chisq.test(senden.p2.kt[ , c("Gebrauchsliteratur", "Wissenschaft")], correct = FALSE)$p.value
[1] 0.009782062
> chisq.test(senden.p2.kt[ , c("Gebrauchsliteratur", "Zeitung")], correct = FALSE)$p.value
[1] 0.4025996
> chisq.test(senden.p2.kt[ , c("Wissenschaft", "Zeitung")], correct = FALSE)$p.value
[1] 0.03765723

Vier der sechs Tests zeigen ein statistisch signifikantes Ergebnis gemäß dem 5%-Signifikanzniveau. Nur beim Test Belletristik-Wissenschaft ist der p-Wert sehr klein und die Ablehnung der Nullhypothese wohl zweifelsfrei berechtigt. Auffällig ist, dass nach diesen Ergebnissen die Textklassen Belletristik und Gebrauchsliteratur zumindest tendenziell und die Textklassen Gebrauchsliteratur und Zeitung mit großer Wahrscheinlichkeit jeweils zur selben Grundgesamtheit (bezüglich der getesteten Wortformen) gehören, während die Textklassen Belletristik und Zeitung wohl zu unterschiedlichen Grundgesamtheiten gehören.

Wir können schließlich auch Zwei-Stichprobentests für den Vergleich der Verteilung der Wortformen zwischen den einzelnen Textklassen und dem Gesamtkorpus durchführen. Hierzu ist es nützlich, die Kontingenztafel senden.p2.kt um die Randsummen zu ergänzen, von Letzteren brauchen wir allerdings nur die Spalte der Summen, weil diese die Gesamthäufigkeit jeder Wortform enthält (während die Zeile der Summen die Gesamthäufigkeit beider Wortformen pro Textklasse enthält, ist also für diesen Vergleich nicht geeignet):

• > senden.p2.kt2 <- addmargins(senden.p2.kt)
> chisq.test(senden.p2.kt2[1:2 , c("Belletristik", "Sum")], correct = FALSE)$p.value
[1] 0.008762995
> chisq.test(senden.p2.kt2[1:2 , c("Gebrauchsliteratur", "Sum")], correct = FALSE)$p.value
[1] 0.6377929
> chisq.test(senden.p2.kt2[1:2 , c("Wissenschaft", "Sum")], correct = FALSE)$p.value
[1] 0.003821905
> chisq.test(senden.p2.kt2[1:2 , c("Zeitung", "Sum")], correct = FALSE)$p.value
[1] 0.544924

Hier gibt es eine ziemlich deutliche Trennlinie zwischen den Textklassen Gebrauchsliteratur und Zeitung auf der einen Seite, die nach diesen Ergebnissen zur selben Grundgesamtheit wie das Gesamtkorpus gehören (bezüglich der getesteten Wortformen), und auf der anderen Seite die Textklassen Belletristik und Wissenschaft, die wohl eher aus anderen Grundgesamtheiten als das Gesamtkorpus stammen (bezüglich der getesteten Wortformen).

Es ist nicht offensichtlich, wie man die Unterschiede in diesen Ergebnissen erklären soll, insbesondere, welche Einflüsse die verschiedenen Textklassen auf die Auftretenswahrscheinlichkeit unterschiedlicher Wörter haben. Weitere korpuslinguistische (aber auch z.B. lexikographische und grammatische) Recherchen, auch mit anderen Wörtern, könnten Faktoren aufdecken, die für solche Unterschiede verantwortlich sind oder mindestens mit ihnen statistisch zusammenhängen. Wenn weitere Hypothesentests mit vielen Wörtern auch solche unterschiedliche Ergebnisse zeigen und man keine naheliegenden Faktoren dafür findet, könnte das ein Indiz sein, dass die Stichproben die notwendigen statistischen Voraussetzungen, insbesondere, dass es sich um Zufallsstichproben handelt, nicht erfüllen, mit anderen Worten: dass die Korpora nicht repräsentativ für die Sprachdomäne sind.