Wenn man dieselbe Anfrage in verschiedenen Korpora – oder in verschieden klar definierten Teilkorpora eines Korpus – durchführt, bilden die Häufigkeitsmaße, die sich aus den Suchergebnissen ermitteln lassen, zusammen genommen eine sogenannte Häufigkeitsverteilung der Häufigkeitsmaße über die Korpora bzw. Teilkorpora. Häufigkeitsverteilungen kann man auch innerhalb eines einzigen Gesamt- oder Teilkorpus bilden, wenn die Häufigkeitsmaße aus verschiedenen Ausprägungen eines bestimmten Merkmals der Korpusdaten ermittelt werden.
Häufigkeitsverteilungen sind die Grundlage für weitere statistische Auswertungen von Korpusdaten, die auch Rückschlüsse auf die Sprache, aus der die Daten stammen, ermöglichen. Im Folgenden werden wir sehen, wie Häufigkeitsverteilungen mit R erstellt und sowohl tabellarisch als auch grafisch dargestellt werden können.
Beginnen wir mit der Häufigkeitsverteilung der Wortform Hund in den frei recherchierbaren DWDS-Korpora. Um diese Häufigkeitsverteilung zu ermitteln, könnten wir die Anfrage ‚@Hund‘ in jedem Korpus durchführen, aber das DWDS-Abfragesystem erpart uns diese Mühe, denn neben der Anzeige der Suchergebnisse zur Anfrage im aktuellen Korpus stehen rechts der Suchmaske die absoluten Häufigkeiten zu dieser Anfrage in allen frei recherchierbaren Korpora:
Daher müssen wir die Anfrage nur einmal durchgeführen und können dann die
Ergebnisse als Elemente
eines Vektors mit Hilfe
der c()-Funktion
in R eingeben:
> dwds.hund.absolut <- c(4395, 525, 5158, 7361, 3670, 11448,
4173, 4990, 38, 150, 8252, 59, 334, 54)
Anmerkung:
Nun haben wir bei den Häufigkeitsmaßen schon gesehen, dass absolute Häufigkeiten für einen Vergleich zwischen unterschiedlich großen Korpora ungeeignet sind, stattdesse brauchen wir die entsprechenden relativen Häufigkeiten. Daher erstellen wir zwei weitere Vektoren, einen mit den Korpusgrößen (zur Erinnerung: diese Angaben befinden sich hier) und einen mit den entsprechenden Korpusnamen (zwecks der Zuordnung in tabellarischen und grafischen Darstellungen, siehe unten):
> dwds.korp.groesse <- c(121397601, 15469000, 150959477,
237093180, 156436295, 563306517, 108527101, 92348451, 58742778,
77565567, 75599650, 2858964, 8502921, 27012455)
>
dwds.korpora <- c("Kernkorpus", "Kernkorpus 21", "DTA-Kernkorpus",
"Berliner Zeitung", "Tagesspiegel", "Die ZEIT", "Blogs",
"DTA-Erweiterungen", "Archiv der Gegenwart", "Polytechnisches
Journal", "Filmuntertitel", "Gesprochene Sprache", "DDR", "Politische
Reden")
Anmerkungen:
Jetzt können wir mit Hilfe der selbst-definierten
Funktion freq.rel() (die Sie mit dem schon
vorgestellten source()-Aufruf
evtl. erneut in R laden müssen) einen Vektor der relativen Häufigkeiten in
pMW erstellen:
> (dwds.hund.pmw <- freq.rel(dwds.hund.absolut, dwds.korp.groesse)) [1] 36.203351 33.938845 34.168110 31.046865 23.460029 20.322861
[7] 38.451225 54.034474 0.646888 1.933848 109.153944 20.636846
[13] 39.280619 1.999078
Anmerkungen:
freq.rel() nicht nur einzelne Zahlen (wie in
den Beispielen zur
Berechnung von Häufigkeitsmaßen) sondern auch (gleich lange) Vektoren
von Zahlen sein können. In R heißen solche
Funktionen vektorisierte Funktionen: Diese operieren elementweise
auf ihren Argumenten (in diesem Fall den Vektoren der absoluten
Häufigkeiten und der Korpusgrößen) und geben einen gleich langen Vektor
der Ergebnisse (hier der jeweiligen relativen Häufigkeiten) zurück.freq.rel(freq.absolut = 7279, korp.groesse =
121397601) statt freq.rel(freq.absolut = c(7279),
korp.groesse = c(121397601)). Aber wenn der Wert eines Arguments
mehr als ein Element enthält, muss der Wert als Vektor z.B. mit Hilfe
der c()-Funktion übergeben werden.Eine tabellarische Darstellung dieser Verteilung lässt sich mit der
eingebauten Funktion data.frame() erstellen, indem wir dieser
Funktion den Vektoren der Korpusnamen und der entsprechenden relativen
Häufigkeiten als Argumente übergeben:
> data.frame(dwds.korpora, dwds.hund.pmw)
dwds.korpora dwds.hund.pmw 1 Kernkorpus 36.203351 2 Kernkorpus 21 33.938845 3 DTA-Kernkorpus 34.168110 4 Berliner Zeitung 31.046865 5 Tagesspiegel 23.460029 6 Die ZEIT 20.322861 7 Blogs 38.451225 8 DTA-Erweiterungen 54.034474 9 Archiv der Gegenwart 0.646888 10 Polytechnisches Journal 1.933848 11 Filmuntertitel 109.153944 12 Gesprochene Sprache 20.636846 13 DDR 39.280619 14 Politische Reden 1.999078
Anmerkung:
data.frame() besteht hier
aus nur einem Element, eben diese Tabelle. Die Anordnung der Häufigkeiten in dieser Tabelle entspricht einfach der Reihenfolge der oben erstellten Vektoren, die wiederum der Reihenfolge der aufgelisteten Korpora auf der DWDS-Seite der angezeigten Suchergebnisse entspricht. Eine sinnvollere Darstellung der Häufigkeitsverteilung wäre z.B. nach aufsteigender Häufigkeit, die wie folgt erstellt werden kann:
> data.frame(dwds.korpora, dwds.hund.pmw)[order(dwds.hund.pmw), ]
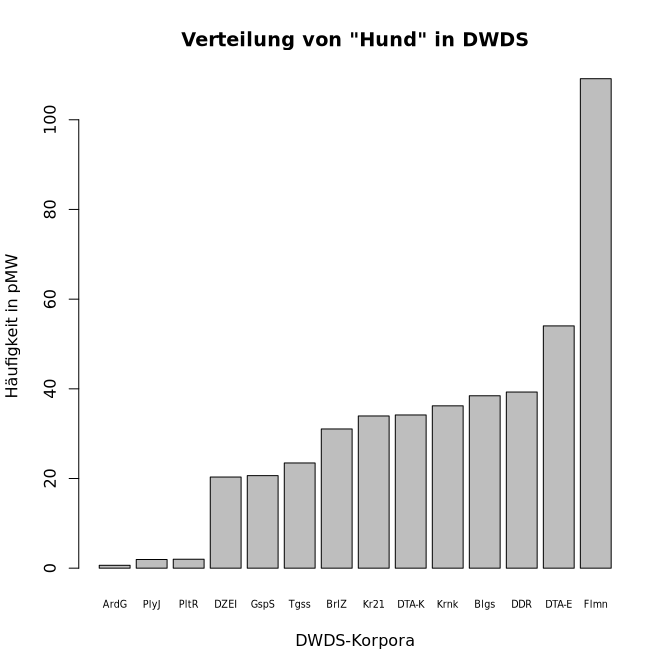
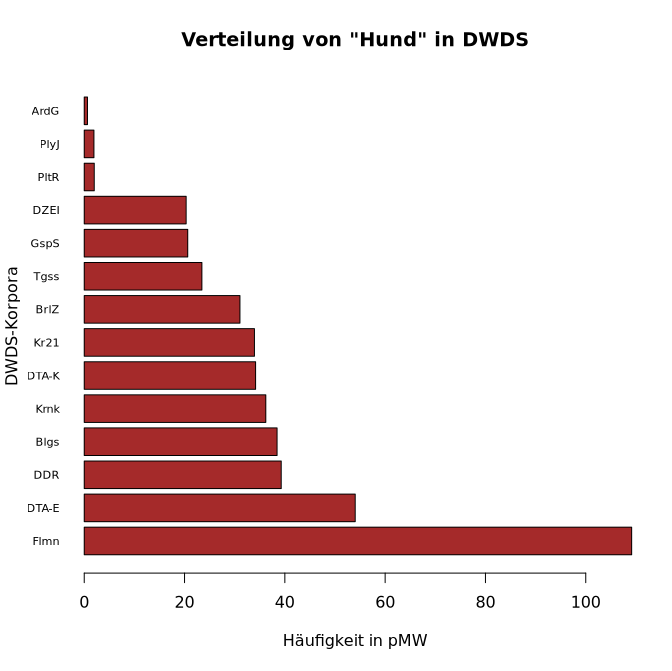
dwds.korpora dwds.hund.pmw 9 Archiv der Gegenwart 0.646888 10 Polytechnisches Journal 1.933848 14 Politische Reden 1.999078 6 Die ZEIT 20.322861 12 Gesprochene Sprache 20.636846 5 Tagesspiegel 23.460029 4 Berliner Zeitung 31.046865 2 Kernkorpus 21 33.938845 3 DTA-Kernkorpus 34.168110 1 Kernkorpus 36.203351 7 Blogs 38.451225 13 DDR 39.280619 8 DTA-Erweiterungen 54.034474 11 Filmuntertitel 109.153944
Anmerkung:
order() ordnet die Zeilen der
Tabelle gemäß den Werten ihres Arguments – hier, des
Vektors dwds.hund.pmw um, wie man an den Zeilenzahlen links
der Tabelle erkennen kann.
order() ist standardmäßig
aufsteigend, aber mit dem zweiten Argument decreasing =
FALSE ist die Sortierung absteigend.dwds.hund.pmw
ja ein Vektor von Zahlen ist. Wenn wir order()
stattdessen den Vektor dwds.korpora als (erstes)
Argument übergeben, wird die Tabelle alphabetisch sortiert.Eine alternative, wenn auch weniger übersichtliche, Darstellung der
Häufigkeitstabelle bekommt man mit Hilfe der
eingebauten names()-Funktion, wodurch die einzelnen
Häufigkeiten mit den entsprechenden Korpusnamen „benannt“
werden:
> names(dwds.hund.pmw) <- dwds.korpora
> dwds.hund.pmw
Kernkorpus Kernkorpus 21 DTA-Kernkorpus
36.203351 33.938845 34.168110
Berliner Zeitung Tagesspiegel Die ZEIT
31.046865 23.460029 20.322861
Blogs DTA-Erweiterungen Archiv der Gegenwart
38.451225 54.034474 0.646888
Polytechnisches Journal Filmuntertitel Gesprochene Sprache
1.933848 109.153944 20.636846
DDR Politische Reden
39.280619 1.999078
Auch hier kann man die Häufigkeiten z.B. in aufsteigender Reihenfolge
zeigen, allerdings mit Hilfe einer anderen Funktion
als order():
> sort(dwds.hund.pmw)
Archiv der Gegenwart Polytechnisches Journal Politische Reden
0.646888 1.933848 1.999078
Die ZEIT Gesprochene Sprache Tagesspiegel
20.322861 20.636846 23.460029
Berliner Zeitung Kernkorpus 21 DTA-Kernkorpus
31.046865 33.938845 34.168110
Kernkorpus Blogs DDR
36.203351 38.451225 39.280619
DTA-Erweiterungen Filmuntertitel
54.034474 109.153944
Anmerkung:
sort()-Funktion nimmt einen Vektor als
(erstes) Argument und sortiert dessen Elemente. Mit anderen Worten:
Diese Darstellung ist eigentlich keine Tabelle sondern eben ein Vektor
von Häufigkeiten, denen Namen zugeordnet sind, die somit eine Art
tabellarische Darstellung ergibt. Im Gegensatz dazu ist die Darstellung
durch data.frame() eine echte Tabelle und da erfolgt die
Sortierung durch Umordnung der Zeilen, was order()
bewirkt.
sort() ist die Sortierung standardmäßig
aufsteigend, aber mit dem zweiten Argument decreasing =
FALSE ist die Sortierung absteigend.dwds.hund.pmw ein Vektor von Zahlen
ist, kann sort() hier nur numerisch sortieren. Um
dennoch eine alphabetische Sortierung nach den Namen der Elemente
dieses Vektors auszugeben, musss man wiederum order()
verwenden:sort(dwds.hund.pmw)[order(dwds.korpora)]
Um die Namen der Elemente des Vektors zu löschen, geben Sie folgenden
Anweisung ein (NULL ist ein Schlüsselwort in R, dessen
Zuweisung hier die Löschung der Namen bewirkt):
> names(dwds.hund.pmw) <- NULL
Einen noch nützlicheren Einsatz als bei der Erstellung von
Häufigkeitstabellen findet die names()-Funktion bei der
grafischen Darstellung von Häufigkeitsverteilungen, wie wir jetzt sehen
werden.
Während eine Häufigkeitstabelle eine genaue quantitative Darstellung einer Häufigkeitsverteilung gibt, bekommt man üblicherweise einen einprägsameren Gesamteindruck der Häufigkeitsverteilung durch eine grafische Darstellung. Die Grafiken kann man auch mit Beschriftungen versehen, um den Informationsgehalt zu präzisieren oder ergänzen. Mit R gibt es viele Möglichkeiten der grafischen Darstellung; hier zeigen wir eine kleine Auswahl.
Für Verteilungen, die nicht zu viele Werte enthalten,
gehören Säulendiagramme oder Balkendiagramme zu den
bekanntesten Darstellungen; in R kann man diese mit
der barplot()-Funktion erzeugen.
horiz=TRUE als weiteres Argument, werden die
Häufigkeiten als Balken (also quer) dargestellt.names()-Funktion Namen zu, werden diese unterhalb der
entsprechenden Säulen bzw. links der entsprechenden Balken mit
ausgegeben. Sind die Namen allerdings länger als die Breite der Säulen
bzw. Balken, werden nicht alle gezeigt. Abhilfe schafft in diesem Fall
die abbreviate()-Funktion, die eindeutige, wenn auch nicht
immer leicht verständliche Kürzel erstellt:
> names(dwds.hund.pmw) <- abbreviate(dwds.korpora)
> names(dwds.hund.pmw)[1] "Krnk" "Kr21" "DTA-K" "BrlZ" "Tgss" "DZEI" "Blgs" "DTA-E" "ArdG" [10] "PlyJ" "Flmn" "GspS" "DDR" "PltR"
Hier sind z.B. R-Eingaben für beschriftete Säulen- und Balkendiagramme der Häufigkeitsverteilung von Hund in den DWDS-Korpora nach Häufigkeit sortiert:
> titel <- "Verteilung von \"Hund\" in DWDS"
> xlabel <- "DWDS-Korpora"
> ylabel <- "Häufigkeit in pMW"
> barplot(sort(dwds.hund.pmw), cex.names=0.6, main=titel, xlab=xlabel, ylab=ylabel)
> barplot(sort(dwds.hund.pmw, decreasing = TRUE), horiz=TRUE, cex.names=0.7, las=1, col="brown", main=titel, xlab=ylabel, ylab=xlabel)
Anmerkungen:
main wird die Grafik mit einem Titel
versehen und mit den Argumenten xlab und ylab
auch noch mit Beschriftungen der unteren bzw. linken Seite (also der x- und
y-Achsen) als Werte.
xlab und ylab vertauscht werden, weil
hier die Häufigkeiten entlang der x-Achse gezeigt werden.abbreviate() erstellten Kürzel immer noch
zu viel Platz brauchen, kann man zusätzlich das
Argument cex.names mit einer Dezimalzahl kleiner als eins
als Wert übergeben. Beim Balkendiagramm ist es auch sinnvoll, mit dem
Argument las=1 die Kürzel waage- statt senkrecht
auszugeben.
names()
zugeordneten Namen haben, kann man diese mit dem
Argument names.arg einsetzen; allerdings muss man
aufpassen, dass die Reihenfolge der Namen mit der Reihenfolge der
evtl. sortierten Häufigkeiten übereinstimmt.col mit
einem Vektor von Farbnamen als Wert. Eine Liste der eingebauten
Farbnamen gibt die colors()-Funktion aus. Bei Säulen- und
Balkendiagrammen genügt i.d.R. eine Farbe, aber z.B. bei
Tortendiagrammen (siehe unten) sind verschiedene Farben üblich.Alternativen zu den Säulen- und Balkendiagramme sind
sogenannte Dotplots, bei denen die Häufigkeiten durch Punkte statt
Säulen dargestellt werden. R bietet mit den
Funktionen dotchart() und stripchart() zwei
Varianten davon:
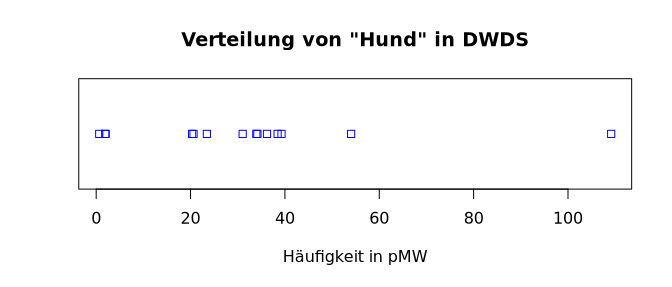
> names(dwds.hund.pmw) <- dwds.korpora
> dotchart(sort(dwds.hund.pmw), main=titel, xlab=ylabel, col="blue")
> dev.new(height=3)
> stripchart(dwds.hund.pmw, main=titel, xlab=ylabel, col="blue")
 |
 |
Anmerkungen:
xlab und ylab (also die Beschriftungen der
x- bzw. y-Achsen) vertauscht werden.dotchart() wird (anders als
bei barplot()) genug Platz für die vollen Korpusnamen
automatisch reserviert, daher müssen keine Abkürzungen verwendet werden.
Außerdem werden mit dem col-Argument nicht nut die Punkte
sondern auch die Namen farblich geändert. N.B.: Anders als
bei barplot() nimmt dotchart() kein Argument
für die Namen der Häufigkeiten, man muss diese also mit
der names()-Funktion erzeugen.
dev.new(height=3) erstellen wir ein
kürzeres Grafikfenster, weil stripchart() alle Häufigkeiten
in einem „Streifen“ (d.h. in einer Zeile) zeigt, was in
einem normalen Fensterrahmen nicht so gut aussieht. Allerdings gibt es
in dieser einzeiligen Darstellung keinen Platz für die Korpusnamen,
wodurch sie nicht so informativ ist wie die anderen Grafiken.stripchart()-Funktion erstellt automatisch eine
aufsteigende Anordnung der Häufigkeiten, daher muss der Vektor der
Häufigkeiten nicht sortiert werden.pch kann bei beiden Funktionen das
Symbol, das die Häufigkeiten darstellt, geändert werden. Der Wert
dieses Arguments kann eine Zahl sein, z.B. wird mit pch=0
ein Quadrat verwendet und mit pch=1 ein Kreis – das
sind die Voreinstellungen bei stripchart()
bzw. dotchart(), daher erscheinen sie oben so ohne Angabe
dieses Arguments. Weitere Symbole werden mit den Zahlen 2-25 verwendet.
Es it darüber hinaus möglich, Buchstaben und andere Zeichen der Tastatur
zu verwenden, allerdings müssen diese in Anführungsstriche gesetzt
werden, z.B. pch="ö", pch="@". Schließlich
sind auch Werte der Form
‚-0x⟨Codepunkt⟩‘ erlaubt, wo
⟨Codepunkt⟩ für einen sogenannten Unicode-Codepunkt steht
(diese können Sie z.B. im Internet finden). Allerdings hängt es vom
Betriebssystem und den installierten Fonts ab, welche Unicode-Codepunkte
unterstützt werden und wie sie aussehen, und man sollte es dabei nicht
übertreiben (zumal in einer Hausarbeit oder Veröffentlichung). Hier
sind zwei Beispiele (die allerdings nicht unbedingt von
wissenschaftlicher Nüchternheit zeugen):
> stripchart(sort(dwds.hund.pmw), main=titel, xlab=ylabel, pch=-0x1f415, col="blue")
> stripchart(sort(dwds.hund.pmw), main=titel, xlab=ylabel, pch=-0x1f436, col="red")
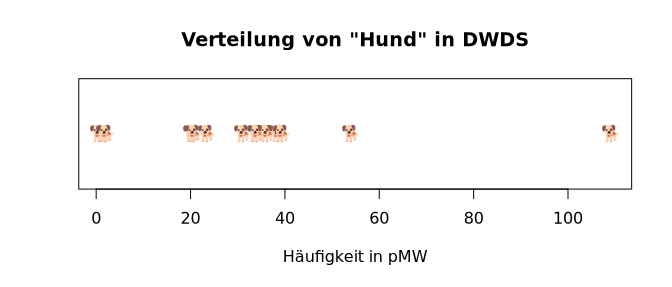 |
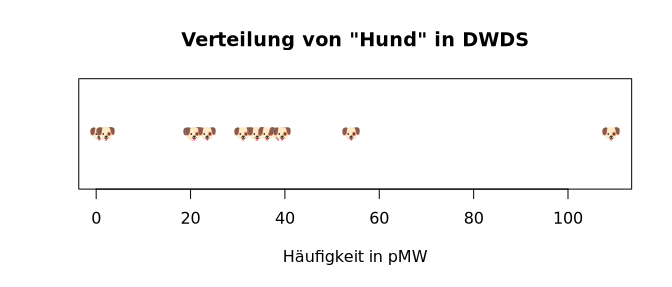 |
Um eine Häufigkeitsverteilung über Teilkorpora eines Korpus zu erstellen, müssen zum einen die Teilkorpora klar definiert und voneinander getrennt sein, damit für eine gegebene Definition jedes Token nur zu einem der Teilkorpora gehört. Zweitens müssen die Größen der Teilkorpora bekannt sein, denn nur so lassen sich die Häufigkeitsmaße der Teilkorpora in statistisch gültiger Weise miteinander vergleichen.
In DWDS kann man Teilkorpora nach den Metadaten Dekade und Textklasse spezifizieren (nach Textklasse allerdings nur bei den Referenzkorpora) und die entsprechenden Teilkorpusgrößen ermitteln, wie wir schon beim Differenzenkoeffizienten gesehen haben. (Man kann Teilkorpora in DWDS auch nach Tag (POS) bilden, das eignet sich allerdings weniger für einen Vergleich zwischen Teilkorpora als für die Erstellung von Häufigkeitsverteilungen im ganzen Korpus, siehe den nächsten Abschnitt weiter unten.)
DWDS stellt hierzu eine besondere Suchmöglichkeit zur Verfügung: Count-Anfragen (auf der DWDS-Website heißen sie Count-Abfragen). Die Ergebnisse solcher Anfragen sind keine Korpustreffer sondern nur die nach den entsprechenden Teilkorpora aufgeteilten Häufigkeiten des Suchbegriffs. Um z.B. die Häufigkeiten der Wortform Hund in den zehn Dekaden bzw. vier Textklassen des Kernkorpus zu ermitteln, kann man, statt 14mal die Anfrage ‚@Hund‘ im jeweiligen Teilkorpus durchzuführen, einfach folgende zwei Anfragen im ganzen Korpus durchführen:
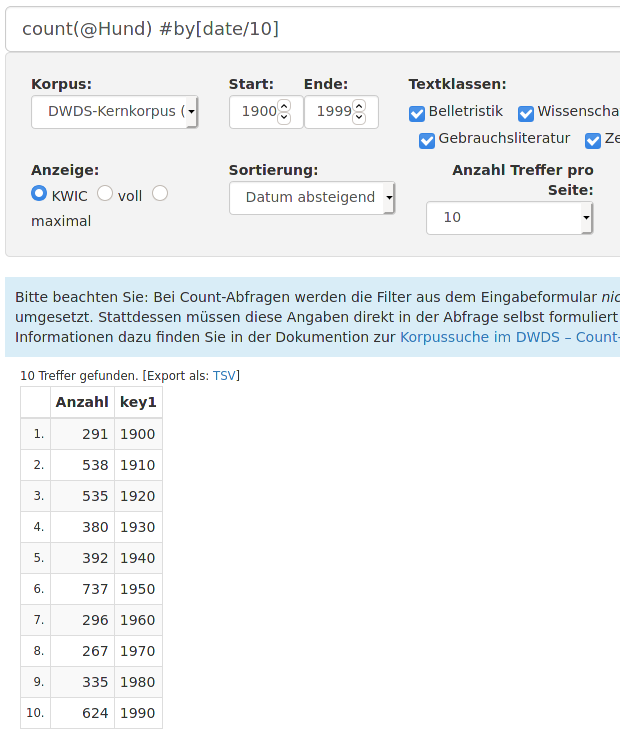 |
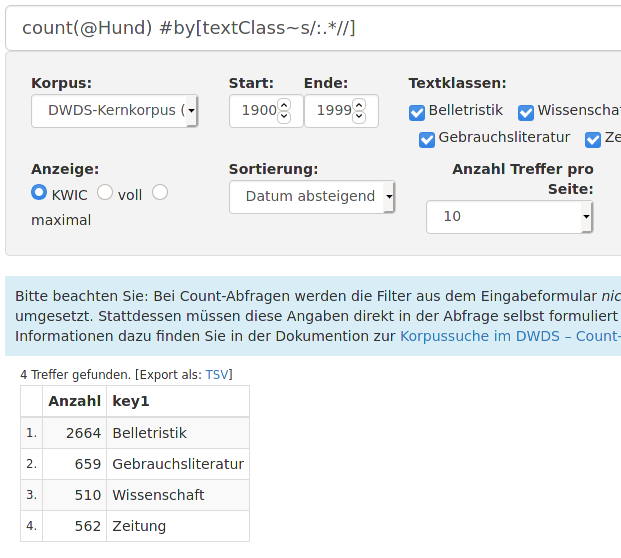 |
Die Ergebnisse dieser Anfragen zeigen die Häufigkeitsverteilungen in Form von Häufigkeitstabellen mit absoluten statt mit relativen Häufigkeiten. Man könnte die Zahlen manuell in R eingeben und dann, wie oben bei den Häufigkeitsverteilungen über verschiedene Korpora gezeigt, Verteilungen von relativen Häufigkeiten erstellen.
Aber es gibt eine bequemere Möglichkeit, bei der man die Daten nicht manuell eingeben muss (was z.B. Tippfehler vermeidet). Wenn man den Link in der Tabellenüberschrift „[Export als: TSV]“ (zu sehen in den obigen Screenshots) anklickt, dann öffnet sich eine Seite mit der Häufigkeitstabelle im Textformat:
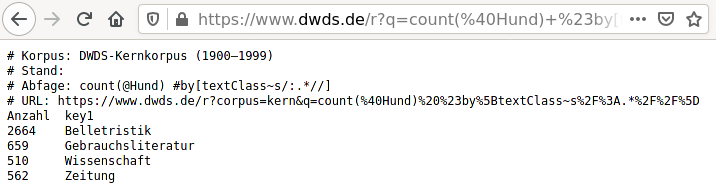
Das Format dieser Tabelle ist geeignet für das Einlesen in R mit Hilfe
der eingebauten Funktion read.table(), indem man der Funktion
die passende URL übergibt:
> hund.kk.10.tab <-
read.table("https://www.dwds.de/r?q=count(%40Hund)+%23by%5Bdate%2F10%5D&corpus=kern&date-start=1900&date-end=1999&genre=Belletristik&genre=Wissenschaft&genre=Gebrauchsliteratur&genre=Zeitung&sort=date_asc&limit=10&format=text", header=TRUE)
> hund.kk.tk.tab <- read.table("https://www.dwds.de/r?q=count(%40Hund)+%23by%5BtextClass~s%2F%3A.*%2F%2F%5D&corpus=kern&date-start=1900&date-end=1999&genre=Belletristik&genre=Wissenschaft&genre=Gebrauchsliteratur&genre=Zeitung&sort=date_asc&limit=10&format=text", header=TRUE)
Anmerkungen:
> options(HTTPUserAgent="mozilla")
read.table()-Aufrufe für den Rest der
laufenden R-Sitzung funktionieren. Allerdings müssen Sie in einer neuen
R-Sitzung diese Anweisung erneut eingeben, wenn Sie wieder
Suchergebnisse aus DWDS mit read.table() einlesen wollen.
header=TRUE
im read.table()-Aufruf bedeutet, dass die erste von R nicht
ignorierte Zeile der Datei als Kopfzeile der Tabelle gilt, die die Namen
der Spalten enthält. (R ignoriert die Tabellenzeilen, die mit
‚#‘ beginnen.)Hier ist die R-Ausgabe der so eingelesenen Tabellen:
> hund.kk.10.tab Anzahl key1
1 291 1900
2 538 1910
3 535 1920
4 380 1930
5 392 1940
6 737 1950
7 296 1960
8 267 1970
9 335 1980
10 624 1990
> hund.kk.tk.tab Anzahl key1
1 2664 Belletristik
2 659 Gebrauchsliteratur
3 510 Wissenschaft
4 562 Zeitung
Für die Berechnung von relativen Häufigkeiten brauchen wir auch noch die Teilkorpusgrößen. Die entsprechenden Angaben können Sie hier abrufen, indem Sie die gewünschten Eigenschaften auswählen und auf den Button „Statistik abfragen“ klicken. Dann erscheinen die entsprechenden Häufigkeitstabellen darunter:
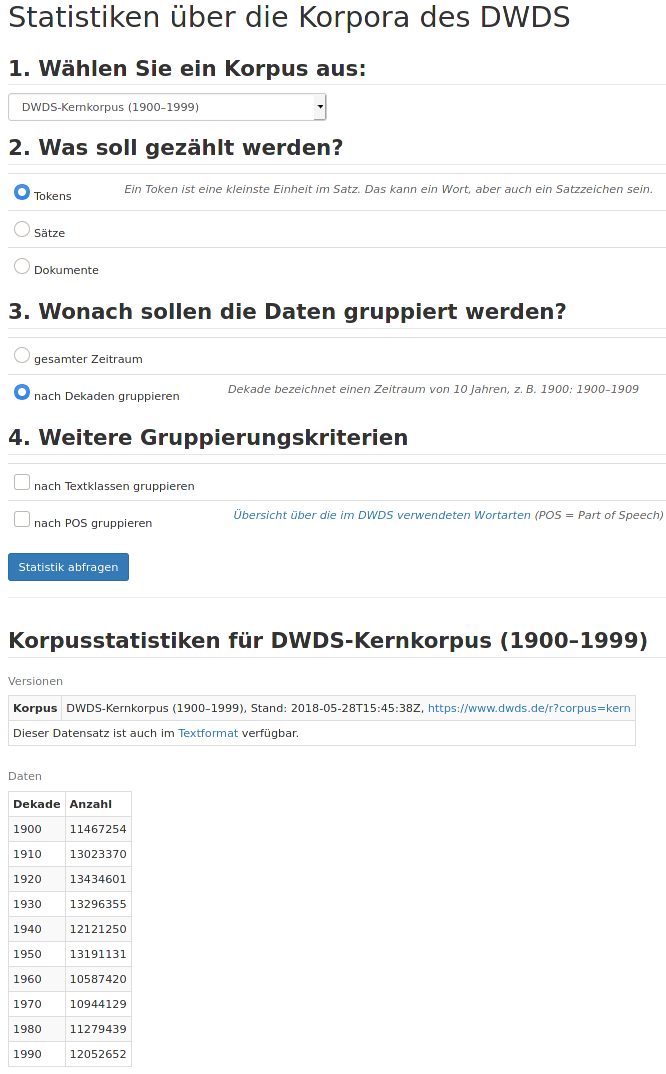 |
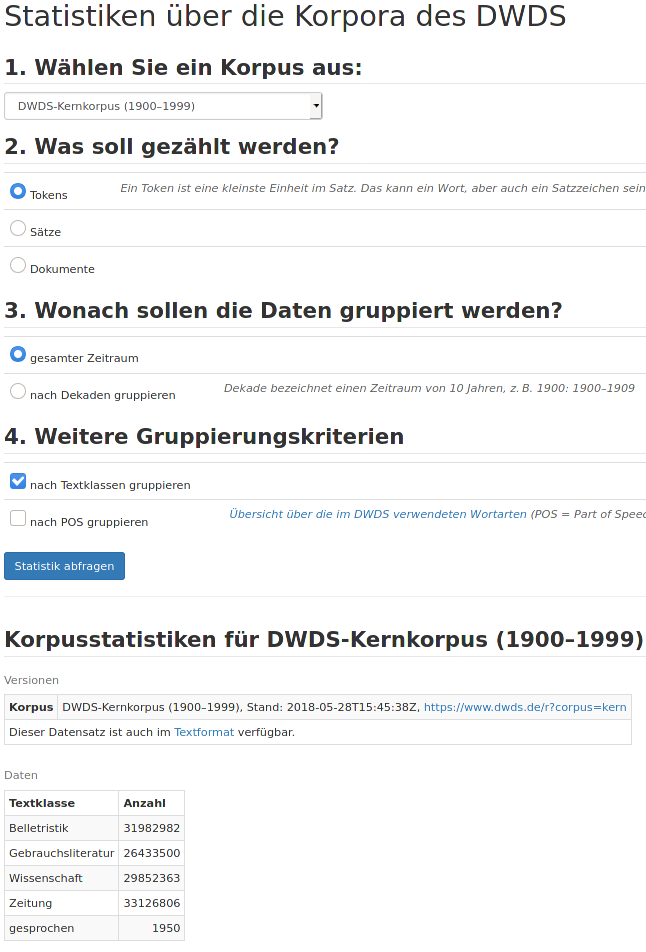 |
Auch diese Tabellen können Sie über den darüber stehenden Link
„Textformat“ mit read.table() in R laden (Sie
müssen genau wie oben darauf achten, die korrekte URL als Argument zu
übergeben):
> kk.10.tab <- read.table("https://www.dwds.de/r/stat?corpus=kern&cnt=tokens&date=decade&format=text", header=TRUE)
> kk.tk.tab <- read.table("https://www.dwds.de/r/stat?corpus=kern&cnt=tokens&date=all&textclass=1&format=text", header=TRUE)
> kk.10.tab Dekade Anzahl
1 1900 11467254
2 1910 13023370
3 1920 13434601
4 1930 13296355
5 1940 12121250
6 1950 13191131
7 1960 10587420
8 1970 10944129
9 1980 11279439
10 1990 12052652
> kk.tk.tab Textklasse Anzahl
1 Belletristik 31982982
2 Gebrauchsliteratur 26433500
3 Wissenschaft 29852363
4 Zeitung 33126806
5 gesprochen 1950
Anhand dieser vier Häufigkeitstabellen hund.kk.10.tab, kk.10.tab,
hund.kk.tk.tab und kk.tk.tab wollen wir nun die relativen Häufigkeiten der
Teilkorpora mit der Funktion freq.rel() berechnen. Aber
dafür müssen die Angaben in den Spalten der Tabellen in Form von Vektoren
zur Verfügung stehen, weil die Argumente von freq.rel()
Vektoren sind. Diese Umwandlung machen die folgenden Eingaben (auf solche
Eingaben gehen wir im 4. Themenblock ausführlich ein), wie man an den
Ausgaben sieht:
> hund.kk.10.tab$Anzahl [1] 291 538 535 380 392 737 296 267 335 624 > hund.kk.10.tab$key1 [1] 1900 1910 1920 1930 1940 1950 1960 1970 1980 1990 > hund.kk.tk.tab$Anzahl [1] 2664 659 510 562 > hund.kk.tk.tab$key1 [1] "Belletristik" "Gebrauchsliteratur" "Wissenschaft" [4] "Zeitung" > kk.10.tab$Anzahl [1] 11467254 13023370 13434601 13296355 12121250 13191131 10587420 10944129 [9] 11279439 12052652 > kk.10.tab$Dekade [1] 1900 1910 1920 1930 1940 1950 1960 1970 1980 1990 > kk.tk.tab$Anzahl[1:4] [1] 31982982 26433500 29852363 33126806 > kk.tk.tab$Textklasse[1:4] [1] "Belletristik" "Gebrauchsliteratur" "Wissenschaft" [4] "Zeitung"
Anmerkung:
Diese Bezeichner für die Vektoren sind allerdings etwas umständlich und teilweise redundant (nämlich, die Bezeichner für die Namen der Dekaden und der Textklassen). Daher ersetzen wir sie durch lesbarere Variablennamen mit folgenden Zuweisungen:
> hund.kk.10.fa <- hund.kk.10.tab$Anzahl
> hund.kk.tk.fa <- hund.kk.tk.tab$Anzahl
> kk.10.fa <- kk.10.tab$Anzahl
> kk.tk.fa <- kk.tk.tab$Anzahl[1:4]
> kk.10 <- hund.kk.10.tab$key1 # identisch mit kk.10.tab$Dekade
> kk.tk <- hund.kk.tk.tab$key1 # identisch mit kk.tk.tab$Textklasse[1:4]
Nach all diesen vorbereitenden Schritten berechnen wir schließlich die
relativen Häufigkeiten von Hund in den Teilkorpora und erstellen
dann mit data.frame() die entsprechenden
Häufigkeitstabellen:
> hund.kk.10.pmw <- freq.rel(hund.kk.10.fa, kk.10.fa)
> hund.kk.tk.pmw <- freq.rel(hund.kk.tk.fa, kk.tk.fa)
> data.frame(kk.10, hund.kk.10.pmw) kk.10 hund.kk.10.pmw
1 1900 25.37661
2 1910 41.31035
3 1920 39.82254
4 1930 28.57926
5 1940 32.33990
6 1950 55.87087
7 1960 27.95771
8 1970 24.39664
9 1980 29.70006
10 1990 51.77284
> data.frame(kk.tk, hund.kk.tk.pmw) kk.tk hund.kk.tk.pmw
1 Belletristik 83.29430
2 Gebrauchsliteratur 24.93049
3 Wissenschaft 17.08407
4 Zeitung 16.96511
Und hier ist auch die alternative tabellarische Darstellung mit Hilfe
der names()-Funktion:
> names(hund.kk.10.pmw) <- kk.10
> names(hund.kk.tk.pmw) <- kk.tk
> hund.kk.10.pmw 1900 1910 1920 1930 1940 1950 1960 1970
25.37661 41.31035 39.82254 28.57926 32.33990 55.87087 27.95771 24.39664
1980 1990
29.70006 51.77284
> hund.kk.tk.pmwBelletristik Gebrauchsliteratur Wissenschaft Zeitung
83.29430 24.93049 17.08407 16.96511
Auch Häufigkeitsverteilungen über Teilkorpora können natürlich grafisch dargestellt werden. Wir zeigen hier zwei weitere Diagramme, das Tortendiagramm (auch Kreisdiagramm genannt) und das Liniendiagramm, sowie einige zusätzliche grafische Gestaltungsmöglichkeiten von R:
> dev.new(width=9, height=5)
> op <- par(mfrow = c(1,2))
> pie(hund.kk.tk.pmw, col=rainbow(4), labels=paste0(kk.tk, "\n", round(hund.kk.tk.pmw, 1), " pMW"), cex=0.7, main="Verteilung von \"Hund\" nach Textklasse", cex.main=0.9)
> plot(kk.10, hund.kk.10.pmw, type="b", pch=21, bg="green", xaxp=c(1900, 1990, 9), cex.axis=0.5, xlab="", ylab="Häufigkeit in pMW", cex.lab=0.7, main="Verteilung von \"Hund\" nach Dekade", cex.main=0.9)
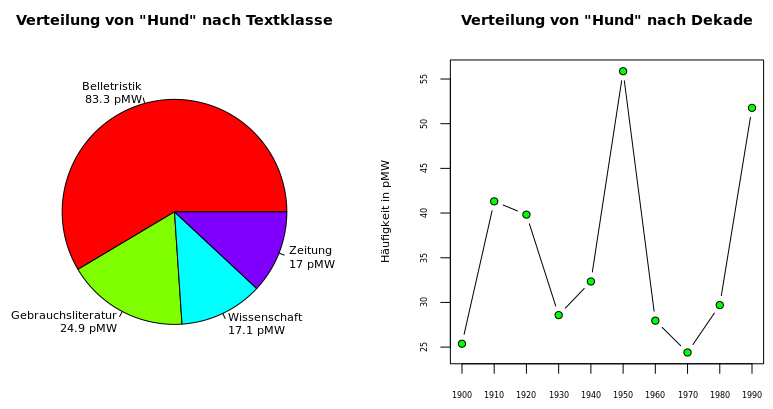
Anmerkungen:
barplot(), pie(), plot()
usw. ein schon geöffnetes Grafik-Fenster wieder, d.h. jeder Aufruf
überschreibt das Fenster. Will man mehrere Diagramme in einem
Grafik-Fenster erstellen, kann man wie folgt vorgehen:
dev.new() ein neues leeres Grafik-Fenster, in
dem der nächste Aufruf einer Grafik-Funktion ein Diagramm erzeugt.
Die Argumente width und height bestimmen
die Breite bzw. Höhe des Fensters (in Zoll).par() kann man viele Eigenschaften
des Grafik-Fensters ändern, z.B. mit dem Argument mfrow =
c(1,2) können zwei Diagramme nebeneinander in einem
Grafik-Fenster erzeugt werden, oder mit mfrow=c(2,2)
vier Diagramme neben- und untereinander, usw.par() kann man die bisher geltenden
Eigenschaften durch Zuweisung an eine Variable (im obigen Beispiel
op) speichern. Wenn man diese Eigenschaften in einem
offenen Grafik-Fenster wiederherstellen will, ruft
man par(op) auf; dieser Aufruf ist nicht erforderlich,
falls das Grafik-Fenster vor dem nächsten Grafik-Aufruf geschlossen
wird.labels hinzufügen, wie oben gezeigt.
labels ist eine Zeichenkette, in diesem
Beispiel durch die Funktion paste0 erzeugt, die
beliebig viele Zeichenketten als Argumente nimmt und sie zu einer
Zeichenkette verbindet. In diesem Beispiel sind die Argumente die
Namen der Textklassen (kk.tk), ein Zeilenumbruch
("\n", und die relativen Häufigkeiten (auf höchstens
eine Nachkommazahl gerundet) in pMW).col ändern.
In diesem Beispiel verwenden wir die
Funktion rainbow(), die eine ganze Zahl n als
Argument nimmt und einen Vektor mit n Bezeichnern (als
Hexadezimalzahlen) von Regenbogenfarben zurückgibt (in diesem
Beispiel also die ersten vier Regenbogenfarben).plot()-Funktion sind
Vektoren der x- bzw. y-Koordinaten, also von Werten entlang der x-
bzw. y-Achse, hier die Dekaden und Häufigkeiten des Suchbegriffs;
das Argument type bestimmt die Art des Diagramms: Der
voreingestellte Wert ist "p", was nur Punkte zeigt; "l" zeigt nur
Linien und "b" zeigt beides, also sowohl Punkte als auch die sie
verbindenden Linien.pch
ändern (wie bei dotchart()
und stripchart()); der hier verwendete Kreis kann mit
dem Argument bg farblich ausgefüllt werden.xaxp können numerische Werte der
Markierungen entlang der x-Achse bestimmt werden, indem man dem
Argument einen Vektor zuweist, der die Start- und Endwerte sowie die
Anzahl der Intervalle zwischen diesen Werten enthält (ohne das
Argument xaxp erstellt R Markierungen automatisch, aber
normalerweise wird nicht bei jeder Markierung der entsprechende Wert
in der Grafik angezeigt). Das Argument cex.axis=0.5
verkleinert die Dekaden-Angaben, damit sie alle erscheinen. Das
Argument xlab="" lässt eine Beschriftung der x-Achse
weg, weil sie mit den Dekaden-Angaben überflüssig wäre.Auch innerhalb eines einzelnen Gesamt- oder Teilkorpus kann man Häufigkeitsverteilungen erstellen, und zwar Verteilungen von Merkmalen der Korpusdaten oder -metadaten. Beispiele sind grammatische Merkmale wie Flexionsvarianten eines Lemmas, die verschiedenen Wortarten insgesamt (z.B. Nomen, Verb, Adjektiv usw.) oder die Realisierungen einer Wortart (z.B. die Formen eines Pronomens), die Ausprägungen von Genus (Femininum, Maskulinum, Neutrum), Numerus (Singular, Plural) oder Kasus (Nominativ, Akkusativ usw.), auch komplexe syntaktische Eigenschaften wie z.B. Funktionsverbgefüge oder die Stellung von Modalpartikeln im Satz; numerische Merkmale wie Wortlänge (in Zeichen) und Satzlänge (in Wörtern); und auch Metadaten wie Textklasse, Entstehungszeit (Dekade, Jahr), Quelle usw.
Ob die Häufigkeitsverteilung eines gegebenen Merkmals in einem gegebenen Korpus oder Teilkorpus erstellt werden kann, hängt nicht nur von der Aufbereitung des Korpus sondern auch vom Abfragesystem ab. Die DWDS-Korpora haben z.B. keine Annotatationen für Genus, Numerus oder Kasus, also kann man Anfragen zu diesen Merkmalen nicht mit Hilfe von Tags formulieren. Auch strukturelle Eigenschaften wie Funktionsverbgefüge und Wortstellung sind in der DWDS-Anfragesprache nur begrenzt suchbar.
Auf der anderen Seite sind Häufigkeitsverteilungen der Tokens (und auch
der Sätze und der Dokumente) eines Korpus nach Textklassen oder Dekade in
DWDS einfach abfragbar, wie wir im
Zusammenhang mit Teilkorpusgrößen gesehen haben. Und genauso einfach kann
man Häufigkeitsverteilungen der Wortarten in DWDS erstellen, indem auf
dieser Seite die Checkbox „nach POS gruppieren“ (unter
„4. Weitere Gruppierungskriterien“) anklickt. Und wie bei den
Textklassen und Dekaden kann auch die Häufigkeitstabelle der Wortarten
mit read.table() in R einlesen
(bei Übergabe der passenden URL).
Darüber hinaus kann man in DWDS mit Hilfe von Count-Anfragen Häufigkeitsverteilungen von Suchbegriffen nicht nur nach Textklasse oder Dekade erstellen, sondern auch nach anderen Merkmalen. Ein einfaches Beispiel ist die nach Häufigkeit absteigend sortierte Verteilung der Flexionsvarianten des Lemmas Hund im Kernkorpus:
count(Hund) #by[$w] #DESC_COUNT
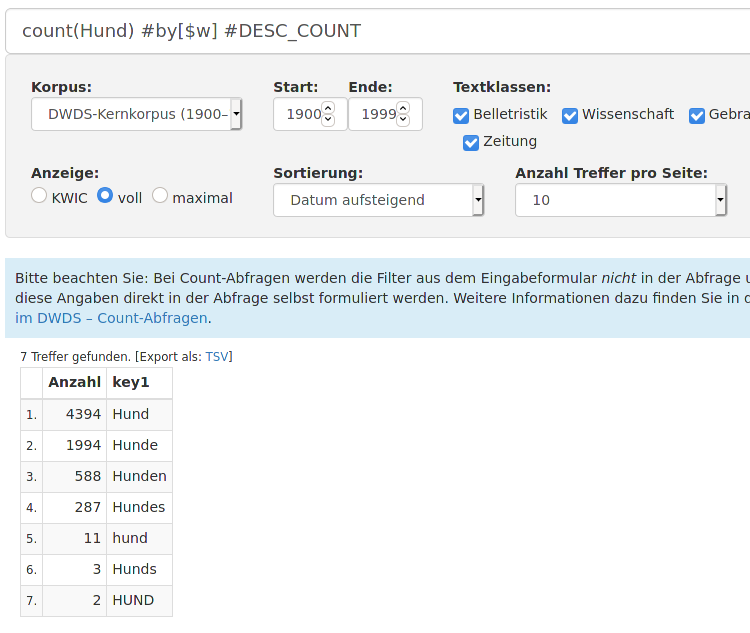
Allerdings stößt man dabei schnell an die Grenzen der Verwendbarkeit von Count-Anfragen, wie folgende Beispiele zeigen:
count($p=PPER) #by[$w] #DESC_COUNT
count(*) #by[$w] #DESC_COUNT
Zum Schluss zeigen wir ein Beispiel für die Häufigkeitsverteilung eines numerischen Merkmals, Wortlänge in Zeichen. Die DWDS-Anfragesprache bietet zwar keine Möglichkeit in einer einzigen Anfrage sämtliche Wortlängen zu suchen, aber man kann sehr wohl nach spezifischen Wortlängen suchen, und damit kann man mit etwas Mühe und Geduld alle Wortlängen in einem Korpus quantitativ erfassen.
Zunächst nehmen wir aus Gründen der Einfachheit an, dass Wortformen nur aus Buchstaben bestehen (dass diese Annahme nicht stimmt, zeigen Wortformen wie z.B. ‚2020‘, ‚2000er‘ und ‚deutsch-französich‘; man könnte die folgenden Anfragen ergänzen, um solcher Wortformen zu finden, aber wir verzichten hier darauf). Mit Hilfe von regulären Ausdrücken, und insbesondere der Zeichenklasse ‚[[:alpha:]]‘, formulieren wir folgende Anfragen, die alle Wortformen jeweils aus einem, zwei, drei, …, n Buchstaben finden:
/^[[:alpha:]]$//^[[:alpha:]]{2}$//^[[:alpha:]]{3}$//^[[:alpha:]]{n}$/Man führt diese Anfragen durch und hält die jeweils angezeigte absolute Häufigkeit fest, bis die Anfrage für die Wortlänge n keine Treffer findet, was bedeutet, dass die Wortlänge n die absolute Häufigkeit 0 im Korpus hat. Dann gibt man folgende Anfrage (mit der tatsächlich verwendeten Zahl anstelle von n) ein:
/^[[:alpha:]]{n}[[:alpha:]]+$/Diese Anfrage sucht Wortformen, die aus mindestens n+1 Buchstaben bestehen. Wenn diese Anfrage Treffer findet, dann handelt sich bei der Wortlänge n um eine Lücke und man führt weitere Anfragen für n+1, n+2 Buchstaben usw. durch, bis es wieder keine Treffer gibt. Erst, wenn eine Anfrage wie in (*) keine Treffer findet, weiß man, dass die längste Wortform im Korpus aus n−1 Buchstaben besteht.
In dieser Weise habe ich die Häufigkeitsverteilungen der Wortlängen im DWDS-Kernkorpus und Kernkorpus 21 ermittelt und als Vektoren in R angelegt:
> wl.kk <- c(249194, 7294250, 27418144, 11200530, 11100706, 9727361, 6454337, 5396133, 4852525, 3932445, 3221868, 2317834, 1606705, 1160252, 782895, 546142, 382466, 277872, 186176, 129702, 84877, 58323, 41422, 25099, 18221, 10167, 7423, 3729, 2399, 1267, 846, 417, 277, 176, 117, 76, 41, 32, 22, 11, 10, 8, 6, 4, 6, 3, 3, 0, 4, 1, 2, 1, 1, 0, 3, 0, 2, 1, 7, 0, 2, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1)
> wl.kk21 <- c(24456, 885495, 3398136, 1564988, 1419213, 1201745, 846764, 694847, 590883, 473723, 378665, 257501, 189927, 135387, 89557, 60100, 45283, 31874, 23228, 15102, 11615, 7313, 5097, 3536, 2420, 1286, 899, 440, 283, 119, 74, 55, 22, 20, 11, 12, 3, 5, 8, 2, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1)
Der Vektor wl.kk enthält 90 Elemente und der
Vektor wl.kk21 enthält 63 Häufigkeiten. Nach der oben
geschilderten Vorgehensweise bedeutet das, dass die längste Wortform im
Kernkorpus aus 90 Buchstaben besteht und die längste im Kernkorpus 21 aus
63 Buchstaben, und diese Wortformen kommen jeweils nur einmal vor; aber es
gibt z.B. keine Wortform im Kernkorpus aus genau 89 Buchstaben und keine
im Kernkorpus 21 aus genau 62 Buchstaben.
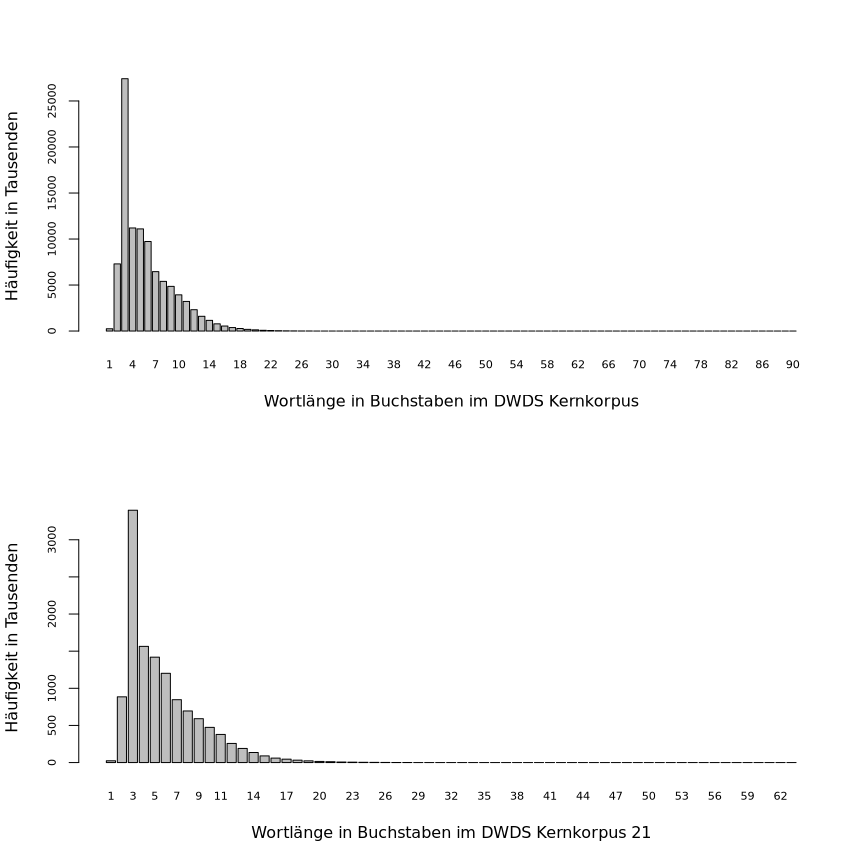
Tabellarische Darstellungen von diesen Häufigkeitsverteilungen in R sind aufgrund der vielen Einträge nicht sehr anschaulich, grafische Darstellungen dagegen schon eher:
> xlabel <- "Wortlänge in Buchstaben im DWDS Kernkorpus"
> ylabel <- "Häufigkeit in Tausenden"
> dev.new(width=9, height=9)
> op <- par(mfrow = c(2,1))
> barplot(wl.kk/1e3, names.arg = 1:length(wl.kk), cex.names = 0.7, cex.axis = 0.7, xlab = xlabel, ylab = ylabel)
> barplot(wl.kk21/1e3, names.arg = 1:length(wl.kk21), cex.names = 0.7, cex.axis = 0.7, xlab = paste(xlabel, "21"), ylab = ylabel)
Anmerkungen:
par(mfrow = c(2,1)) werden zwei Grafiken vertikal
ausgegeben im Grafikfenster.
barplot()-Aufrufen sind die Elemente der Vektoren
der Häufigkeiten durch 1000 (1e3) geteilt, damit die Zahlen entlang der
y-Achse lesbarer sind; deshalb die Beschriftung „Häufigkeit in
Tausenden“. Also hat z.B. die Wortlänge 4 im Kernkorpus eine
Häufigkeit von ca. 11000 × 1000 = ca. 11 Mio. und im Kernkorpus 21
ca. 1500 × 1000 = ca. 1,5 Mio.names.arg erstellt: ein Vektor von 1 bis zur
jeweils größten Wortlänge (90 Buchstaben im Kernkorpus, 63 im Kernkorpus
21). Aus Platzgründen wird nicht jede einzelne Wortlänge an der x-Achse
angezeigt.paste() im
zweiten barplot()-Aufruf is wie paste0() aber
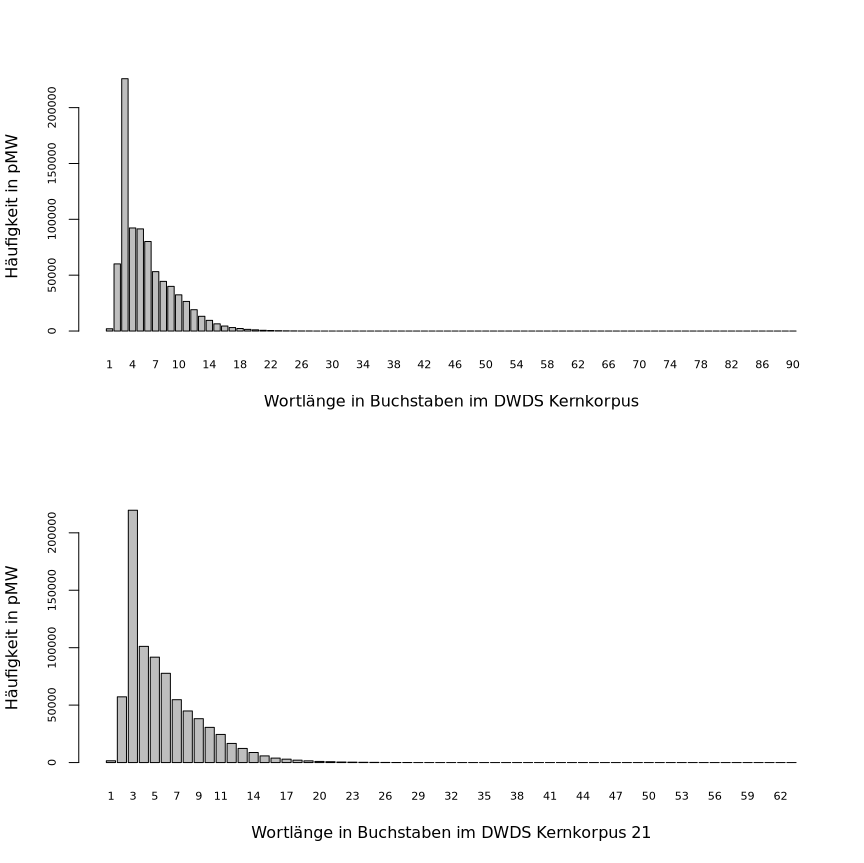
fügt ein Leerzeichen zwischen den Argumenten hinzu.Diese Grafiken machen deutlich, dass die Häufigkeitsverteilungen der Wortlängen im Kernkorpus und im Kernkorpus 21 von der Gestalt her sehr ähnlich sind aber unterscheiden sich stark in absoluten Häufigkeiten, was wohl mit den sehr unterschiedlichen Korpusgrößen zusammenhängt. Diese Vermutung bestätigt sich, wenn wir statt der absoluten Häufigkeiten die relativen Häufigkeiten in pMW grafisch darstellen: Die Gestalten sind unverändert aber die (relativen) Häufigkeiten unterscheiden sich verhältnismäßig wenig (zu sehen durch die Werte entlang der y-Achsen beider Grafiken):
> kk21.groesse <- 15469000
> wl.kk.pmw <- freq.rel(freq.absolut = wl.kk, korp.groesse = kk.groesse)
> wl.kk21.pmw <- freq.rel(freq.absolut = wl.kk21, korp.groesse = kk21.groesse)
> ylabel2 <- "Häufigkeit in pMW"
> barplot(wl.kk.pmw, names.arg = 1:length(wl.kk), cex.names = 0.7, cex.axis = 0.7, xlab = xlabel, ylab = ylabel2)
> barplot(wl.kk21.pmw, names.arg = 1:length(wl.kk21), cex.names = 0.7, cex.axis = 0.7, xlab = paste(xlabel, "21"), ylab = ylabel2)
In diesen Grafiken – sowohl in den Darstellungen mit absoluten
Häufigkeiten als auch in denen mit Häufigkeiten in pMW – scheinen
alle Wortlängen ab ca. 21 Buchstaben eine Häufigkeit von 0 zu haben. Aber
wie man in den Vektoren wl.kk und wl.kk21
überprüfen kann, gibt es absolute Häufigkeiten von deutlich über 100 bis
Wortlänge 35 im Kernkorpus und bis Wortlänge 30 im Kernkorpus 21:
> wl.kk [1] 249194 7294250 27418144 11200530 11100706 9727361 6454337 5396133
[9] 4852525 3932445 3221868 2317834 1606705 1160252 782895 546142
[17] 382466 277872 186176 129702 84877 58323 41422 25099
[25] 18221 10167 7423 3729 2399 1267 846 417
[33] 277 176 117 76 41 32 22 11
[41] 10 8 6 4 6 3 3 0
[49] 4 1 2 1 1 0 3 0
[57] 2 1 7 0 2 1 0 1
[65] 0 0 0 0 0 0 0 0
[73] 0 0 0 0 4 0 0 0
[81] 0 1 0 1 0 0 0 0
[89] 0 1
> wl.kk21 [1] 24456 885495 3398136 1564988 1419213 1201745 846764 694847 590883
[10] 473723 378665 257501 189927 135387 89557 60100 45283 31874
[19] 23228 15102 11615 7313 5097 3536 2420 1286 899
[28] 440 283 119 74 55 22 20 11 12
[37] 3 5 8 2 0 0 0 0 0
[46] 1 0 0 0 0 0 0 0 0
[55] 1 0 1 0 0 0 0 0 1
Der täuschende Eindruck in den grafischen Darstellungen ist der Skalierung der y-Achse geschuldet, die notwendig ist, um alle Häufigkeiten darzustellen, weil die Wortlängen bis ca. 21 Buchstaben fast die gesamte Summe der Häufigkeiten umfasst. Besonders auffällig dabei ist, dass die Wortlänge 3 mit großem Abstand am häufigsten auftritt – warum wohl?