> op <- par(mfrow = c(1,2))
> boxplot(hund.kk.10.einzeln, ylab = "Verteilung von \"Hund\" nach Dekade im Kernkorpus", yaxp = c(1900, 1990, 9), cex.axis = 0.8)
> boxplot(wl.kk21.einzeln, ylab = "Wortlänge in Buchstaben im Kernkorpus 21")
Tabellen und Grafiken stellen Häufigkeitsverteilungen dar, indem sie alle ermittelten Häufigkeiten abbilden. Für weitere quantitative Auswertungen ist es meistens am nützlichsten, aus der Gesamtheit der Häufigkeiten einzelne Kennzahlen zu ermitteln, die die Verteilung in verschiedener Weise charakterisieren. Solche Kennzahlen heißen Statistiken der Verteilung.
Statistiken (also die Kennzahlen) werden danach klassifiziert, welche Aspekte der Gestalt von Häufigkeitsverteilungen sie messen, d.h. quantifizieren und beleuchten. Zwei wichtige Gruppierungen von Statistiken sind die Lagemaße und die Streuungsmaße. Im Folgenden stellen wir die bekanntesten dieser Maße vor und zeigen, wie man sie mit R berechnen kann. Zuerst aber ist es notwendig, einen anderen Begriff zu erläutern, denn die Entscheidung, wann man welches Maß verwenden soll, hängt vom sogenannten Skalenniveau ab, d.h. von der Art des Merkmals, dessen Ausprägungen die Verteilung abbildet.
Ein wesentlicher Bestandteil jeder statistischen Untersuchung ist das Bestimmen von Häufigkeiten der Ausprägungen eines Merkmals oder mehrerer Merkmale der Objekte der Untersuchung (der sogenannten statistichen Einheiten). Für quantitative Analyse ist es nützlich, die Ausprägungen eines Merkmals auf Zahlen abzubilden, man kann daher sagen, dass das Merkmal gemessen wird und man spricht auch vom Maß eines Merkmals.
In der Statistik unterscheidet man anhand von mathematischen Eigenschaften vier Typen oder, wie sie üblicherweise heißen, Skalen von Merkmalen. Diese Skalen sind hierarchisch organisiert, deswegen spricht man von Skalenniveaus (manchmal auch Messniveaus):
Aufgrund der hierarchischen Struktur der Skalen können Merkmale von einer höheren auf eine niedrigere Skala heruntergestuft werden, aber nicht umgekehrt. Beispielsweise kann ein verhältnisskaliertes Merkmal wie Länge auch mit einem Ordinalskala (z.B. länger oder kürzer) oder mit einem Nominalskala (z.B. hat eine bestimmte Länge oder nicht) beschrieben werden. Aber umgekehrt geht es nicht: Es gibt z.B. zwischen Femininum, Maskulinum und Neutrum keine natürliche Rangordnung und kein mathematisch sinnvolles Intervall oder Verhältnis.
Ein statistisch interessantes Merkmal hat immer mehr als eine Ausprägung und die Ausprägungen variieren zwischen einzelnen Objekten (statistischen Einheiten) und ihre Häufigkeiten variieren zwischen verschiedenen Gruppen von Objekten. Daher heißt ein Merkmal in der Statistik auch eine Variable und eine Merkmalsausprägung heißt ein Variablenwert oder einfach Wert.
Ein Lagemaß ist ein Kennwert, der aus beobachteten Variablenwerten einer Häufigkeitsverteilung ausgewählt oder berechnet wird und als charakteristisch oder typisch für diese Häufigkeitsverteilung betrachtet wird. Weil in vielen Verteilungen dieser Kennwert in gewisser Weise der Mitte der Verteilung entspricht, heißen solche Maße auch Maße der zentralen Tendenz. Die gebräuchlichsten Lagemaße sind das arithmetische Mittel, der Median, und der Modalwert.
Der Modalwert (auch Modus genannt) einer Häufigkeitsverteilung ist der Wert, der am häufigsten auftritt.
Der Modalwert lässt sich oft direkt an der grafischen Darstellung einer Häufigkeitsverteilung erkennen: Er entspricht der längsten Säule in einem Säulendiagramm, dem Punkt ganz rechts in einem Dotplot, der größten „Schnitte“ in einem Tortendiagramm, oder dem höchsten Punkt in einem Liniendiagramm. Z.B. kann man aufgrund des Liniendiagramms der Verteilung von Hund im DWDS-Kernkorpus nach Dekade behaupten, dass diese eine bi- oder multimodale Verteilung ist.
Mit R gibt es verschiedene Möglichkeiten den Modalwert zu ermitteln.
data.frame() gebildeten und
durch order()
sortierten Häufigkeitstabelle ist der Modalwert der Wert in der
letzten bzw. ersten Zeile der Tabelle.names() mit Namen versehenen und
durch sort()
sortierten Vektor ist der Modalwert der Wert im letzten
bzw. ersten Element des Vektors.order() als
auch sort() das Argument decreasing =
TRUE.)
which.max() verwenden: Diese gibt die
numerische Position des maximalen Werts des Vektors (also hier die
Position der maximalen Häufigkeit) zusammen mit dem
„Namen“ dieses Werts aus – und der Name ist der
Modalwert der Verteilung. Hier sind Beispiele mit drei vorher
erstellten Häufigkeitsverteilungen:> which.max(dwds.hund.pmw)
Filmuntertitel
9
> which.max(hund.kk.tk.pmw)
Belletristik
1
> which.max(hund.kk.10.pmw)
1950
6
N.B.: which.max() gibt bei echten multimodalen
Verteilungen nur die Position des ersten der Modalwerte aus,
folglich kann man mit which.max() nicht bestimmen, ob
eine Verteilung multimodal ist.
Um eine Funktion in R (oder überhaupt) zu definieren, die Verteilungen
wie hund.kk.10.pmw als multimodal bezeichnen würde, obwohl
sie eigentlich nur einen einzigen tatsächlich häufigsten Wert hat,
müsste man zuerst spezifizieren, wann mehrere nicht identische Werte als
(ungefähr) gleich häufig gelten; diese Aufgabe ist aber zu kompliziert
für dieses Seminar.
Wenn alle Variablenwerte, die eine Häufigkeitsverteilung bilden, in eine Rangordnung gebracht werden können, dann kann man den Variablenwert „in der Mitte“ der Verteilung ermitteln. Dieser Wert heißt der Median: Er teilt die Verteilung in zwei gleich große Gruppen so, dass alle Werte der einen Gruppe nicht ranghöher als der Median und alle Werte der anderen Gruppe nicht rangniedriger als der Median sind. Die Anzahl der Werte macht dabei einen Unterschied:
Für dieses Lagemaß gibt es in R eine Funktion, die
auch median() heißt: Sie nimmt einen Vektor von numerischen
Werten und gibt den Median zurück. Betrachten wir als Beispiel die
schon erstellte Verteilung von Hund im DWDS-Kernkorpus nach
Dekade, hund.kk.10.pmw. Die Dekaden eines Jahrhunderts
haben eine natürliche Rangordnung, daher scheint es nahezuliegen, den
Median dieser Verteilung wie folgt zu berechnen:
> median(hund.kk.10.pmw)
[1] 31.01998
Allerdings hat das Ergebnis offensichtlich nichts mit Dekaden zu tun.
Das Problem ist, dass die Elemente des
Vektors hund.kk.10.pmw die Häufigkeiten der jeweilige
Dekaden sind, aber für die Berechnung des Medians brauchen wir den Vektor
aller Vorkommen der einzelnen Dekadenbezeichner ‚1900‘,
‚1910‘, ‚1920‘ usw.
Diesen Vektor können wir mit Hilfe der eingebauten
R-Funktion rep() und der schon
erstellten Vektoren
der Häufigkeiten von Hund nach Dekade hund.kk.10.fa
und der Dekadenbezeichner kk.10 wie folgt erstellen:
> hund.kk.10.einzeln <- rep(kk.10, times = hund.kk.10.fa)Anmerkung:
rep() (steht für replicate, also
replizieren, wiederholen) nimmt einen Vektor x als erstes Argument und
gibt einen neuen Vektor mit Wiederholungen der Elemente von x zurück.
Der Wert des Arguments times gibt die Anzahl der
Wiederholungen an: Wenn der Wert von times ein Vektor y
ist, der dieselbe Länge wie die des Vektors x hat, dann gibt jedes
Element von y die Anzahl der Wiederholungen des entsprechenden
Elements von x an.Die obige Anweisung erzeugt also einen Vektor von numerischen Dekadenbezeichner, wobei die Anzahl der Wiederholungen jedes Dekadenbezeichner (1900, 1910 usw.) gleich der absoluten Häufigkeit von Hund in der entsprechenden Dekade ist. Die ersten bzw. letzten Elemente sowie die Anzahl der Elemente dieses Vektors erhält man mit folgenden Eingaben:
> head(hund.kk.10.einzeln)
[1] 1900 1900 1900 1900 1900 1900
> tail(hund.kk.10.einzeln)
[1] 1990 1990 1990 1990 1990 1990
> length(hund.kk.10.einzeln)
[1] 4395
Anmerkung:
head() und tail()
mit nur einem Vektor als Argument auf, werden maximal die ersten
bzw. letzten sechs Elemente des Vektors ausgegeben; mit einem zweiten
Argument n, die eine ganze Zahl als Wert hat, können mehr
oder weniger Elemente des Vektors gezeigt werden.Jetzt können wir den Median der Dekaden aus der Häufigkeitsverteilung von Hund nach Dekaden ermitteln:
> median(hund.kk.10.einzeln)
[1] 1950
Anmerkung:
hund.kk.10.einzeln sind die einzelnen Werte
schon in aufsteigender Rangfolge angeordnet, weil der
Vektor kk.10 schon diese Rangfolge hat.
Die median()-Funktion berechnet den Median aber auch aus
einem unsortierten Vektor.N.B.: Das Argument von median() muss ein Vektor von Zahlen
sein, weil die Rangordnung auf einer numerischen Sortierung (und nicht
etwa auf einer alphabetischen) basiert. Um also den Median einer
Häufigkeitsverteilung von Werten einer nicht-numerischen ordinalen
Variablen (wie z.B. Grammatikalilität oder Komplexität) mit dieser
Funktion zu berechnen, muss man die Variablenwerte auf Zahlen abbilden,
einen entsprechenden Vektor von Häufigkeiten bilden und diesen Vektor
der Funktion als Argument übergeben. Wie man das machen kann, sehen wir
gleich unten.
Man mag an dieser Stelle einwenden, dass auch ‚1950‘
eigentlich gar kein Dekadenbezeichner ist: Eine Dekade ist ja eine
Spanne von 10 Jahren und 1950 bezeichnet nur ein Jahr. Und als Ausdruck
für die Dekade 1950-1959 benutzt nicht etwa „die Jahre 1950“
sondern z.B. „die 1950er Jahre“ – aber
‚1950er‘ ist keine Zahl, ist also kein gültiger Wert für
die median()-Funktion.
Ein zweites Problem zeigt folgende Berechnung in R:
> median(c(1950, 1960))
[1] 1955
‚1955‘ scheint erst recht kein Dekadenbezeichner zu sein.
Aus diesen Überlegungen lässt sich schlussfolgern, dass auch Dekadenbezeichner (wie Grammatikalilitäts- und Komplexitätsbezeichner) keine Zahlen sind sondern müssen auf Zahlen abgebildet werden, um ein Maß wie den Median zu berechnen, z.B. wie folgt:
> Dekaden <- 1:10
> hund.kk.10.einzeln2 <- rep(Dekaden, times = hund.kk.10.fa)
> head(hund.kk.10.einzeln2)
[1] 1 1 1 1 1 1
> tail(hund.kk.10.einzeln2)
[1] 10 10 10 10 10 10
> median(hund.kk.10.einzeln2)
[1] 6
Die Median-Dekade der Verteilung ist also die sechste Dekade 1950-1959 (die sechste, weil die erste Dekade ja die Jahre 1900-1909 umfasst).
Auch bei dieser Vorgehensweise bleibt das zweite Problem in anderer Form:
> median(c(6, 7))
[1] 6.5
Den Wert 6.5 zu deuten als „die Dekade zwischen der sechsten und der siebten“ erscheint eher unsinnig. Daraus könnte man den Schluss ziehen, dass Dekaden(bezeichner) zwar ordinalskalierte jedoch keine zahlenwertige Variablen sind und daher ist der Median streng genommen kein geeignetes Maß für sie. Aber abgesehen von solchen Grenzfällen scheint der Median auch bei solchen Variablen ein nützliches Lagemaß zu sein.
Während der Median die Rangfolge von numerisch darstellbaren Variablenwerten berücksichtigt, gibt es ein weiteres Lagemaß, das arithmetische Mittel, das die Werte der Variablen selbst berücksichtigt, vorausgesetzt, diese Werte sind Zahlen. Das arithmetische Mittel ist der durchschnittliche Wert einer solchen Häufigkeitsverteilung, definitionsgemäß also die Summe der einzelnen Variablenwerte geteilt durch die Gesamtanzahl dieser Werte (oder äquivalent geteilt durch die Summe der Häufigkeiten der unterschiedlichen Werte). Hier sind z.B. zwei R-Eingaben für die Häufigkeitsverteilung von Hund nach Dekade:
> sum(hund.kk.10.einzeln) / length(hund.kk.10.einzeln)
[1] 1945.374
> sum(hund.kk.10.einzeln) / sum(hund.kk.10.fa)
[1] 1945.374
Aber nicht überraschenderweise gibt es für diese Berechnung auch eine
eingebaute R-Funktion, mean() (mean bedeutet
Mittelwert):
> mean(hund.kk.10.einzeln)
[1] 1945.374
Allerdings ist 1945.374 ein noch unsinnigerer Wert als 1950 oder 6.5 für eine Dekade, was den oben gezogenen Schluss unterstreicht, dass es sich bei Dekaden nicht um Zahlen handelt. Daher brauchen wir für ein sinnvolles Beispiel des arithmetischen Mittels eine andere Häufigkeitsverteilung, und zwar von einer verhältnisskalierten Variable.
Die Eigenschaft Wortlänge ist eine Verhältnisvariable: Das
Längenverhältnis zwischen Wörtern aus einem, aus zwei, aus drei
Buchstaben usw. ist immer dasselbe Intervall, und es gibt einen
natürlichen Nullpunkt (keinen Buchstaben). Daher können wir die schon
erstellten Verteilungen wl.kk und wl.kk21
der Wortlängen im DWDS
Kernkorpus bzw. Kernkorpus 21 verwenden, um die Berechnung des
arithmetischen Mittels zu zeigen.
Allerdings sind die Elemente auch dieser Vektoren Häufigkeiten, aber
wie beim Median brauchen wir für die Berechnung des arithmetischen
Mittels den Vektor der einzelnen vorkommenden Wortlängen; diese können
wir wie oben mit Hilfe der Funktion rep() erstellen:
> (wl.kk.len <- length(wl.kk))
[1] 90
> wl.kk.einzeln <- rep(1:wl.kk.len, times = wl.kk)
> (wl.kk.einzeln.len <- length(wl.kk.einzeln))
# alternativ: sum(wl.kk)
[1] 98492552
> (wl.kk.einzeln.sum <- sum(wl.kk.einzeln))
[1] 571432675
> mean(wl.kk.einzeln)
# alternativ: wl.kk.einzeln.sum/wl.kk.einzeln.len
oder: wl.kk.einzeln.sum/sum(wl.kk)
[1] 5.801786
> (wl.kk21.len <- length(wl.kk21))
[1] 63
> wl.kk21.einzeln <- rep(1:wl.kk21.len, times = wl.kk21)
> (wl.kk21.einzeln.len <- length(wl.kk21.einzeln))
# alternativ: sum(wl.kk21)
[1] 12360098
> (wl.kk21.einzeln.sum <- sum(wl.kk21.einzeln))
[1] 70865701
> mean(wl.kk21.einzeln)
# alternativ: wl.kk21.einzeln.sum/wl.kk21.einzeln.len
oder: wl.kk21.einzeln.sum/sum(wl.kk21)
[1] 5.733425
Man merke, dass sich die arithmetischen Mittel der Wortlängen in beiden Korpora nur geringfügig unterscheiden, obwohl das Kernkorpus fast achtmal so viele Wortformen enthält wie das Kernkorpus 21 (ca. 98,5 Mio. bzw. ca. 12,4 Mio.). Dieses Maß, wie auch schon die Darstellung der Häufigkeiten in pMW, bestätigt also noch einmal die Beobachtung, dass die zwei Häufigkeitsverteilungen sehr ähnlich sind.
Ein Streuungsmaß (auch Dispersionsmaß genannt) gibt quantitativ Auskunft darüber, wie nah sich die Werte einer Häufigkeitsverteilung um das Lagemaß (den zentralen Wert) der Verteilung häufen. Eine im Verhältnis zum zentralen Wert kleine Streuung bedeutet, dass der größte Teil der Verteilung nah an diesem Mittelwert liegt, was die Annahme dieses Wertes als der typische oder charakteristische Wert der Verteilung gewissermaßen rechtfertigt. Die bekanntesten Streuungsmaße sind Spannweite, Quartile und Standardabweichung.
Die Spannweite einer Häufigkeitsverteilung ist die Differenz zwischen
dem größten und dem kleinsten Wert der Verteilung. In R lässt sie sich
mit den Funktionen range() und diff()
berechnen; range() nimmt einen Vektor von numerischen
Werten als Argument und gibt einen Vektor mit dem kleinsten und dem
größten Wert zurück und diff() berechnet die Differenz
dieser Werte:
> diff(range(hund.kk.10.einzeln))
[1] 9 # nur nach Umkodierung auf 1:10, sonst = 90
> diff(range(wl.kk21.einzeln))
[1] 62
> diff(range(wl.kk.einzeln))
[1] 89
Anmerkung:
Wenn die einzelnen Werte einer Häufigkeitsverteilung in eine aufsteigende Rangordnung gebracht und in vier Abschnitte so geteilt werden, dass jeder Abschnitt dieselbe Anzahl an Werten umfasst, dann heißen die Werte an den drei Schnittstellen die Quartile der Verteilung.
Das erste oder 25%-Quartil grenzt also das niedrigste Viertel der Werte von den drei höheren Vierteln ab, das zweite oder 50%-Quartil teilt die Werte in zwei Hälften und ist folglich identisch mit dem Median, und das dritte oder 75%-Quartil grenzt das höchste Viertel der Werte von den drei niedrigeren Vierteln ab. Die Differenz zwischen dem 75%- und dem 25%-Quartil heißt der Interquartilsabstand (auch einfach Quartilsabstand).
Gelegentlich werden auch andere Unterteilungen verwendet, z.B. Dezile (zehn Abschnitte) und Perzentile (hundert Abschnitte). Im Allgemeinen heißen die Abschnitte Quantile. Das %0-Quantil ist der kleinste Wert der Verteilung und das 100%-Quantil der größte Wert, d.h. aus diesen Quantilen ergibt sich die Spannweite der Verteilung.
Die R-Funktion quantile() nimmt einen Vektor von
numerischen Werten als Argument und gibt eine Tabelle der 0%-, 25%-,
50%-, 75%- und 100%-Quantile aus; die R-Funktion IQR() gibt
mit demselben Argument den Interquartilsabstand (IQR ist eine Abkürzung
für interquartile range) aus:
> quantile(hund.kk.10.einzeln) 0% 25% 50% 75% 100%
1 3 6 8 10 # nach Umkodierung auf 1:10, sonst = 1900 1920 1950 1970 1990
> IQR(hund.kk.10.einzeln)
[1] 5 # nach Umkodierung auf 1:10, sonst = 50
> quantile(wl.kk21.einzeln) 0% 25% 50% 75% 100%
1 3 5 7 63
> IQR(wl.kk21.einzeln)
[1] 4
> quantile(wl.kk.einzeln) 0% 25% 50% 75% 100%
1 3 5 8 90
> IQR(wl.kk.einzeln)
[1] 5
Achtung:
wl.kk.einzeln (mit
über 98 Mio. Elementen) erfordert viel Hauptspeicher im Rechner;
reicht dieser nicht aus, stürzt R ab.Die quantile()-Funktion berechnet auch Dezile, Perzentile
und anderen Quantile mit Hilfe eines zweiten
Arguments, probs, der als Wert einen Vektor von Zahlen
zwischen 0 und 1 hat, die die Anzahl der Quantile angeben; für diesen
Vektor ist die Funktion seq() nützlich, die den Startwert,
den Endwert und das Intervall zwischen den Werten als Argumente hat und
den entsprechenden Vektor erzeugt. Beispiele für Dezile und
Perzentile (mit einer verkürzten Ausgabe der Letzteren):
> quantile(wl.kk21.einzeln, probs=seq(0, 1, 0.1)) 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100%
1 3 3 3 4 5 6 7 8 11 63
> quantile(wl.kk21.einzeln, probs=seq(0, 1, 0.01)) 0% 1% 2% 3% 4% 5% 6% 7% 8% 9% 10% 11% 12% 13% 14% 15%
1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3
...
96% 97% 98% 99% 100%
13 14 15 17 63
Eine anschauliche grafische Darstellung der Quartile einer
Häufigkeitsverteilung ist der Boxplot (auch Kastengrafik
genannt), der mit der R-Funktion boxplot() erstellt werden
kann:
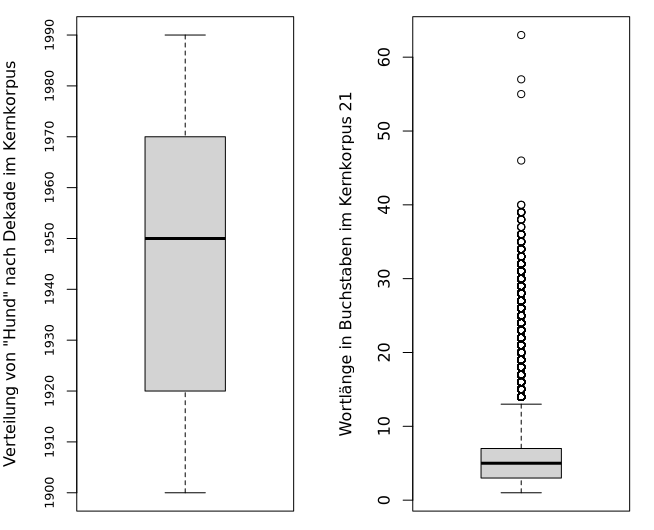
> op <- par(mfrow = c(1,2))
> boxplot(hund.kk.10.einzeln, ylab = "Verteilung von \"Hund\" nach Dekade im Kernkorpus", yaxp = c(1900, 1990, 9), cex.axis = 0.8)
> boxplot(wl.kk21.einzeln, ylab = "Wortlänge in Buchstaben im Kernkorpus 21")

Anmerkung:
wl.kk.einzeln (mit über 98 Mio. Elementen)
erfordert viel Hauptspeicher im Rechner; reicht dieser nicht aus,
stürzt R ab.Der Boxplot zeigt folgende Eigenschaften der Verteilung:
Das bekannteste und für Verhältnisvariablen gebräuchlichste Streuungsmaß ist die Standardabweichung, die wie das arithmetische Mittel (das, wie wir gleich sehen werden, bei der Berechnung der Standardabweichung auch verwendet wird) alle Variablenwerte, aus denen die Häufigkeitsverteilung gebildet wird, berücksichtigt. Die zugrundeliegende Idee dieses Maßes ist, die Streuung einer Häufigkeitsverteilung als die durchschnittliche Abweichung der einzelnen Werte vom arithmetischen Mittel der Verteilung zu behandeln; Abweichung bedeutet hier einfach die arithmetische Differenz.
Hier ist die Formel, die diese Idee mathematisch ausdrückt (Σ ist das Summenzeichen, xi stellt die einzelnen Variablenwerte dar, n die Anzahl aller Variablenwerte und x steht für das arithmetische Mittel der Verteilung):
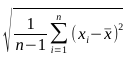
Erläuterung dieser Formel:
Diese Formel kann man direkt in R übersetzen, für unsere
Wortlängen-Beispiele wie folgt (sqrt() ist die
Quadratwurzel-Funktion (square root) und ^ der
Potenzierungsoperator, ^2 bedeutet also hoch 2, d.h. Quadrieren):
> sqrt(sum((wl.kk21.einzeln -
mean(wl.kk21.einzeln))^2)/(wl.kk21.einzeln.len - 1))
[1] 3.426251
> sqrt(sum((wl.kk.einzeln - mean(wl.kk.einzeln))^2)/(wl.kk.einzeln.len - 1))
[1] 3.502102
Aber wie man erraten kann, gibt es in R auch eine eingebaute Funktion
für die Standardabweichung, sd() (steht für standard
deviation, den englischen Namen dieses Maßes) sowie eine für die
Varianz einer Häufigkeitsverteilung, var():
> sd(wl.kk21.einzeln)
[1] 3.426251
> var(wl.kk21.einzeln) # gleich sd(wl.kk21.einzeln)^2
[1] 11.7392
> sd(wl.kk.einzeln)
[1] 3.502102
> var(wl.kk.einzeln) # gleich sd(wl.kk.einzeln)^2
[1] 12.26472
Wenn man die zentrale Tendenz oder die Streuung einer gegebenen Häufigkeitsverteilung bestimmen will, hängt die Wahl des Maßes sowohl vom Skalenniveau der Variable der Verteilung als auch von der Gestalt der Verteilung ab.