> dwds.wortverlauf(auto.kk.tab2, "Automobil")
> dwds.wortverlauf(auto.kk.tab2, "Automobil", Grafik = 2)
> dwds.wortverlauf(auto.kk.tab2, "Automobil", Grafik = 3)
Im Folgenden werden zwei Beispiele für die Auswertung in R von Datensätzen aus Suchergebnissen von DWDS detailliert vorgestellt, eines für grafische und eines für quantitative Auswertungen. Ausgangspunkt für die Beispiele ist ein Datensatz aus den Suchergebnissen (Treffern und Metadaten) der Anfrage nach dem Lemma ‚Automobil‘ im DWDS-Kernkorpus. Zunächst führen wir die Suche durch und erstellen den Datensatz:
> auto.kk.df <- dwds.data.frame(Anfrage="Automobil")
> nrow(auto.kk.df) # 733 Zeilen
> dwds.data.frame(auto.kk.df)
Nr. Datum Textklasse Quelle Treffer 1 1 1930-12-31 Wissenschaft Scheidt, Walter: Kul Denn viele Menschen, 2 2 1921-03-10 Zeitung Vossische Zeitung (M Nachdem der Schofför 3 3 1957-12-31 Gebrauchsliteratur Dillenburger, Helmut Das Zusammenspiel zw 4 4 1913-03-03 Zeitung Vossische Zeitung (A Kwiet bewohnte in de 5 5 1953-12-31 Gebrauchsliteratur Spoerl, Alexander: M Auch das Automobil i 6 6 1920-02-28 Zeitung Die Fackel [Elektron Aber er lebt, er ist
Für die Auswertungen fügen wir mit folgender R-Eingabe dem Datensatz eine neue Spalte hinzu, die Bezeichner für die Dekaden enthält, in denen die Treffer jeweils erscheinen:
> auto.kk.df$Dekade <- paste0("19", substring(auto.kk.df$Datum, 3, 3), "0er")
Anmerkungen:
substring() wird aus
jedem Datum die dritte Zahl extrahiert, die die Dekade kennzeichnet
(z.B. wird aus "1957-12-31" "5" extrahiert).paste0() wird aus diesen Zahlen
Dekadenbezeichner erstellt (also aus "5" "1950er", usw.).Jetzt machen wir die neue Spalte zur 1. Spalte des Datensatzes und löschen die Nr.- und Datum-Spalten, weil wir diese nicht mehr brauchen, und zeigen das Ergebnis:
> auto.kk.df <- auto.kk.df[c(6,3:5)]
> dwds.data.frame(auto.kk.df, Abbrev = 25)
Dekade Textklasse Quelle Treffer 1 1930er Wissenschaft Scheidt, Walter: Kulturbi Denn viele Menschen, die 2 1920er Zeitung Vossische Zeitung (Morgen Nachdem der Schofför und 3 1950er Gebrauchsliteratur Dillenburger, Helmut: Das Das Zusammenspiel zwische 4 1910er Zeitung Vossische Zeitung (Abend- Kwiet bewohnte in der Huf 5 1950er Gebrauchsliteratur Spoerl, Alexander: Mit de Auch das Automobil ist ei 6 1920er Zeitung Die Fackel [Elektronische Aber er lebt, er ist da,
Das DWDS-Abfragesystem verfügt über ein statistisches Werkzeug namens Wortverlaufskurven, das den zeitlichen Verlauf (jährlich sowie nach Dekade) eines Suchbegriffs in einer Auswahl aggregierter DWDS-Korpora sowohl nach Textklasse als auch insgesamt und unter Berücksichtigung verschiedener statistischen Einstellungen grafisch darstellt. Das Werkzeug erstellt nur Liniendiagramme und nur in aggregierten Korpora. In einer früheren Version dieses Werkzeugs konnte man zwischen zwei verschiedenen Säulendiagrammen und einem mehrfachen Liniendiagramm wählen, allerdings nur nach Dekade und Textklasse und beschränkt auf das Kernkorpus. Wir zeigen hier, wie man diese (etwas einfacheren) Darstellungen für den oben erstellten Datensatz des Lemmas ‚Automobil‘ im Kernkorpus in R nachmachen kann.
Dafür benötigen wir eine Häufigkeitsverteilung des Suchbegriffs
gleichzeitig gruppiert nach Dekade und Textklasse. Solche
Häufigkeitsverteilungen, die alle Kombinationen der Werte von zwei
Variablen enthalten, kommen sehr oft in statistischen Untersuchungen vor
und in tabellarischer Form heißen sie Kontingenztafeln. In R
können wir Kontingenztafeln mit der Funktion table()
bilden. Die Argumente dieser Funktion sind Vektoren der Werte aus den
entsprechenden Spalten des Datensatzes:
> (auto.kk.tab <- with(auto.kk.df, table(Textklasse, Dekade)))
Dekade
Textklasse 1900er 1910er 1920er 1930er 1940er 1950er 1960er 1970er
Belletristik 22 42 25 3 4 10 2 5
Gebrauchsliteratur 19 20 43 8 4 100 6 6
Wissenschaft 2 1 0 3 5 1 2 3
Zeitung 102 117 86 31 7 6 0 6
Dekade
Textklasse 1980er 1990er
Belletristik 1 0
Gebrauchsliteratur 6 20
Wissenschaft 4 2
Zeitung 3 6
table()
bestimmt die Gruppierungen der Kontingenztafel und folglich die
tabellarischen und grafischen Darstellungen. Eine
mit table(Dekade, Textklasse) erstellte Kontingenztafel
stellt zwar diesselbe Verteilung dar, wäre aber weniger übersichtlich
(versuchen Sie es!).Für die grafischen Darstellungen verwenden wir die
Funktionen barplot() und plot(), jeweils mit
dem Argument col, um die Verteilungen farblich zu
unterscheiden. Die zwei Säulendiagramme werden durch das
Argument beside unterschieden: Mit dem voreingestellten
Wert FALSE werden die Säulen der Textklassen in jeder
Dekade gestapelt, wodurch die Gesamthäufigkeit pro Dekade deutlich wird;
mit dem Wert TRUE werden die Säulen der Textklassen in
jeder Dekade nebeneinander dargestellt, wodurch der direkte Vergleich
zwischen den Textklassen erleichtert wird:
> farben <- hcl.colors(4, palette="Dark 3")
> barplot(auto.kk.tab, col=farben)
> barplot(auto.kk.tab, beside=TRUE, col=farben)
hcl.colors() erzeugt
wie rainbow()
einen Vektor von Farbnamen, die nach einem Farbschema ausgewählt sind,
das durch das Argument palette angegeben ist. Die Farben
sind nicht so grell wie die von rainbow() erzeugten
Farben. Eine Liste der vielen Farbschemas erhalten Sie durch Aufruf
der Funktion hcl.pals(), damit können Sie verschiedene
Farbkombinationen mit hcl.colors() ausprobieren.Für das mehrfache Liniendiagramm ist es sinvoll, nicht nur ein
Liniendiagramm pro Textklasse zu erstellen sondern auch noch eines für
das gesamte Korpus, was praktisch den Darstellungen beider
Säulendiagramme zusammen entspricht. Die Werte für das Gesamtkorpus
sind die Summen der Werte pro Dekade, also der Spalten der oben
erstellten Kontingenztafel, die man mithilfe der
Funktion addmargins() erhalten kann:
> auto.kk.tab2 <- addmargins(auto.kk.tab)
> auto.kk.tab2[ , 1:10]
Dekade
Textklasse 1900er 1910er 1920er 1930er 1940er 1950er 1960er 1970er
Belletristik 22 42 25 3 4 10 2 5
Gebrauchsliteratur 19 20 43 8 4 100 6 6
Wissenschaft 2 1 0 3 5 1 2 3
Zeitung 102 117 86 31 7 6 0 6
Sum 145 180 154 45 20 117 10 20
Dekade
Textklasse 1980er 1990er
Belletristik 1 0
Gebrauchsliteratur 6 20
Wissenschaft 4 2
Zeitung 3 6
Sum 14 28
addmargins() erzeugt
eine weitere Spalte, die die Summen der Zeilen sowie die Gesamtsumme
der Zeilen und Spalten enthält, die wir aber hier nicht benötigen.
(Wir werden uns im letzten Themenblock des Seminars wieder
mit addmargins() beschäftigen.)Damit alle Liniendiagramme auf dieselbe grafische Fläche passen, muss
man zuerst das Diagramm mit dem größten Wert der Häufigkeitstabelle
erstellen, also das Liniendiagramm für das Gesamtkorpus. Das kann man
mit plot() machen und anschließend die übrigen Diagramme
mit der Funktion points() hinzufügen (weil
weitere plot()-Aufrufe bestehende Grafiken löschen
würden):
> farben <- hcl.colors(5, palette="Dark 3")
> plot(auto.kk.tab2[5 , 1:10], type="b", col=farben[5])
> points(auto.kk.tab2[1, 1:10], type="b", col=farben[1])
> points(auto.kk.tab2[2, 1:10], type="b", col=farben[2])
> points(auto.kk.tab2[3, 1:10], type="b", col=farben[3])
> points(auto.kk.tab2[4, 1:10], type="b", col=farben[4])
Wenn Sie alle der vorangehenden Anweisungen zur Erstellung der drei
Verlaufsdiagramme in R eingeben, werden Sie sehen, dass die
resultierende Grafiken ziemlich minimalistisch sind, ohne schöne und
informative Beschriftungen. Außerdem ist es mühsam, diese Anweisungen
für andere Kontingenztafeln jedes Mal einzeln einzugeben. Daher, um die
Erstellung solcher Grafiken auch mit anderen Suchbegriffen zu
erleichtern, haben wir eine R-Funktion
definiert: dwds.wortverlauf() (die wie gehabt mit
dem
source-Aufruf
in R geladen wird). Diese Funktion nimmt fünf Argumente, die ersten
zwei sind obligatorisch und die übrigen optional (weil sie
voreingestellte Werte haben):
auto.kk.tab in dem Beispiel. (Der Wert kann auch
eine Kontingenztafel mit Spaltensummen, wie auto.kk.tab2,
aber diese sind nicht erforderlich.)Grafik hat als Wert eine der Zahlen
1, 2 oder 3. Mit Grafik = 1 wird ein Säulendiagramm mit
gestapelten Säulen, mit Grafik = 2 ein Diagram mit
Säulengruppen und mit Grafik = 3 Liniendiagramme
erstellt.Farben hat als Wert einen Vektor
von 5 Farbnamen. Die Namen können Sie z.B. aus der durch Aufruf
von colors() ausgebenen Liste auswählen und mit
der c() übergeben, oder auch die
Funktionen rainbow() oder hcl.colors() wie
oben beschrieben verwenden.hcl.colors(5, palette = "Dark 3").
legend.pos hat als Wert eine Zahl.
Mit legend.pos=1 wird eine Legende für die Farben in die
obere rechte Ecke der grafischen Fläche plaziert.
Mit legend.pos=2 wird die Legende dorthin platziert, wo
Sie mit der Maus auf der grafischen Fläche klicken (nützlich für den
Fall, dass Säulen oder Linien in der oberen rechten Ecke sind, sodass
die Legende woanders hin muss).dwds.wortverlauf()
funktioniert korrekt nur für Suchergebnisse aus dem DWDS-Kernkorpus,
weil sie nur die vier Textklassen und zehn Dekaden aus diesem Korpus
berücksichtigt (wobei es egal ist, ob es in jeder Textklasse und jeder
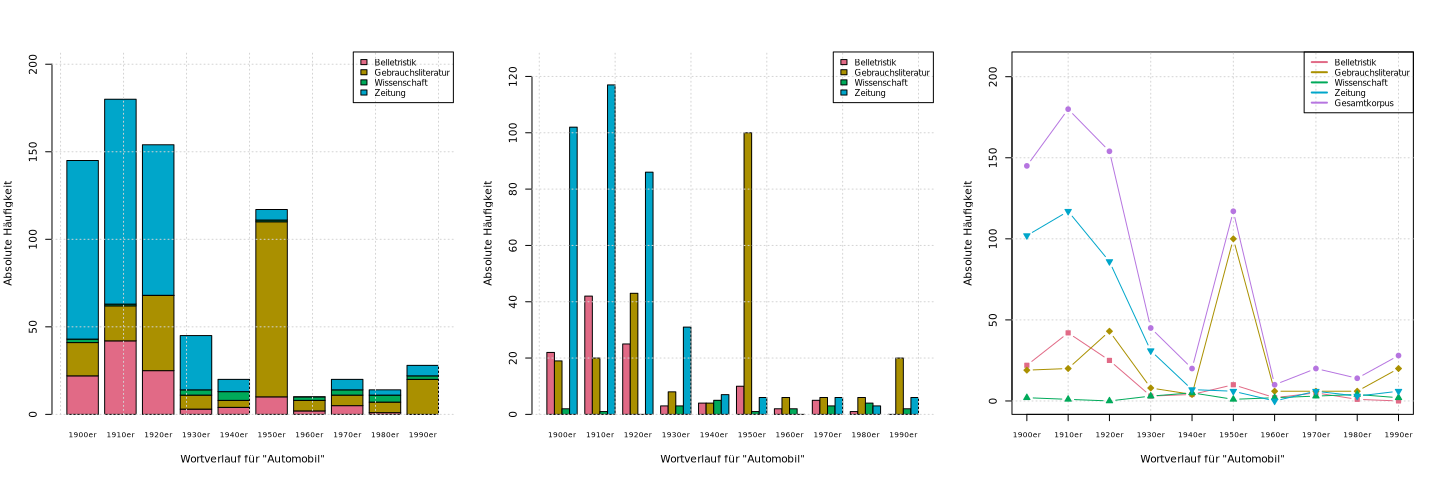
Dekade tatsächlich Treffer gibt).Die Funktion erstellt auch automatisch passende Beschriftungen der x-
und y-Achse sowie einen Raster auf der grafischen Fläche, um die
Häufigkeiten besser ablesen zu können. Hier sind drei Aufrufe dieser
Funktion und die damit erzeugten Grafiken für Häufigkeitsverteilungen
des Lemmas ‚Automobil‘ (wenn Sie die Grafiken gleichzeitig
in je einem Fenster sehen wollen, rufen Sie dev.new() vor
dem zweiten und dritten Aufruf auf):
> dwds.wortverlauf(auto.kk.tab2, "Automobil")
> dwds.wortverlauf(auto.kk.tab2, "Automobil", Grafik = 2)
> dwds.wortverlauf(auto.kk.tab2, "Automobil", Grafik = 3)

Als zweites Beispiel zeigen wir, wie man verschiedene Lage- und
Streuungsmaße von einzelnen und gruppierten Häufigkeitsverteilungen aus
Datensätzen berechnen kann. Ausgangspunkt hier sind die Längen in
Zeichen (eine Verhältnisvariable) der Treffer in unserem
Auto-Datensatz auto.kk.df; diese Längen ermitteln wir mit
die R-Funktion nchar() (wir könnten den sich ergebenden
Vektor dem Datensatz als neue Spalte hinzufügen, wie wir es oben mit der
Variable Dekade gemacht haben, aber das wäre für dieses Beispiel ein
unnötiger Aufwand, daher belassen wir es beim Vektor):
> treffer.laengen <- nchar(auto.kk.df$Treffer)
Die Spannweite können wir mit range()
und diff() wie
vorher berechnen, oder alternativ auch, indem wir den längsten und
den kürzesten Treffer mit den Funktionen max()
und min() ermitteln:
> (tl.max <- max(treffer.laengen))
[1] 11213
> (tl.min <- min(treffer.laengen))
[1] 17
> tl.max - tl.min # Spannweite, = diff(range(treffer.laengen))
[1] 11196
Für den Modalwert der Trefferlängen müssen wir eine Häufigkeitstabelle
der Trefferlängen erstellen und können
dann wie schon
gesehen die Funktion which.max() verwenden:
> tl.tab <- table(treffer.laengen)
> which.max(tl.tab)
139
102
Demnach wäre der Modalwert die Trefferlänge 139 (die
„Namen“ der Trefferlängen sind einfach die jeweiligen
Zahlen), die das 102. Element der Häufigkeitstabelle ist. Wir haben
aber schon
darauf hingewiesen,
dass, wenn die Verteilung mehr als einen häufigsten Wert
hat, which.max() nur den ersten ausgibt. Um das zu
überprüfen, können wir mit max() die größte Häufigkeit
ermitteln und mit which() herausfinden, ob es mehrere Werte
mit dieser Häufigkeit gibt:
> max(tl.tab)
[1] 8
> which(tl.tab == max(tl.tab))
139 163
102 126
Die maximale Häufigkeit der Trefferlängen ist also 8, aber wie wir sehen, weisen zwei verschiedene Längen diese Häufigkeit auf: 139 und 163. Demnach handelt es sich eigentlich um eine bimodale Verteilung.
Für die übrigen Lage- und Streuungsmaße brauchen wir nur den Vektor der Trefferlängen:
> median(treffer.laengen)
[1] 163
> quantile(treffer.laengen)
0% 25% 50% 75% 100%
17 112 163 239 11213
> IQR(treffer.laengen)
[1] 127
> mean(treffer.laengen)
[1] 221.337
> sd(treffer.laengen)
[1] 587.8542
Diese Ergebnisse deuten auf eine sehr schiefe Häufigkeitsverteilung der Trefferlängen hin, und grafische Darstellungen bestätigen das:
> dev.new(width=15, height=5)
> plot(tl.tab, type="p", xlab="Trefferlängen", ylab="Häufigkeit")

> dev.new(width=15, height=3)
> boxplot(treffer.laengen, horizontal = TRUE, xlab="Trefferlängen")

Der längste Treffer ist offenbar ein extremer Ausreißer – oder
vielmehr, wie der plot()-Aufruf grafisch bestätigt, handelt
es sich um zwei gleichwertige extreme Ausreißer. Und diese Grafik zeigt
auch, dass auch die zweitlängste Trefferlänge zweimal vorkommt. Eine
numerische Bestätigung der grafischen Beobachtungen gibt die folgende
R-Anweisung, die die sechs größten Trefferlängen ausgibt:
> head(sort(treffer.laengen, decreasing=TRUE))
[1] 11213 11213 867 867 787 766
Diese zwei wiederholten Längen muten seltsam an. Aber es stellt sich heraus, dass es sich bei diesen vier längsten Treffern lediglich um zwei Sätze handelt, die beide in den Suchergebnissen zweimal vorkommen, wie folgende R-Eingaben beweisen:
# An welchen Positionen des Vektors treffer.laengen sind die zwei längsten Trefferlängen?
# (N.B.: Da beim Export aus DWDS die Treffer zufällig sortiert waren, werden die Werte
# bei Wiederholungen dieses Beispiels wahrscheinlich an anderen Positionen sein.)
> which(treffer.laengen == 11213)
[1] 270 491
> which(treffer.laengen == 867)
[1] 123 181
# Sind die je zwei Vorkommen dieser Trefferlängen identische Treffer,
# d.h. handelt es sich wirklich nur um zwei unterschiedliche Sätze?
> auto.kk.df$Treffer[c(270, 123)] == auto.kk.df$Treffer[c(491, 181)]
[1] TRUE TRUE # Ja, sie sind identisch!
Warum gibt es mehr als einen Treffer desselben Satzes (bzw. derselben zwei Sätze)? Das liegt daran, dass in DWDS die absolute Häufigkeit eines Suchbegriffs mit der Anzahl der Treffer gleichgesetzt wird und als Treffer zählen komplette Sätze. Folglich, wenn der Suchbegriff mehr als einmal im selben Satz vorkommt, soll dieser Satz so oft als Treffer in DWDS erscheinen, wie es Vorkommen des Suchbegriffs im Satz gibt. Das ist für die Berechnung der absoluten Häufigkeit des Suchbegriffs nützlich aber für die Berechnung bestimmter Lage- und Streuungsmaße eines Merkmals wie Satzlänge problematisch, wie wir gleich sehen werden.
Es gibt allerdings in DWDS die Möglichkeit, die wiederholte Anzeige eines Treffersatzes zu unterbinden: Bei der Eingabe des Suchbegriffs hängt man am Ende der Anfrage das Schlüsselwort ‚#JOIN‘ dran (siehe hierzu die DWDS-Hilfeseite zu Korpussuche). Z.B. zeigt DWDS als Ergebnis der Sucheingabe ‚Automobil #JOIN‘ 722 Treffer (783 insgesamt) an, im Gegensatz zu 733 Treffer (794 insgesamt) bei der Sucheingabe ‚Automobil‘. Das Ergebnis einer „normalen“ Suche mit diesem Suchbegriff enthält also 11 wiederholte Treffersätze.
Auch in R gibt es die Möglichkeit, aus DWDS exportierte Datensätze so
zu verarbeiten, dass Wiederholungen von Treffersätzen nicht gezählt
werden: die eingebaute Funktion unique() ignoriert alle
Wiederholungen von identischen Elementen eines Vektors oder eines
Datensatzes:
> length(unique(auto.kk.df$Treffer))
[1] 722
> nrow(unique(auto.kk.df))
[1] 722
nrow() muss man allerdings vorsichtig sein, denn
bei Datensätzen sind zwei Zeilen nur dann identisch, wenn jede Zelle
der entsprechenden Spalten den identischen Inhalt hat. In unserem
Datensatz auto.kk.df ist das offenbar der Fall, aber nur
deswegen, weil wir ganz am Anfang die Nr.-Spalte entfernt haben
– sonst hätte ja jede Zeile eine andere Nummer und damit gäbe es
keine Wiederholungen von Zeilen. Es könnte jedoch auch exportierte
Datensätze geben, in denen Treffer wiederholt werden aber z.B. die
Inhalte der Quelle-Spalte der entsprechenden Zeilen nicht identisch
sind (weil z.B. die Treffer aus unterschiedlichen Zeitungen oder
Ausgaben stammen). Dann wären die Ausgaben der obigen Eingaben
unterschiedlich. Daher, wenn man sich nur für Wiederholungen von
Treffern interessiert, empfiehlt es sich, unique() nur
auf die Treffer-Spalte anzuwenden, nicht auf den ganzen Datensatz.
(Am Anfang des nächsten Abschnitts dieser Seite zeigen wir aber eine
Alternative für die Entfernung von Wiederholungen, die auch
unproblematisch auf einen ganzen Datensatz angewandt werden
kann.)Die Auswirkungen von Wiederholungen für die Berechnungen von Lage- und Streuungsmaßen in diesem Datensatz zeigt ein Vergleich der Berechnungen mit und ohne Wiederholungen:
> treffer.laengen2 <- nchar(unique(auto.kk.df$Treffer))
# Lage- und Streuungsmaßen ohne Wiederholungen:
> tl.tab2 <- table(treffer.laengen2)
> which.max(tl.tab2)
139
102
> max(tl.tab2)
[1] 8
> which(tl.tab2 == max(tl.tab2))
139 163
102 126
> diff(range(treffer.laengen2))
[1] 11196
> median(treffer.laengen2)
[1] 163
> quantile(treffer.laengen2)
0% 25% 50% 75% 100%
17.00 112.25 163.00 238.00 11213.00
> IQR(treffer.laengen2)
[1] 125.75
> mean(treffer.laengen2)
[1] 205.3324
> sd(treffer.laengen2)
[1] 426.8008
Ohne Treffer-Wiederholungen bleiben der Modalwert, die Feststelling einer bimodalen Verteilung, die Spannweite und der Median unverändert, und das 1. und das 3. Quartil, und damit der Interquartilsabstand, sind nur geringfügig kleiner als die entsprechenden Werte mit Wiederholungen. Dagegen sind das arithmetische Mittel und die Standardabweichung deutlich kleiner als die Werte dieser Maße mit Wiederholungen. Mit einem anderen Datensatz könnten die Daten so sein, dass auch die anderen Maße unterschiedliche Werte mit und ohne Wiederholungen haben, wenn es genug Wiederholungen mit Werten gibt, die diese Maße beinflussen.
Auch ohne die wiederholten Sätze bleibt die Gestalt der
Häufigkeitsverteilung fast unverändert, wie man sehen kann, wenn man
grafische Darstellungen wie die obigen mit treffer.laengen2
und tl.tab2 erstellt. Das liegt an der extremen Länge des
längsten Satzes. Wenn man entsprechende Häufigkeitsverteilungen in
vielen anderen Korpora erstellt und dabei feststellt, dass solche
extreme Ausreißer selten vorkommen, kann man sie als statistische
Anomalien betrachten und damit als nicht repräsentativ für die wirkliche
Verteilung in der Sprache. Dementsprechend könnte es aufschlussreich
sein die Verteilung, die Lage- und Streuungsmaße sowie grafische
Darstellungen ohne diesen Ausreißer zu erstellen. Den Effekt dieser
Überlegung für unser Beispiel zeigen folgende Ein- und Ausgaben in
R:
# Den extremen Ausreißer entfernen:
> treffer.laengen3 <- treffer.laengen2[-which.max(treffer.laengen2)]
> tl.tab3 <- table(treffer.laengen3)
> which(tl.tab3 == max(tl.tab3))
139 163
102 126
> diff(range(treffer.laengen3))
[1] 850
> median(treffer.laengen3)
[1] 163
> quantile(treffer.laengen3) 0% 25% 50% 75% 100%
17 112 163 238 867
> IQR(treffer.laengen3)
[1] 126
> mean(treffer.laengen3)
[1] 190.0652
> sd(treffer.laengen3)
[1] 117.85
> plot(tl.tab3, type="p", xlab="Trefferlängen", ylab="Häufigkeit")
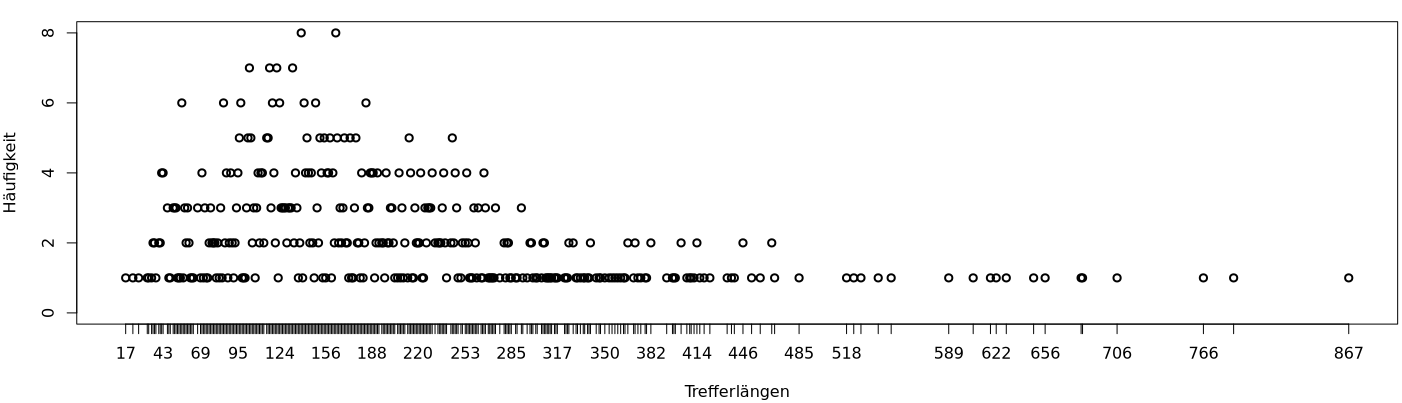
> boxplot(treffer.laengen3, horizontal = TRUE, xlab="Trefferlängen")

Es ist zwar immer noch eine sehr schiefe Häufigkeitsverteilung aber bei weitem nicht so extrem wie vorher. Und es fällt auch hier auf, dass die Modalwerte und der Median immer noch diesselben sind, und auch der Interquartilsabstand kaum verändert bleibt, aber die Spannweite, das arithmetische Mittel und die Standardabweichung jetzt sehr viel kleiner sind.
Die bisher berechneten Lage- und Streuungsmaße beziehen sich auf den ganzen Datensatz, aber kann interessant und aufschlussreich sein, Statistiken auch bezüglich der verschiedenen Ausprägungen von Datensatzmerkmalen zu berechnen, z.B. der Textklassen und der Dekaden.
Zuerst sollten wir aber die wiederholten Sätze aus dem Datensatz
entfernen, weil es ja immer noch um Statistiken von Satzlängen geht.
Weil wir oben gesehen haben, dass es in unserem
Datensatz bei Wiederholungen in der Treffer-Spalte auch Wiederholungen
in den entsprechenden Zellen der anderen Spalten gibt, genügt folgende
Eingabe zum Entfernen der Wiederholungen, wie die Ausgabe
von nrow() nochmals bestätigt:
> auto.kk.df2 <- unique(auto.kk.df)
> nrow(auto.kk.df2)
[1] 722
duplicated() die gewünschte Entfernung aller
Wiederholungen in der Treffer-Spalte wie folgt erreichen:
> auto.kk.df3 <- auto.kk.df[-which(duplicated(auto.kk.df$Treffer)), ]
> nrow(auto.kk.df3)
[1] 722
Jetzt können wir z.B. das arithmetische Mittel der Trefferlängen in Bezug auf Textklasse mit Hilfe von Indizierung ermitteln:
> mean(nchar(auto.kk.df2[auto.kk.df2$Textklasse == "Belletristik", ]$Treffer))
[1] 316.7928
> mean(nchar(auto.kk.df2[auto.kk.df2$Textklasse == "Gebrauchsliteratur", ]$Treffer))
[1] 184.3348
> mean(nchar(auto.kk.df2[auto.kk.df2$Textklasse == "Wissenschaft", ]$Treffer))
[1] 224.6087
> mean(nchar(auto.kk.df2[auto.kk.df2$Textklasse == "Zeitung", ]$Treffer))
[1] 183.0251
Diese Vorgehensweise ist zugegebenermaßen umständlich, umso mehr, wenn
wir z.B. das arithmetische Mittel der Trefferlängen in Bezug auf Dekade
berechnen wollen (dann bräuchten wir 10 Berechnungen). Aber R bietet
eine viel einfachere Möglichkeit Kennzahlen zu gruppieren, und zwar mit
der Funktion tapply():
> with(auto.kk.df2, tapply(nchar(Treffer), Textklasse, mean)) Belletristik Gebrauchsliteratur Wissenschaft Zeitung
316.7928 184.3348 224.6087 183.0251
> with(auto.kk.df2, tapply(nchar(Treffer), Dekade, mean)) 1900er 1910er 1920er 1930er 1940er 1950er 1960er 1970er
164.4357 186.1243 209.0592 207.7333 167.6000 188.4957 1397.4444 223.2000
1980er 1990er
221.5000 200.4286
Das erste Argument von tapply() ist ein Vektor, auf dem eine
Berechnung durchgeführt werden soll; das zweite Argument bestimmt die
Gruppierung der Ergebnisse; und das dritte Argument ist die Funktion,
die die Berechnung macht.
Man kann mit tapply() auch mehrfache Gruppierungen machen;
dann muss das zweite Argument eine Liste sein, die mit der
Funktion list() gebildet wird:
> with(auto.kk.df2, tapply(nchar(Treffer), list(Dekade, Textklasse), mean))
Belletristik Gebrauchsliteratur Wissenschaft Zeitung 1900er 159.8182 133.4118 130.5000 171.4747 1910er 231.6341 172.1000 177.0000 172.4174 1920er 276.8333 206.7209 NA 191.1059 1930er 104.0000 182.3750 380.3333 207.6129 1940er 157.5000 182.2500 117.8000 200.5714 1950er 185.3000 181.7100 196.0000 305.6667 1960er 11213.0000 151.8333 226.5000 NA 1970er 225.2000 182.1667 315.0000 216.6667 1980er 373.0000 186.5000 247.2500 206.6667 1990er NA 215.8000 207.5000 146.8333
Die Einträge ‚NA‘ in der Kontingenztafel bedeuten, dass es für den Suchbegriff keine Treffer mit diesen Kombinationen von Textklasse und Dekade (also Belletristik und 1990er, Wissenschaft und 1920er, Zeitung und 1960er) im Korpus gibt.