Important for the efficiency of the simulation is that the PRESS dynamics, though incorporating spatial effects, is given by a set of ordinary differential equations describing a single cavity instead of the numerically much harder to deal with partial differential equations conventionally employed in spatially non-homogeneous simulations.
The advantage of this simplex topology for describing continuous space is that it allows statistical correlations between local sites to be handled probabilistically in a self-consistent manner without having to compute higher order correlations induced by extended patterns. The approximation for can be extended to next higher order by placing pairs of cavities in the self-consistent environment of a simplex of other cavity pairs. Mathematically, this means that the equilibrium states, for example, can be explored invoking tractable self-consistency conditions. Furthermore, on a simplex, simple diffusive processes are exactly described by a mean field approach.
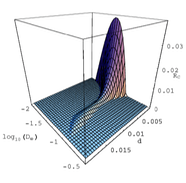
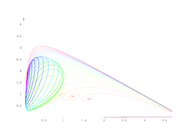
A main application of PRESS, made possible by its computational efficiency, is to explore parameter space. We applied PRESS to different problems, see [2] and [3] and aspects of [4]. Despite the fact that it seems to be a rather drastic simplification making it very efficient, we observed it to be in surprisingly good agreement with full 3D Monte Carlo simulations.