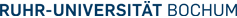PRESS local states
PRESS space
Initially presented in [1], the PRESS approach (Probability Reduced Evolution of Spatially discrete Species) incorporates relevant aspects of spatially resolved kinetics in a numerically and in important special cases even analytically tractable manner.
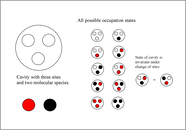
The PRESS-approach models the interactions of an infinite number of cavities, each pair of them connected, in mathematical terms this is an infinite-dimensional simplex. A cavity is so small that it can only host a limited number N of molecules.
Despite the fact that a high-dimensional simplex may look abstract, it is equivalent statistically to a large number of small chemically active cavities all connected to a large well-mixed pool in which replication processes are prevented (e.g. by dilution or absent resources). This is also the topology for viral particles proliferating in a static cell population, with rapid dispersal between cells. On the macroscale, the topology is the same as Wright’s island model of species evolution.
The finiteness of the cavities means that they only can be in a finite number of different states (depending on their size and the number of molecular species involved). The (Markovian) dynamics is then characterized by probabilistic transitions between different states, reflecting either reactions or molecular exchange between cavities.