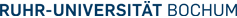Multipole forces

A: The monopole forces between two membrane particles. Short range repulsion and intermediate range attraction lead, together with the dipole-interactions, to a stable membrane. B: Angular quantities used in the definition of the dipole-potentials for curved membranes.
Conventional DPD is based on structure-less point particles, i.e. particles that are completely determined by their position, apart from scalar properties such as mass. Such particles interact with their environment (i.e. with other particles) only through radially symmetric interactions, which means that the forces (whether conservative, dissipative or random) depend only on their mutual distance, and show no further dependencies on position coordinates. The problem is that, by tailoring such forces, it is not directly possible to self-organize extended flat structures, as would be necessary for the implementation of membranes for example. The reason is that the elements forming a surface have to be capable of relatively free movements within the surface but must resist movements that would lead to a strong bending of the surface.
The classic solution is to introduce “chain-particles”, i.e. DPD-particles that are connected with stiff springs and which exhibit a three-body angular potential between three successive particles in the chain. The solution that we are pursuing is rather to replace the structureless point particles of conventional DPD by particles carrying additional multipole moments. A dipole moment can be understood just as a vector defining a direction with a certain magnitude, corresponding to particles such as amphiphiles with a preferred direction (head and tail). This interpretation of dipoles establishes a connection with chain particles. The dipole moment can be envisaged as an orientation vector that rotates but does not change its length (which we then set to one). As a result, each particle carries an angular velocity and an angular momentum vector besides its velocity and linear momentum.
The membrane forming particles are represented as multipole expansions usually truncated at the dipole term and their interactions are governed by a Lagrangian that is chosen in such a way that it exhibits the same symmetries as the membranes one wants to study. The configurations we look for are given by dipole moments aligned in parallel and perpendicular to the lines connecting two particles. These connecting lines form a surface, when understood as a virtual mesh.